通过对抗数据扩增泛化到未知域( 三 ) 摘要我们关注的学习模型可以

【通过对抗数据扩增泛化到未知域】语义场景分割我们使用 SYTHIA [31]数据集进行语义分割。数据集包含来自不同位置的图像（我们使用高速公路，类似纽约的城市和欧洲老城），以及不同的天气/时间/日期条件（我们使用黎明，雾，夜，春和冬。在源上训练模型）领域并在其他领域进行测试，使用标准平均联合交叉口（mIoU）指标来评估我们的性能[8] 。在整个实验过程中，我们从左前摄像头中任意选择了图像。对于每一个图像，我们随机抽取 900 张图像（调整大小）到 192×320 像素），我们使用具有 ResNet-50 [11]主体的完全卷积网络（FCN）[23] ，并设置超参数 α= 0.0001 ， η= 2.0 ， Tmin = 500 和 Tmax = 50.在最小化阶段，我们使用批次大小等于 8 的 Adam [17] 。将我们的方法与 ERM 基准进行比较。
4.1. 数字分类结果在本节中，我们介绍并讨论数字分类实验的结果。首先，我们对分析我们施加的语义约束的作用感兴趣。图 1a（顶部）显示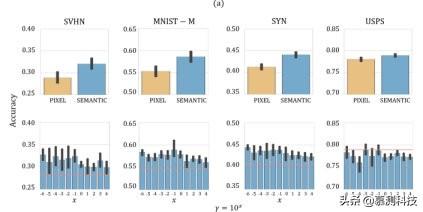
文章插图
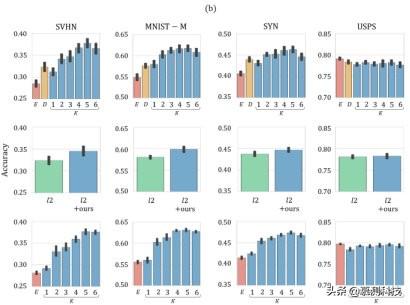文章插图
图 1.与用 10 ， 000 MNIST 样本训练并在 SVHN ， MNIST-M ， SYN 和 USPS（分别为第一栏，第二栏，第三栏和第四栏）上测试的模型相关的结果。面板（a），顶部：像素空间（黄色）和语义空间（蓝色），其中 γ= 104 且 K =1 。面板（a），底部：比较我们的 K = 2 和不同 γ 值的方法（蓝色条）和 ERM（红线））。面板（b），顶部：γ= 1.0 与不同迭代次数 K（蓝色）， ERM（红色）和 Dropout [35]（黄色）之间的比较。面板（b），中间：用 ridge（绿色）和 ridge +我们的方法（γ= 1.0 和 K = 1（蓝色））规范化的模型之间的比较。面板（b），底部：使用模型的与整体方法有关的结果使用我们的方法进行了训练，迭代次数 K 不同（蓝色），并且使用通过 ERM 训练的模型（红色）。报告的结果是通过平均 10 多次不同的运行获得的；黑条表示跨度精度范围。
与用算法 1 训练的模型具有 K = 1 和 γ= 104 关联的模型的性能，在语义空间（如第 2 节所述）和像素空间[34]（分别为蓝色和黄色条）中具有约束。图 1a（底部）显示了使用我们的方法训练的模型的性能，其中使用了不同的超参数 γ 值（K = 2）和 ERM（分别为蓝色条和红色线）。这些图显示了（i）在模型在未知域上进行测试时，移动语义空间上的约束会带来好处；（ii）在样本外域上，对于任何 γ 值，使用算法 1 胜过模型训练的模型都使用 ERM 进行训练（SVHN ， MNIST-M 和 SYN）。后一个结果是相当理想的成就，因为该超参数无法正确地交叉验证。在 USPS 上，我们的方法会导致准确性下降，因为 MNIST 和 USPS 是非常相似的数据集，因此我们的算法在训练过程中不会探索 USPS 所属的图像域，从而优化了最坏情况下的性能。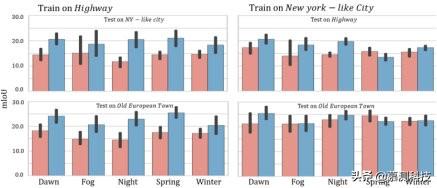
文章插图
图 2.使用 ERM 训练的语义分割模型（红色）和 K = 1 且 γ= 1.0（蓝色）的方法获得的结果。最左边的面板与在 Highway 上训练的模型相关联，最右边的面板与在类似纽约的城市上训练的模型相关联。测试数据集是公路，纽约市和欧洲古城。
图 1b（顶部）报告了与用我们的方法训练的模型相关的结果（蓝色条），改变了迭代次数 K 并固定 γ= 1.0 ，结果与 ERM（红色条）和 Dropout [35]（黄色条）相关。我们观察到，我们的方法改善了 SVHN ， MNIST-M 和 SYN 的性能，在统计上显着优于 ERM 和 Dropout [35] 。在图 1b（中）中，我们比较了用岭正则化训练的模型（绿色条）与用算法 1（K = 1 和 γ= 1.0）和岭正则化训练的模型（蓝色条）进行比较。这些结果表明，我们的方法可能会从其他正则化方法中受益，因为在这种情况下，我们观察到了两种效果的总和。我们在附录 B 中进一步报告了我们的方法与非监督域自适应算法（ADDA [39]）之间的比较，以及与超参数 γ 和 K 的不同值相关的结果。
最后，我们报告通过学习模型集成获得的结果。由于超参数 γ 对于设置先验而言并非无关紧要，因此我们使用 softmax 置信度（9）选择在测试时使用哪种模型。我们学习模型的集合，每个模型通过运行算法 1 来训练，其中算法 γ 的不同值为 γ =10^-i ，其中 i = 0、1、2、3、4、5、6 。图 1b（底部）显示了我们的方法在不同迭代次数 K 和 ERM（分别为蓝色和红色条形）之间的比较。为了区分整体学习的作用，我们学习了一组各自对应于不同初始化的基线模型。对于基线（ERM）和我们的方法，我们将集合中的模型数量固定为相同。将图 1b（底部）与图 1b（顶部）和图 1a（底部）进行比较，我们的集成方法可在不同的测试场景中实现更高的精度。我们观察到，随着迭代次数 K 的增加，我们的样本外性能会提高。同样在集成设置中，对于 USPS 数据集，我们看不到任何改进，我们推测这是在远离训练的域和靠近训练的域之间的良好性能之间进行权衡的产物。