codefroces这题有很深的trick，你能解开吗？大家好

大家好，欢迎阅读codeforces专题。
我们今天选择的问题是contest 1419的C题，目前有接近8000的人通过了本题。今天这题的难度不大，但是真的很考验思维，一不小心就会踩中陷阱，我个人觉得非常有意思，适合周末动动脑。
题目链接：
题意有一个叫做Killjoy的特工发明了一种新型的冠状病毒叫做Convid-2069 ，专门在codeforces平台上传播。这种病毒通过rating传播，只要两个人的rating一样并且其中一个感染了病毒，那么另外一个也会被感染。
这个病毒一开始的时候只有Killjoy自己感染了，他一共和n个人有联系。由于codeforces会定期举办比赛，参加比赛会改变一个人的rating ，由于codeforces的规则，导致所有参赛的人的rating变动的总量为0 ，也就是说有人升了一定会有人降，大家的总和保持不变。已知Killjoy自己不会参赛，请问最少需要多少次比赛可以将所有人都感染。
对于每一次比赛，可以不必所有人都参与，传染的发生不需要时间，瞬间就可以传染。很容易证明，我们一定可以在有限次比赛当中将所有人都感染。
样例首先输入一个t表示测试数据的组数(1 <=t <= 100) ，对于每一组数据第一行输入两个数，分别是n和x 。 n表示和Killjoy有接触的人的数量， x表示Killjoy自己的rating ， (2 <=n <=1000, -4000 <= x <= 4000) 。
第二行输入n个整数，表示这n个人的rating 。要求输出一个整数，表示最少需要的比赛数量(-4000 <= ai <= 4000) 。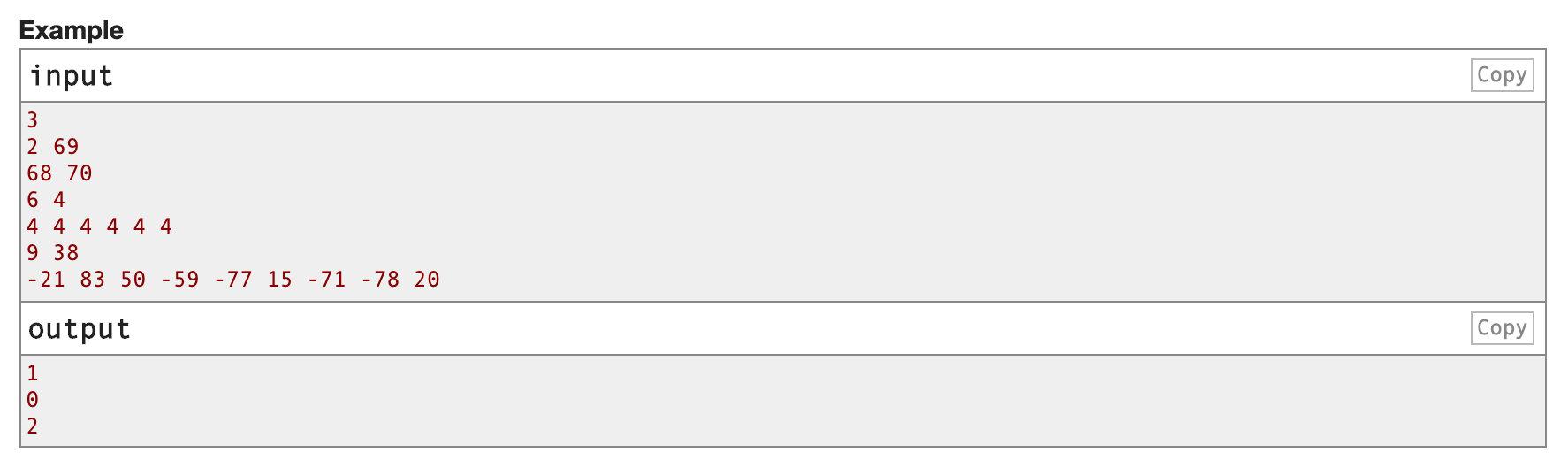
文章插图
题解这道题的思路非常直接，没什么弯弯绕，我们只需要观察一下样例就可以了。样例当中有三组数据刚好对应了三种情况。
我们先来看第一种情况：这n个人的rating都和x相等，那么意味着我们不需要比赛，就可以把所有人都感染了。结果当然是0 ，这一种非常简单，大家应该都可以想明白。
第二种情况也不难，第二种情况就是虽然大家的rating不全等于x ，但是大家的总和等于x * n 。也就是说rating大于x的减小到x ，小于x的增加到x ，刚好可以通过一次比赛让大家全部被感染，那么最终的答案就是1 。这对应样例当中的68 ，70的情况， x=69 ，很明显68的增加1 ， 70的减去1 ，就可以都变成69 。
前面两种理清楚了，再来看第三种情况，第三种情况也就是前面两种都不符合的情况。也就是我们通过一次比赛没办法让大家都等于x ，不过这并没有什么关系，因为题目当中并没有限制rating的范围。我们完全可以让其中n-1个人全部变成x ，由于要保证大家的rating变动之和等于0 ，所以让最后一个人来完成平衡的角色。
也就是说通过一次比赛，我们可以让n-1个人全部被感染，最后留下一个人。那么不难想出，我们只需要再多用一个回合就可以了。再多一个回合，我们可以让第n个人变成x ，让一个已经感染的人来完成平衡。那么，我们用了两个回合就完成了所有人的感染。
整理一下思路，其实这题分为三种情况，第一种情况是大家全部都等于x ，答案是0 。第二种情况是大家可以只需要一个回合就变成x ，如果上面两种情况都不满足的话，就额外再消耗一个回合即可。
这个思路也太简单了，很快我就写好了代码：
import math t = int(input()) for _ in range(t):n, x = list(map(int, input().split(' ')))arr = list(map(int, input().split(' ')))diff = 0sdiff = 0for i in range(n):diff += abs(arr[i] - x)sdiff += arr[i] - x# 如果所有人都等于x ，那么会在一开始就被感染完if diff == 0:print(0)# 如果可以通过一个回合让所有人的rating调整到x ，那么只需要一个回合elif sdiff == 0:print(1)else:print(2)但是很遗憾，当我提交了之后，并没有AC ，而是错在了第二组数据。我想了很久，才终于想到了其中的trick 。我先不说，大家先思考一下，看看能不能想到。
准备好了吗？
我们刚才列举的三种情况是没有问题的，但是我们遗漏了一种。就是这一开始的n个人当中，可能有人的rating就等于x ，所以他会在第一次比赛之前就感染。我们再想想最后一种情况，我们先把n-1个人的rating调整到x ，再把调整当中付出的代价交给其中一个人来承担。这也是我们需要第二个回合的原因，如果这n个人当中存在有人在开始之前就感染了，那么我们完全可以让这个已经感染的人来承担代价，这样我们就可以减少一个回合。
体现在代码当中，就是我们需要额外增加一个判断条件，判断一下这n个人当中是否存在有人的rating等于x ，会在一开始的时候就被感染。如果有的话，答案就是1 。