手推公式：LSTM单元梯度的详细的数学推导长短期记忆是复杂和先进的神

长短期记忆是复杂和先进的神经网络结构的重要组成部分。本文的主要思想是解释其背后的数学原理，所以阅读本文之前，建议首先对LSTM有一些了解。
介绍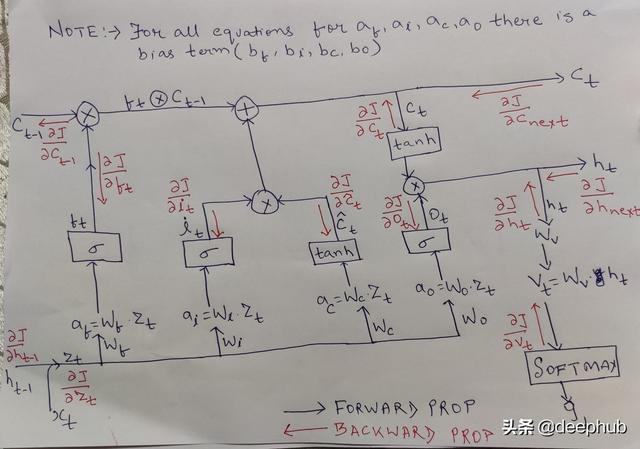
文章插图
上面是单个LSTM单元的图表。我知道它看起来可怕，但我们会通过一个接一个的文章,希望它会很清楚。
解释基本上一个LSTM单元有4个不同的组件。忘记门、输入门、输出门和单元状态。我们将首先简要讨论这些部分的使用，然后深入讨论数学部分。
忘记门
顾名思义，这部分负责决定在最后一步中扔掉或保留哪些信息。这是由第一个s型层完成的。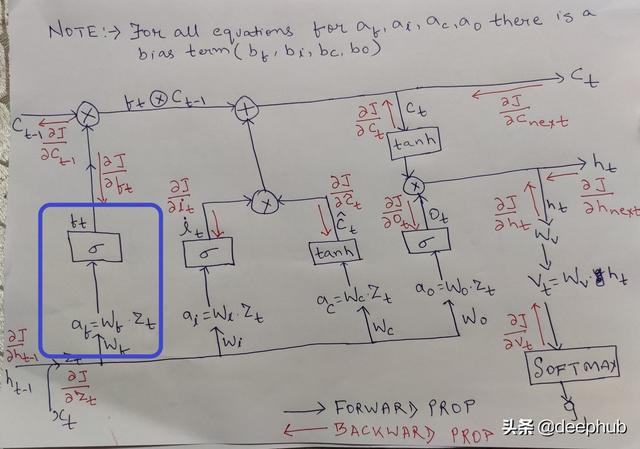
文章插图
根据ht-1(以前的隐藏状态)和xt(时间步长t的当前输入) ，它为单元格状态C_t-1中的每个值确定一个介于0到1之间的值。
文章插图
遗忘门和上一个状态
如果为1 ，所有的信息保持原样，如果为0 ，所有的信息都被丢弃，对于其他的值，它决定有多少来自前一个状态的信息被带入下一个状态。
输入门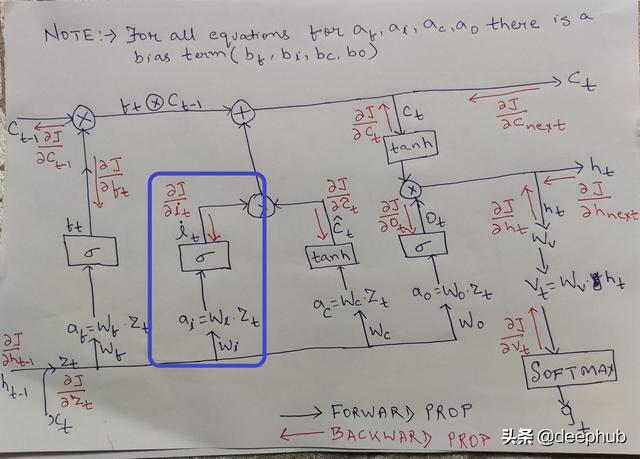
文章插图
Christopher Olah博客的解释在输入门发生了什么：
下一步是决定在单元格状态中存储什么新信息。这包括两部分。首先，一个称为"输入门层"的sigmoid层决定我们将更新哪些值。接下来，一个tanh层创建一个新的候选值的向量， C~t ，可以添加到状态中。在下一步中，我们将结合这两者来创建对状态的更新。
现在这两个值i 。 e i_t和c~t结合决定什么新的输入是被输入到状态。
单元状态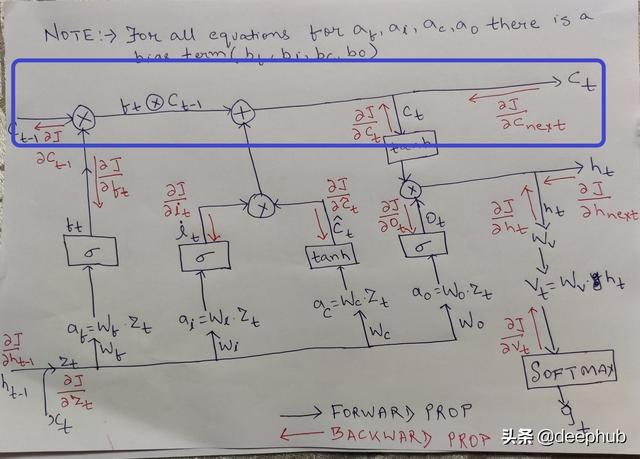
文章插图
【手推公式：LSTM单元梯度的详细的数学推导】单元状态充当LSTM的内存。这就是它们在处理较长的输入序列时比普通RNN表现得更好的地方。在每一个时间步长，前一个单元状态(Ct-1)与遗忘门结合，以决定什么信息要被传送，然后与输入门(it和c~t)结合，形成新的单元状态或单元的新存储器。
文章插图
状态的计算公式
输出门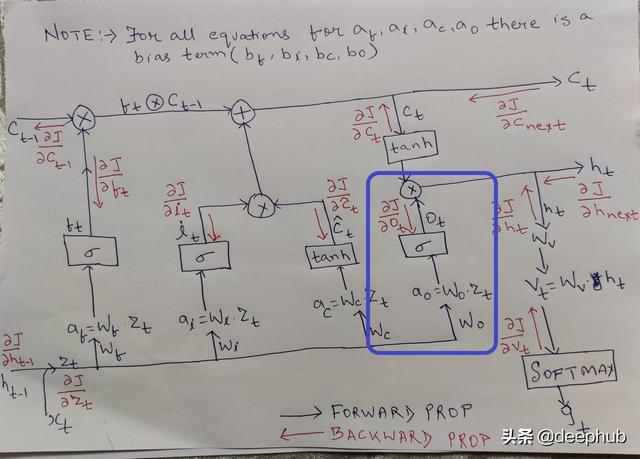
文章插图
最后， LSTM单元必须给出一些输出。从上面得到的单元状态通过一个叫做tanh的双曲函数，因此单元状态值在-1和1之间过滤。
LSTM单元的基本单元结构已经介绍完成，继续推导在实现中使用的方程。
推导先决条件推导方程的核心概念是基于反向传播、成本函数和损失。除此以外还假设您对高中微积分(计算导数和规则)有基本的了解。
变量:对于每个门，我们有一组权重和偏差，表示为:
· Wf,bf->遗忘门的权重和偏差
· Wi,bi->输入门的权重和偏差
· Wc,bc->单元状态的权重和偏差
· Wo,bo->输出门的权重和偏差
· Wv ,bv -> 与Softmax层相关的权重和偏差
· ft, it,ctiledet, o_t -> 输出使用的激活函数
· af, ai, ac, ao -> 激活函数的输入
J是成本函数，我们将根据它计算导数。注意(下划线(_)后面的字符是下标)
前向传播推导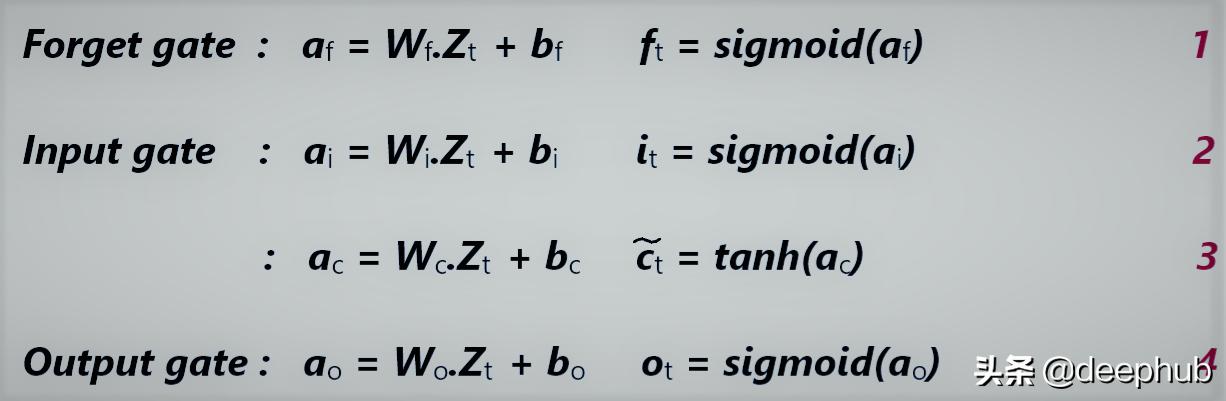
文章插图
门的计算公式
文章插图
状态的计算公式
以遗忘门为例说明导数的计算。我们需要遵循下图中红色箭头的路径。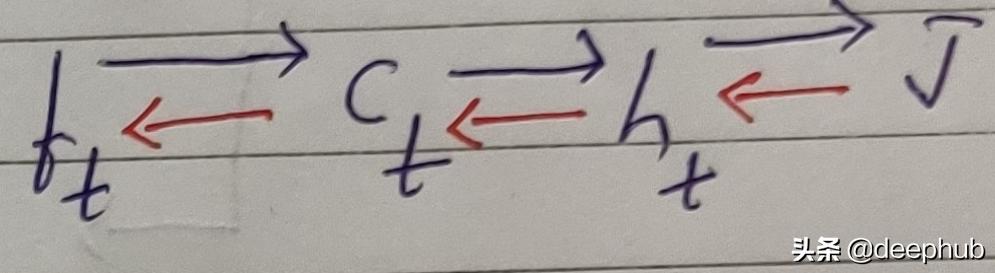
文章插图
我们画出一条从f_t到代价函数J的路径，也就是
ft→Ct→h_t→J 。
反向传播完全发生在相同的步骤中，但是是反向的
ft←Ct←h_t←J 。
J对ht求导， ht对Ct求导， Ct对f_t求导。
所以如果我们在这里观察， J和ht是单元格的最后一步，如果我们计算dJ/dht ，那么它可以用于像dJ/dC_t这样的计算，因为:
dJ/dCt = dJ/dht * dht/dCt(链式法则)
同样，对第一点提到的所有变量的导数也要计算。
现在我们已经准备好了变量并且清楚了前向传播的公式，现在是时候通过反向传播来推导导数了。我们将从输出方程开始因为我们看到在其他方程中也使用了同样的导数。这时就要用到链式法则了。我们现在开始吧。