强化学习的最基本概念马尔可夫决策过程简介( 二 ) 在本文中我将介绍强化学习的

从class3 中我们可以看到，该值是通过将立即回报（-2）与下两个状态的期望值相加来计算的。为了计算下一状态的期望值，我们可以将转移概率与状态的值相乘。因此，我们得到-2 +0.6* 10 +0.4*0.8等于4.3 。
马尔可夫奖励过程是一个具有奖励和价值的马尔可夫过程
马尔可夫决策过程到目前为止，我们已经了解了马尔可夫奖赏过程。但是，当前状态和下一个状态之间可能没有动作。马尔可夫决策过程（MDP）是具有决策的MRP 。现在，我们可以选择几个动作以在状态之间进行转换。
让我们在下图中查看MDP 。这里的主要区别在于，在采取行动后会立即获得奖励。在执行MRP时，状态变更后会立即获得奖励。这里的另一个区别是动作也可以导致学生进入不同的状态。根据学生的MDP ，如果学生采取Pub动作，则他可以进入class1 ， class2或class3 。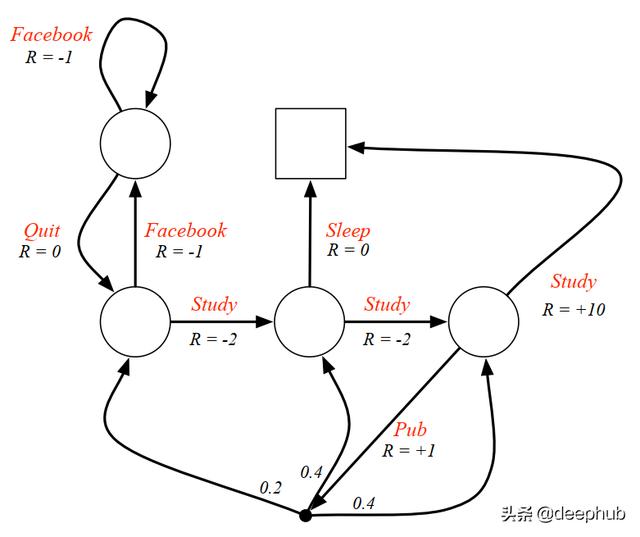
文章插图
给定这些动作，我们现在有了一个策略，该策略将状态映射到动作。它定义了代理人（在这种情况下是学生）的行为。策略是固定的（与时间无关），它们取决于操作和状态而不是时间步长。
基于策略，我们有一个状态值函数和一个动作值函数。状态值函数是从当前状态开始然后遵循策略的预期收益。另一方面，操作值函数是从当前状态开始，然后执行操作，然后遵循策略的预期收益。
通过使用Bellman方程，我们可以具有状态值函数（v）和动作值函数（q）的递归形式，如下所示。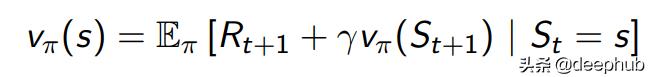
文章插图
状态值函数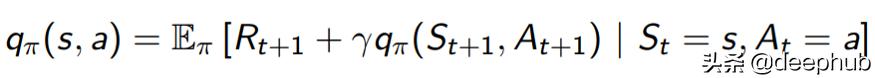
文章插图
动作值函数
为了使情况更清楚，我们可以在下图中再次查看带有gamma 0.1的 MDP 。假设在class3（红色圆圈）中，学生有50:50的政策。这意味着该学生有50％的机会Study或Pub 。我们可以通过将每个动作之后的每个预期收益相加来计算状态值。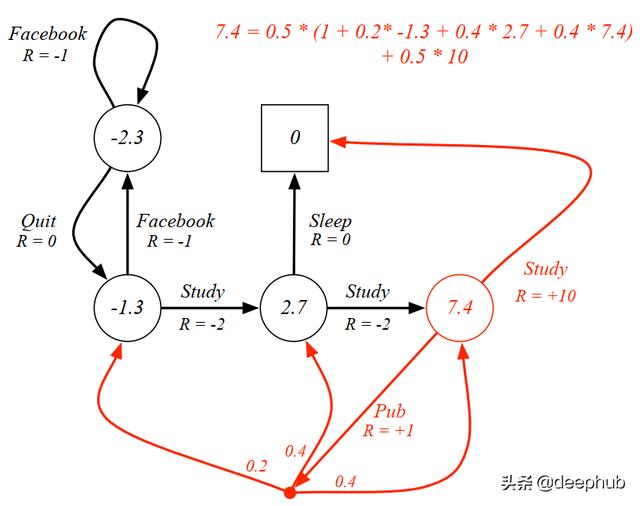
文章插图
通过将动作概率与下一个状态的期望值（0.5 * 10）相乘，可以计算出Study的期望值。相反， Pub操作具有多个导致不同状态的分支。因此，我们可以通过将动作概率（0.5）乘以动作值，从Pub中计算出期望值。可以通过将即时奖励与来自所有可能状态的期望值相加来计算操作值。可以通过1 + 0.2 * -1.3 + 0.4 * 2.7 + 0.4 * 7.4进行计算。
代理人的目标是最大化其价值。因此，我们必须找到导致最大值的最优值函数。在前面的示例中，我们通过对所有可能的操作的所有期望值求和来计算值。现在，我们只关心提供最大值的动作。在了解了最优值函数之后，我们有了最优策略并求解了MDP 。下图显示了针对每个状态的最优值和策略的MDP 。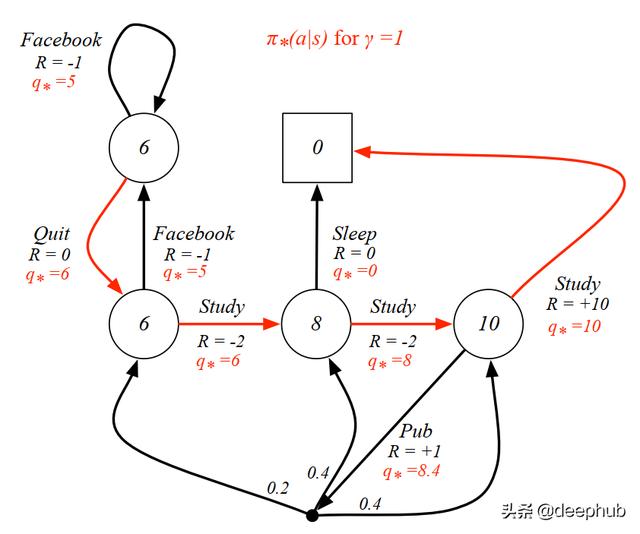
文章插图
具有最佳政策的学生MDP
结论总而言之，马尔可夫决策过程是具有动作的马尔可夫奖励过程，在此过程中，代理必须根据最佳价值和政策做出决策。
作者 Alif Ilham Madani
deephub翻译组