强化学习的最基本概念马尔可夫决策过程简介在本文中我将介绍强化学习的

文章插图
在本文中我将介绍强化学习的基本方面，即马尔可夫决策过程。我们将从马尔可夫过程开始，马尔可夫奖励过程，最后是马尔可夫决策过程。
目录马尔可夫过程
马尔可夫奖励过程
马尔可夫决策过程
马尔可夫过程马尔可夫决策过程(MDP)代表了一种强化学习的环境。我们假设环境是完全可见的。这意味着我们拥有了当前状态下做出决定所需的所有信息。然而，在我们讨论MDP是什么之前，我们需要知道马尔科夫性质的含义。
马尔可夫性质指出，未来是独立于过去的现在。它意味着当前状态从历史记录中捕获所有相关信息。例如，如果我现在口渴了，我想马上喝一杯。当我决定喝水的时候，这与我昨天或一周前口渴无关(过去的状态) 。现在是我做出决定的唯一关键时刻。
鉴于现在，未来独立于过去
除了马尔可夫性质外，我们还建立了一个状态转移矩阵，它存储了从每个当前状态到每个继承状态的所有概率。假设我在工作时有两种状态:工作(实际工作)和观看视频。当我工作时，我有70%的机会继续工作， 30%的机会看视频。然而，如果我在工作中看视频，我可能有90%的机会继续看视频， 10%的机会回到实际工作中。也就是说，状态转移矩阵定义了从所有状态(工作，观看视频)到所有继承状态(工作，观看视频)的转移概率。
了解了马尔可夫性质和状态转移矩阵之后，让我们继续讨论马尔可夫过程或马尔可夫链。马尔可夫过程是一个无记忆的随机过程，如具有马尔可夫性质的状态序列。
我们可以在下图中看到马尔科夫过程学生活动的一个例子。有几种状态，从class 1到最终状态Sleep 。每个圆中的数字表示转移概率。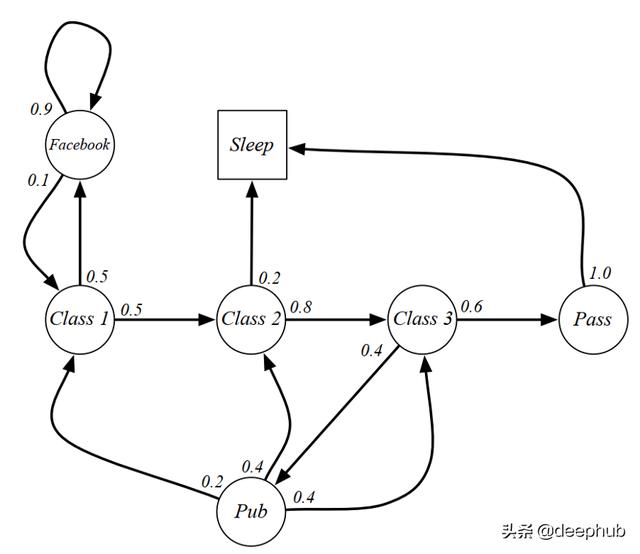
文章插图
我们可以从class 1到sleep这一过程中获取一些例子:
C1 C2 C3 Pass Sleep,C1 FB FB C1 C2 Sleep,C1 C2 C3 Pub C2 C3 Pass Sleep, and so on.
它们三个从相同的状态(class 1)开始，并以睡眠结束。然而，他们经历了不同的路径来达到最终状态。每一次经历都是我们所说的马尔科夫过程。
具有马尔可夫性质的随机状态序列是一个马尔可夫过程
马尔可夫奖励过程至此，我们终于理解了什么是马尔可夫过程。马尔可夫奖励过程(MRP)是一个有奖励的马尔可夫过程。这很简单，对吧?它由状态、状态转移概率矩阵加上奖励函数和一个折现因子组成。我们现在可以将之前的学生马尔科夫过程更改为学生MRP ，并添加奖励，如下图所示。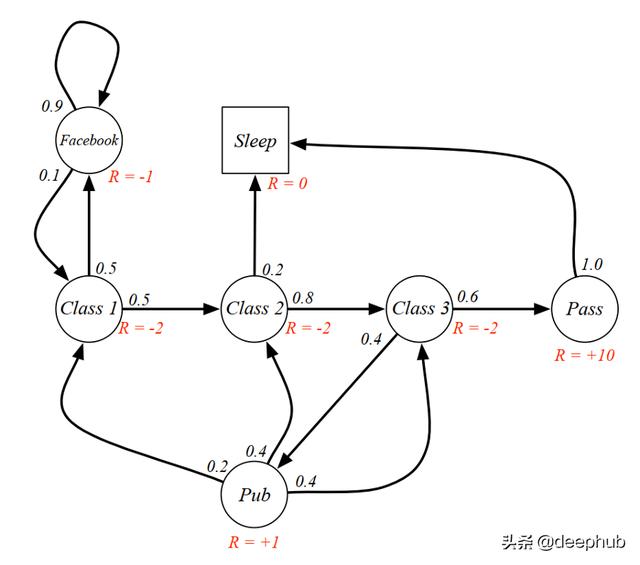
文章插图
【强化学习的最基本概念马尔可夫决策过程简介】要理解MRP ，我们必须了解收益和价值函数。
回报是从现在起的总折扣奖励。折扣因子是未来奖励的现值，其值在0到1之间。当折扣因子接近0时，它倾向于立即奖励而不是延迟奖励。当它接近1时，它将延迟奖励的价值高于立即奖励。
但是，您可能会问"为什么我们要增加折扣系数？" 。好吧，出于几个原因需要它。首先，我们希望通过将折扣系数设置为小于1来避免无限的回报。其次，立即获得的回报实际上可能更有价值。第三，人类行为表现出对立即获得奖励的偏好，例如选择现在购物而不是为将来储蓄。
收益（G）可以使用奖励（R）和折扣因子（γ）如下计算。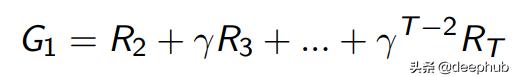
文章插图
从MRP中，我们可以得到一个从class 1开始的折现系数为0.5的示例收益。样本剧本是[C1 C2 C3 Pass] ，其收益等于-2 -2 * 0.5 -2 * 0.25 + 10 * 0.125 = -2.25 。
除了return之外，我们还有一个value函数，它是一个状态的预期收益。值函数确定状态的值，该值指示状态的可取性。使用Bellman方程，我们可以仅使用当前奖励和下一个状态值来计算当前状态值。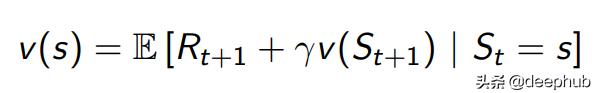
文章插图
这意味着我们只需要下一个状态即可计算一个状态的总值。换句话说，我们可以拥有一个递归函数，直到处理结束。
让我们再次看一下Gamma等于1的 MRP 。下图表示每个状态下都有一个值的MRP 。以前已经计算过该值，现在我们要用等式验证3类（红色圆圈）中的值。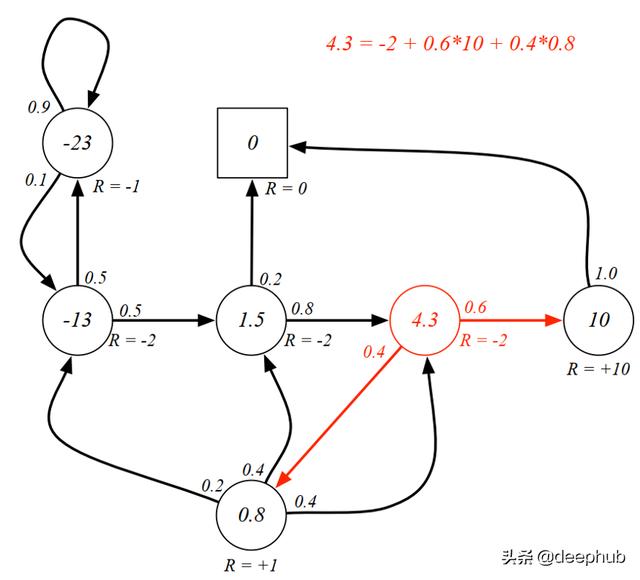
文章插图