最短路径|Dijkstra算法详细(单源最短路径算法)( 二 )
<6;i++) { len[i]=Integer.MAX_VALUE; } Queue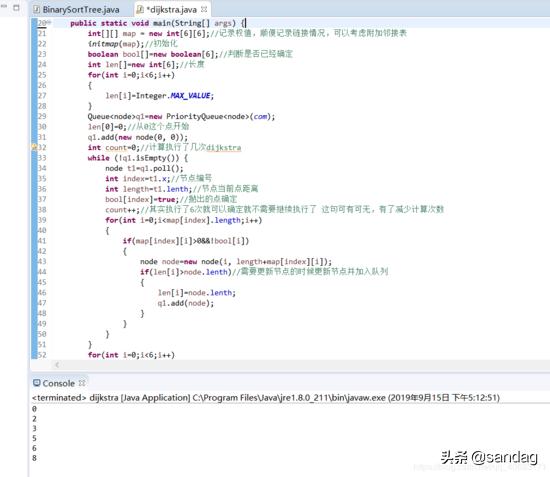 文章插图
文章插图
当然 , dijkstra算法比较灵活 , 实现方式也可能有点区别 , 但是思想是不变的:一个贪心思路 。 dijkstra执行一次就能够确定一个点 , 所以只需要执行点的总和次数即可完成整个算法 。
- 停产|华为mate40pro+疑似停产,为给P50系列留芯片,成最短命旗舰?
- 史上最短命旗舰!为了华为P50:Mate40部分机型疑似停产
- 用最短的时间,赚最高的工资
- leetcode之最短补全词
- 分子|科学家测量出有史以来最短时间间隔:仅为247仄秒
- 芯片|华为mate40pro+疑似停产,为给P50系列留芯片,成最短命旗舰?
- 设计|北大博士设计的无人驾驶船问世!可载人且自主规划路径和避障
- 「亲测」Thinkphp5 正则验证匹配出所有图片路径
- 齐鲁在线|发现设计师创“薪”的最IN路径,达内举办首期“大内高手”沙龙
- 路径|修改桌面保存路径图文教程,注册表改桌面目录从c盘修改到d盘方法
