像下山一样 ， 找到损失函数的最低点 。
文章插图
毫无疑问 ， 神经网络是目前使用的最流行的机器学习技术 。 所以我认为了解神经网络如何学习是一件非常有意义的事 。
为了能够理解神经网络是如何进行学习的 ， 让我们先看看下面的图片:
文章插图
如果我们把每一层的输入和输出值表示为向量 ， 把权重表示为矩阵 ， 把误差表示为向量 ， 那么我们就得到了上述的一个神经网络的视图 ， 它只是一系列向量函数的应用 。 也就是说 ， 函数将向量作为输入 ， 对它们进行一些转换 ， 然后把变换后的向量输出 。 在上图中 ， 每条线代表一个函数 ， 它可以是一个矩阵乘法加上一个误差向量 ， 也可以是一个激活函数 。 这些圆表示这些函数作用的向量 。
例如 ， 我们从输入向量开始 ， 然后将其输入到第一个函数中 ， 该函数用来计算其各分量的线性组合 ， 然后我们将获得的向量作为输出 。 然后把这个向量作为激活函数的输入 ， 如此类推 ， 直到我们到达序列中的最后一个函数 。 最后一个函数的输出就是神经网络的预测值 。
到目前为止 ， 我们已经讨论过神经网络是如何得到输出的 ， 这正是我们感兴趣的内容 。 我们知道神经网络只是将它的输入向量传递给一系列函数 。 但是这些函数要依赖于一些参数：权重和误差 。
神经网络如何通过学习得到这些参数来获得好的预测呢?
让我们回想一下神经网络实际上是什么：实际上它只是一个函数 ， 是由一个个小函数按顺序排列组成的大函数 。 这个函数有一组参数 ， 在一开始 ， 我们并不知道这些参数应该是什么 ， 我们仅仅是随机初始化它们 。 因此在一开始神经网络会给我们一些随机的值 。 那么我们如何改进他们呢？在尝试改进它们之前 ， 我们首先需要一种评估神经网络性能的方法 。 如果我们没有办法衡量模型的好坏 ， 那么我们应该如何改进模型的性能？
为此 ， 我们需要设计一个函数 ， 这个函数将神经网络的预测值和数据集中的真实标签作为输入 ， 将一个代表神经网络性能的数字作为输出 。 然后我们就可以将学习问题转化为求函数的最小值或最大值的优化问题 。 在机器学习领域 ， 这个函数通常是用来衡量我们的预测有多糟糕 ， 因此被称为损失函数 。 我们的问题就变成了找到使这个损失函数最小化的神经网络参数 。
随机梯度下降算法你可能很擅长从微积分中求函数的最小值 。 对于这种问题 ， 通常取函数的梯度 ， 令其等于0 ， 求出所有的解(也称为临界点) ， 然后从中选择使函数值最小的那一个 。 这就是全局最小值 。 我们能做同样的事情来最小化我们的损失函数吗？事实上是行不通的 ， 主要的问题是神经网络的损失函数并不像微积分课本中常见的那样简洁明了 。 它是一个极其复杂的函数 ， 有数千个、几十万个甚至数百万个参数 。 有时甚至不可能找到一个解决问题的收敛解 。 这个问题通常是通过迭代的方法来解决的 ， 这些方法并不试图找到一个直接的解 ， 而是从一个随机的解开始 ， 并在每次迭代中尝试改进一点 。 最终 ， 经过大量的迭代 ， 我们将得到一个相当好的解决方案 。
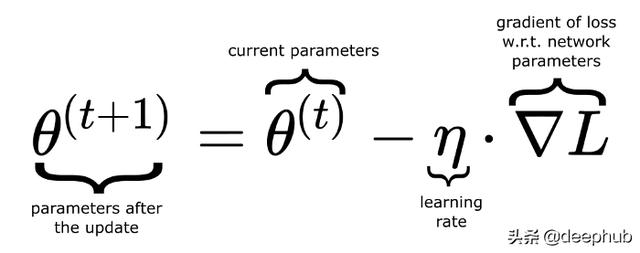
其中一种迭代方法是梯度下降法 。 你可能知道 ， 一个函数的梯度给出了最陡的上升方向 ， 如果我们取梯度的负值 ， 它会给我们最陡下降的方向 ， 也就是我们可以在这个方向上最快地达到最小值 。 因此 ， 在每一次迭代（也可以将其称作一次训练轮次）时 ， 我们计算损失函数的梯度 ， 并从旧参数中减去它（乘以一个称为学习率的因子）以得到神经网络的新参数 。
文章插图
其中θ（theta）表示包含神经网络所有参数的向量 。
在标准梯度下降法中 ， 梯度是将整个数据集考虑进来并进行计算的 。 通常这是不可取的 ， 因为该计算可能是昂贵的 。 在实践中 ， 数据集被随机分成多个块 ， 这些块被称为批 。 对每个批进行更新 。 这种方法就叫做随机梯度下降 。
上面的更新规则在每一步只考虑在当前位置计算的梯度 。 这样 ， 在损失函数曲面上运动的点的轨迹对任何变动都很敏感 。 有时我们可能想让这条轨迹更稳健 。 为此 ， 我们使用了一个受物理学启发的概念：动量 。 我们的想法是 ， 当我们进行更新时 ， 也考虑到以前的更新 ， 这会累积成一个变量Δθ 。 如果在同一个方向上进行更多的更新 ， 那么我们将"更快"地朝这个方向前进 ， 并且不会因为任何小的扰动而改变我们的轨迹 。 把它想象成速度 。

稿源：(未知)

【傻大方】网址：http://www.shadafang.com/c/111J2T612020.html

标题：神经网络如何学习的？