面试常考，项目易错！C/C++中的字节对齐( 四 ) 作者|李肖遥来源|技术让梦想更

cout <<"结构体m的大小:"<< sizeof(m) << endl; cout << endl; int offset_b = offsetof(struct m, a);// 获得成员a相对于m储存地址的偏移量 int offset_b1 = offsetof(struct m, b);// 获得成员a相对于m储存地址的偏移量 int offset_b2 = offsetof(struct m, c);// 获得成员a相对于m储存地址的偏移量 cout <<"a相对于m储存地址的偏移量:"<< offset_b << endl; cout << "b相对于m储存地址的偏移量:" << offset_b1 << endl; cout << "c相对于m储存地址的偏移量:" << offset_b2 << endl; //system("pause"); return 0;}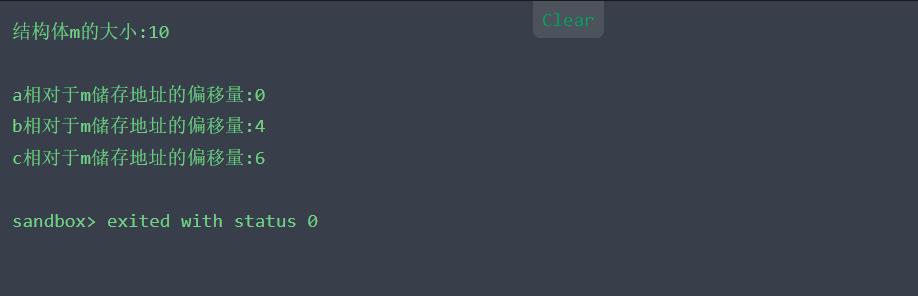
文章插图
对于这个结果，我们按刚才第一个例子我所分析的过程来分析这段代码，得到的是10；
故当我们将 #pragma pack 的n值小于所有数据成员长度的时候，结果将改变。
文章插图
对齐的作用和原因各个硬件平台对存储空间的处理上有很大的不同。如果不按照适合其平台要求对数据存放进行对齐，可能会在存取效率上带来损失。
比如有些平台每次读都是从偶地址开始，如果一个int型在32位地址存放在偶地址开始的地方，那么一个读周期就可以读出；
而如果存放在奇地址开始的地方，就可能会需要2个读周期，并对两次读出的结果的高低字节进行拼凑才能得到该int数据。那么在读取效率上下降很多，这也是空间和时间的博弈。
CPU每次从内存中取出数据或者指令时，并非想象中的一个一个字节取出拼接的，而是根据自己的字长，也就是CPU一次能够处理的数据长度取出内存块。总之， CPU会以它“最舒服的”数据长度来读取内存数据
举个例子如果有一个4字节长度的指令准备被读取进CPU处理，就会有两种情况出现：

4个字节起始地址刚好就在CPU读取的地址处，这种情况下， CPU可以一次就把这个指令读出，并执行，内存情况如下

文章插图

而当4个字节按照如下图所示分布时

文章插图
假设CPU还在同一个地址取数据，则取到第一个4字节单元得到了1、2字节的数据，但是这个数据不符合需要的数啊，所以CPU就要在后续的内存中继续取值，这才取到后面的4字节单元得到3、4字节数据，从而和前面取到的1、2字节拼接成一个完整数据。
而本次操作进行了两次内存读取，考虑到CPU做大量的数据运算和操作，如果遇到这种情况很多的话，将会严重影响CPU的处理速度。
因此，系统需要进行内存对齐，而这项任务就交给编译器进行相应的地址分配和优化，编译器会根据提供参数或者目标环境进行相应的内存对齐。

文章插图
什么时候需要进行内存对齐一般情况下都不需要对编译器进行的内存对齐规则进行修改，因为这样会降低程序的性能，除非在以下两种情况下：

这个结构需要直接被写入文件
这个结构需通过网络传给其他程序

文章插图
对齐的实现可以通知给编译器传递预编译指令，从而改变对指定数据的对齐方法。
unsigned int calc_align(unsigned int n,unsigned align) { if ( n / align * align == n) return n; return (n / align + 1) * align; } 不过这种算法的效率很低，下面介绍一种高效率的数据对齐算法：
unsigned int calc_align(unsigned int n,unsigned align) { return ((n + align - 1)} 这种算法的原理是：
(align-1) ：对齐所需的对齐位，如：2字节对齐为1 ， 4字节为11 ， 8字节为111 ， 16字节为1111...
(&~(align-1)) ：将对齐位数据置位为0 ，其位为1
(n+(align-1)) & ~(align-1) ：对齐后的数据

文章插图
总结通常，我们写程序的时候，不需要考虑对齐问题，编译器会替我们选择目标平台的对齐策略。
但正因为我们没注意这个问题，导致编辑器对数据存放做了对齐，而我们如果不了解的话，就会对一些问题感到迷惑。