线性方程组的解集及其几何意义( 二 ) 我们解决现实问题时可以自由

这个列空间，我们应该不陌生了，上一章中很多时候都是把矩阵看成列向量的排列，考虑 A x = b 的解的情况时其实就是在列向量中进行分析的。列空间在分析矩阵中各列向量的线性相关性时很有帮助：只有各列线性无关时，这 n 个列才能张成 n 维空间，这时就说这个矩阵的秩为 n ；而假如这里面有 1 列和其他某列线性相关，那么这 n 个列就只能张成 n ? 1 维空间，这个矩阵的秩就是 n ? 1 ；也就是说，矩阵的秩说明了这个矩阵的列向量最多能张成多少维。
如下图中，A = [ a 1 a 2 a 3 ]，由于有两个向量线性相关，导致 3 个列向量只能张成 2 维，因此 A 的秩为 2 。所以 A x 得不到任意三维向量 b，也就是 A x = b 并不对所有 b 成立（只有 b 是 A 列空间中的向量时才成立）。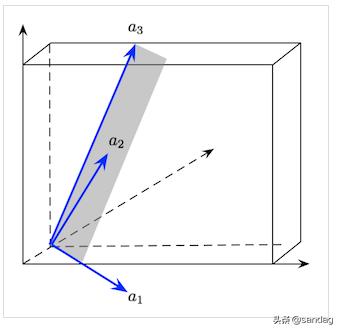
文章插图
更进一步，非齐次线性方程组 A x = b 中，如果 A 已知，x 和 b 未知，此时我们关注的问题是 A 的列向量能张成多少维；如果 A 和 b 已知，我们关注的问题就是 A 中 n 个列向量如何线性表示能表示成 b，这时候我们如果提前知道 A 的列空间达不到 b 的维数，那么这些列向量就一定无法线性组合出 b。
四、零空间齐次方程 A x = 0 的全部解组成的集合，称为矩阵 A 的零空间，记作 Nul A。
当 A 中的列向量线性无关时，A x = 0 只有零解，这时 A 的零空间就是 0 ；而只要 A 中的列向量线性相关，A x = 0 就存在非零解，这时 A 的零空间就是一个维度大于 0 的空间。
关于列空间和零空间的讨论先在这里打住，之后会进一步讨论它们之间的关系和各自的意义。目前只要知道列空间是由 A 的列向量张成的，而零空间的意义更隐晦一些，是 A x = 0 的所有解组成的空间。从列空间能看出 A 各列的线性相关关系，列向量越相关，列空间维度越低。从零空间也能看出 A 各列的线性相关性，列向量越相关，零空间维度越高。而负责量化描述 A 列向量有多么线性相关的，是一个叫做秩的东西。
# 参考资料：

线性代数及其应用：第3版/（美）莱（Lay, D.C.）著；沈复兴等译. ——北京：人民邮电出版社， 2007.7
麻省理工学院的线性代数公开课