线性方程组的解集及其几何意义我们解决现实问题时可以自由

我们解决现实问题时可以自由选取其中任意一个作为模型。我个人认为，线性方程组是最“质朴”的形式；向量方程则是与几何建立了关系，这将方便我们进行更直观的推理；矩阵方程则是向量方程的一种“封装” ，是向量方程的一种抽象，它将具体的向量形式隐藏，提供给我们一个简洁的 API 形式——矩阵。未来将要介绍的很多概念就是基于对这一层封装的研究，如果到时候我们发现某个概念理解有困难，不妨转换思路到向量方程或线性方程组的形式进行分析。
此外，我们之前还进行了关于线性方程组解集的讨论，在这章我们对其进一步探讨。
一、齐次线性方程组形如 A x = 0 的线性方程组称为齐次方程组。显然，x = 0 是方程的解，这个解太平凡了，以致于就叫平凡解。我们平常更关心的是它还有没有别的解，即非平凡解。下面以一个例子分析一下：
例：判断下列齐次方程组是否有非平凡解，表示其解集。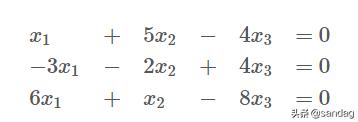
文章插图
对于这类求解集的问题，我们可以直接对增广矩阵化简，得到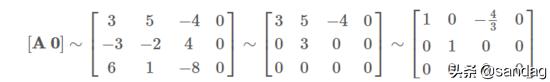
文章插图
从最后的行最简形式，我们可以得到解：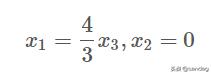
文章插图
，其中 x 3 是自由变量。所以 x 的通解就是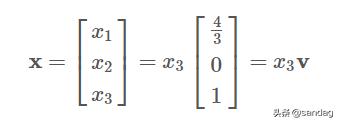
文章插图
。也就是说，A x = 0 的解是三维空间（因为向量 v 是三维的）中的一条直线（因为只有一个自由变量）。进一步推广，我们不难想象，如果解集中有 p 个自由变量，则解集就是 m 维空间（ m 为 A 的行数）中，p 个向量张成的空间。如果没有自由变量（也就是 A 各列线性无关），那么就有 0 个向量张成的空间，即 Span { 0 }，A x = 0 也就只有平凡解。
二、非齐次线性方程组非齐次线性方程组形如 A x = b，为了方便对比，我们把上面那个例子改为一个非齐次方程组进行分析：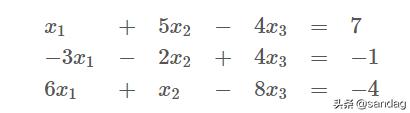
文章插图
老套路，我们对这个方程组的增广矩阵行化简：
文章插图
化简后可以得到方程组的解为：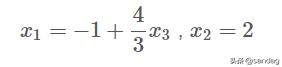
文章插图
，其中 x 3 是自由变量。我们把这个解集用向量的形式表示出来就是：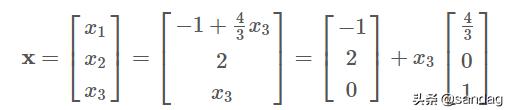
文章插图
注意到这个向量可分解为一个常数向量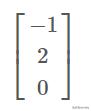
文章插图
和一个可任意伸缩的向量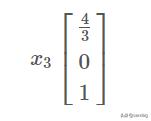
文章插图
，而且，常数向量就是行化简后矩阵的最后一列，而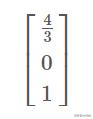
文章插图
同样是齐次方程组的解。这是因为非齐次方程组只是最后一列由 0 换成了 b，而且最后一列不会影响前面三列，所以齐次和非齐次方程组行化简后，变量的对应系数是相同的（系数矩阵就是前三列），非齐次方程组的解仅仅只比齐次方程组的解多了一个常数向量。例如齐次方程组的解集为 x = t v，则非齐次方程组的解集就是 x = p + t v，其中 t 为任意实数。从几何的角度来看，就是齐次方程组的解集经向量 p 平移得到非齐次方程组的解集。这个 p 的学名就叫做特解。
注意，这里讲齐次方程组和非齐次方程组的解有一个前提，就是非齐次方程组首先要是有解的，如果 0 变成 b 导致方程组没有解，那么也就不能用齐次方程组的解集平移了。
【线性方程组的解集及其几何意义】结合之前总结的齐次线性方程组解的性质，当方程组含有 p 个自由变量时，齐次方程组的解集是 p 个向量的张成空间，而非齐次方程组解集只是这个空间进行了平移（前提是非齐次方程组有解），并没有改变这个空间的基本性质（比如空间的维度）。
三、列空间矩阵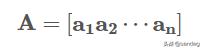
文章插图
的各个列向量线性组合组成的集合，就是 A 的列空间。记作 Col A，即
Col A = Span { a 1 , a 2 , ? , a n }