编译器|解析卷积的高速计算中的细节，一步步代码带你飞( 二 ) 作者：ManasSahni编译：ronghuaiy

那么维度本身的顺序呢？通常对于四维张量，比如CNNs ，你会听到NCHW, NHWC等存储顺序。我将在这篇文章中假设NCHW——如果我有N块HxW图像的C通道，那么所有具有相同N个通道的图像都是重叠的，在该块中，同一通道C的所有像素都是重叠的，以此类推。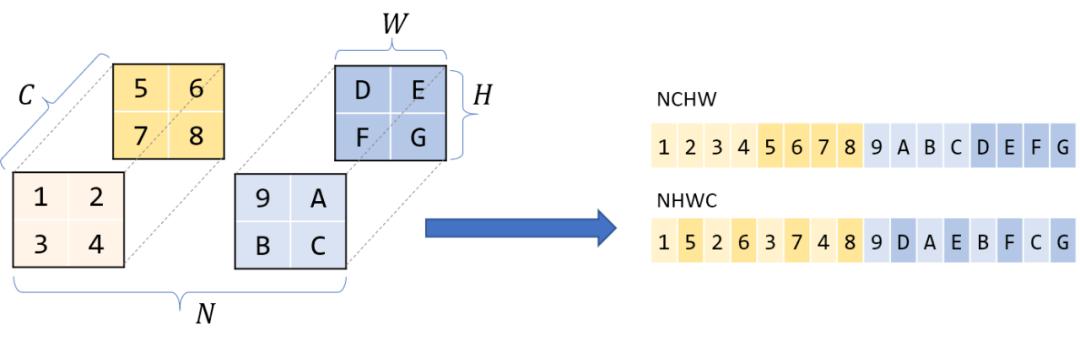
文章插图
Halide
这里讨论的许多优化都需要在底层使用神秘的C语法，甚至是程序集进行干预。这不仅使代码难以阅读，还使尝试不同的优化变得困难，因为我们必须重新编写整个代码。 Halide是c++中的一种嵌入式语言，它帮助抽象这些概念，并被设计用来帮助编写快速图像处理代码。通过分解算法(要计算什么)和计划(如何/何时计算) ，可以更容易地试验不同的优化。我们可以保持算法不变，并使用不同的策略。
我将使用Halide来表示这些较低级别的概念，但是你应该能够理解足够直观的函数名，以便理解。
从卷积到GEMM
我们上面讨论的简单卷积已经很慢了，一个更实际的实现只会因为步长、膨胀、填充等参数而变得更加复杂。我们可以继续使用基本的卷积作为一个工作示例，但是，正如你看到的，从计算机中提取最大性能需要许多技巧—在多个层次上进行仔细的微调并充分利用现有计算机体系结构的非常具体的知识。换句话说，如果我们希望解决所有的复杂性，这将是一项艰巨的任务。
我们能不能把它转化成一个更容易解决的问题？也许矩阵乘法？
矩阵乘法，或matmul ，或Generalized Matrix Multiplication (GEMM)是深度学习的核心。它用于全连接层、RNNs等，也可用于实现卷积。
毕竟，卷积是带有输入padding的滤波器的点积。如果我们把滤波器放到一个二维矩阵中，把输入的小patch放到另一个矩阵中，然后把这两个矩阵相乘，就会得到相同的点积。与CNNs不同，矩阵乘法在过去几十年里得到了大量的研究和优化，在许多科学领域都是一个关键问题。
上面将图像块放到一个矩阵中的操作称为im2col，用于图像到列。我们将图像重新排列成矩阵的列，使每一列对应一个应用卷积滤波器的patch 。
考虑这个普通的，直接的3x3卷积：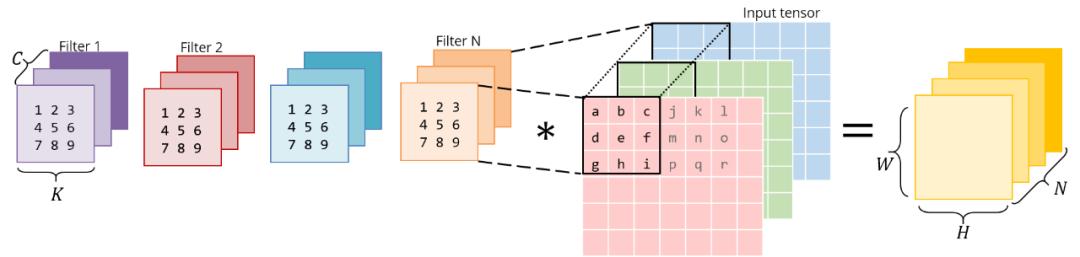
文章插图
下面是与矩阵乘法相同的操作。正确的矩阵是im2col的结果——它必须通过复制原始图像中的像素来构造。左边的矩阵有conv权值，它们已经以这种方式存储在内存中。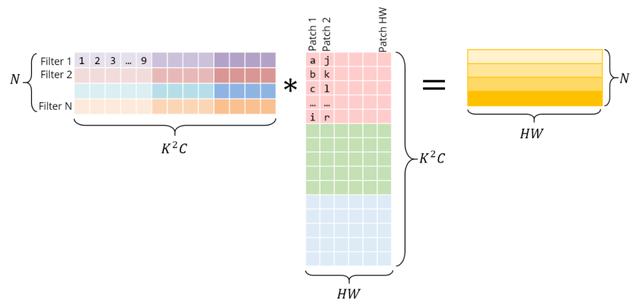
文章插图
注意，矩阵乘积直接给出了conv输出——不需要额外的“转换”到原始形式。
为了清晰起见，我将每个patch都单独显示在这里。然而，在现实中，不同的图像块之间往往存在一定的重叠，因此im2col会产生一定的内存重复。生成这个im2col缓冲区和膨胀的内存所花费的时间，必须通过GEMM实现的加速来抵消。
利用im2col ，我们已经将卷积运算转化为矩阵乘法。我们现在可以插入更多通用的和流行的线性代数库，如OpenBLAS、Eigen等，利用几十年的优化和仔细的调优，有效地计算这个matmul 。
如果我们要证明im2col转换所带来的额外工作和内存是合理的，那么我们需要一些非常严重的加速，所以让我们看看这些库是如何实现这一点的。这也很好地介绍了在系统级进行优化时的一些通用方法。
虽然以前有过不同形式的convolution-as-GEMM思想，但Caffe是第一个在CPU和GPU上对通用convs使用这种方法的深度学习库之一，并显示了较大的加速。这里：:a-memo一个非常有趣的阅读来自于Yanqing Jia本人(Caffe的创始人)关于这个决定的起源，以及关于“临时”解决方案的想法。
加速GEMM
原始的方法
在这篇文章的其余部分，我将假设GEMM被执行为
和之前一样，首先让我们对基本的，课本上的矩阵乘法进行计时：
for i in 0..M: for j in 0..N: for k in 0..K: C[i, j] += A[i, k] * B[k, j]使用Halide:
Halide::Buffer C, A, B; Halide::Var x, y;C(x,y) += A(k, x) *= B(y, k); // loop bounds, dims, etc. are taken care of automatically最里面的一行执行2个浮点运算(乘法和加法) ，并执行M?N?K次，因此这个GEMM的FLOPs是2MNK 。
我们来测量一下它在不同矩阵大小下的性能：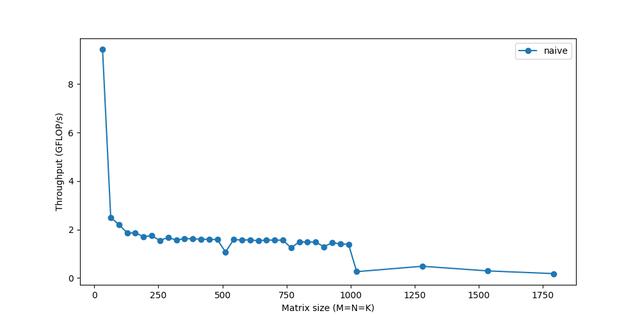
文章插图
我们的性能才刚刚达到顶峰的10% ！虽然我们将研究使计算更快的方法，但一个反复出现的主题是，如果我们不能快速获得数据，仅仅快速计算数据是不够的。由于内存对于较大的矩阵来说是一个越来越大的问题，因此性能会逐渐下降。你最后看到的急剧下降，表示当矩阵变得太大而无法放入缓存时，吞吐量突然下降—你可以看到系统阻塞。