详解微软 ALUM：当语言模型遇到对抗训练作者|山竹小果来源|NewBeeNLP（

文章插图
文章插图
作者 | 山竹小果
来源 | NewBeeNLP（id：NewBeeNLP）
今天分享来自微软最近关于语言模型和对抗训练的工作：

论文：Adversarial Training for Large Neural LangUage Models
源码：

文章插图
TL;DR本文把对抗训练用到了预训练和微调两个阶段，对抗训练的方法是针对embedding space ，通过最大化对抗损失、最小化模型损失的方式进行对抗，在下游任务上取得了一致的效果提升。
有趣的是，这种对抗训练方法不仅能够在BERT上有提高，而且在RoBERTa这种已经预训练好的模型上也能有所提高，说明对抗训练的确可以帮助模型纠正易错点。

方法：ALUM（大型神经语言模型的对抗性训练）
实现：在embedding space添加扰动，最大化对抗损失
应用：任何基于Transformer的语言模型的预训练或微调

文章插图
预备知识BPE编码为了解决词汇表外单词的问题，使用Byte-Pair Encoding（BPE）（Sennrich et al. ， 2015）或其变体（Kudo and Richardson ， 2018）将标记划分为子词单元，生成固定大小的子词词汇，以便在训练文本语料库中紧凑地表示单词。
BPE词表既存在char-level级别的字符，也存在word-level级别的单词。通过BPE得到了更加合适的词表，这个词表可能会出现一些不是单词的组合，但是这个本身是有意义的一种形式。
流程：

1.确定subword词表大小
2.统计每一个连续字节对的出现频率，并保存为code_file 。这个是git中learn-bpe完成
3.将单词拆分为字符序列并在末尾添加后缀“ ” ，而后按照code_file合并新的subword ，首先合并频率出现最高的字节对。例如单词birthday ，分割为['b', 'i', 'r', 't', 'h', 'd', 'a', 'y'] ，查code_file ，发现'th'出现的最多，那么合并为['b', 'i', 'r', 'th', 'd', 'a', 'y'] ，最后，字符序列合并为['birth', 'day'] 。然后去除'',变为['birth', 'day'] ，将这两个词添加到词表。这个是apply-bpe完成。
4.重复第3步直到达到第2步设定的subword词表大小或下一个最高频的字节对出现频率为1

文章插图
模型：ALUM基于几个关键想法：

扰动embedding空间，优于直接对输入文本应用扰动。
通过虚拟对抗训练为标准目标添加正则化项。

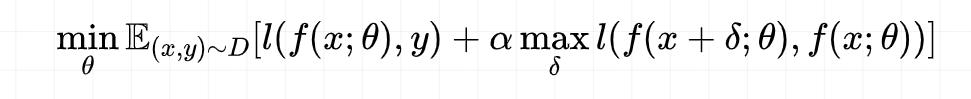文章插图
其中预训练阶段α = 10 ，微调阶段 α = 1 。
因为有最大化操作，所以训练昂贵。有利于embedding邻域的标签平滑。
文中观点：虚拟对抗训练优于传统对抗训练，特别是当标签可能有噪声时。
例如， BERT pretraining使用masked words作为自监督的标签，但在许多情况下，它们可以被其他词取代，形成完全合法的文本。但BERT中，给到被替换的word的标签均为负。
算法首先使用标准目标（1）训练模型；然后使用虚拟对抗训练（3）继续训练。

文章插图
第4-6行为求最大梯度步骤，以找到使对抗性损失最大化的扰动（反局部平滑性）。 K越大的近似值越高，但成本更高。为了在速度和性能之间取得良好的平衡，本文实验K=1.
泛化与鲁棒性文中表示，通过使用ALUM进行对抗性的预训练，能够提高广泛的NLP任务的泛化和鲁棒性（如后述实验结论所示）。之前的研究较多发现，对抗训练会损害泛化能力。
先前关于泛化和鲁棒性之间冲突的工作通常集中在有监督的学习环境中。调和两者的一些初显成果也利用了未标记的数据，例如自训练（Raghunathan等人， 2020年）。
此外，假设通过扰动embedding空间而不是输入空间， NLP中的对抗训练可能无意中偏向于流形扰动而不是规则扰动。
什么是流形流形学习的观点：认为我们所观察到的数据实际上是由一个低维流形映射到高维空间的。由于数据内部特征的限制，一些高维中的数据会产生维度上的冗余，实际上这些数据只要比较低的维度的维度就能唯一的表示。
所以直观上来讲，一个流形好比是一个d维的空间，在一个m维的空间中（m>d）被扭曲之后的结果。需要注意的是流形不是一个形状，而是一个空间。举个例子，比如说一块布，可以把它看成一个二维的平面，这是一个二维的空间，现在我们把它扭一扭(三维空间),它就变成了一个流形，当然不扭的时候，它也是一个流形，欧氏空间是流形的一种特殊情况。