np-hDeepMind与谷歌又出大招！用神经网络解决NP-hard的MIP问题动力|米文

文章插图
编译 | 陈彩娴
近日，DeepMind 与 Google Research 团队共同发布了一项工作，用神经网络与机器学习方法来解决混合整数规划（MIP）问题！

文章插图

论文地址：https://arxiv.org/pdf/2012.13349.pdf
在解决现实中遇到的大规模混合整数规划（Mixed Integer Programming, MIP）实例时，MIP 求解器要借助一系列复杂的、经过数十年研究而开发的启发式算法，而机器学习可以使用数据中实例之间的共享结构，从数据中自动构建更好的启发式算法。
在这篇工作中，他们将机器学习应用于 MIP求解器的两个关键子任务，生成了一个高质量的联合变量赋值（joint variable assignment），并缩小了该变量赋值与最优赋值之间的目标值差距。他们构建了两个对应的、基于神经网络的组件，即 Neural Diving 与 Neural Branching，使其可用于基本的 MIP 求解器上，比如 SCIP。
其中，Neural Diving 学习一个深度神经网络，为其整数变量生成多个部分赋值，并用 SCIP 来解决由此产生的未赋值变量的较小 MIP，以得到高质量的联合赋值。而 Neural Branching 学习一个深度神经网络，在分支定界中进行变量选择决策，以用一棵小树来缩小目标值的差距。这是通过模仿他们所提出的 Full Strong Branching（全强分支）的新变量来实现。
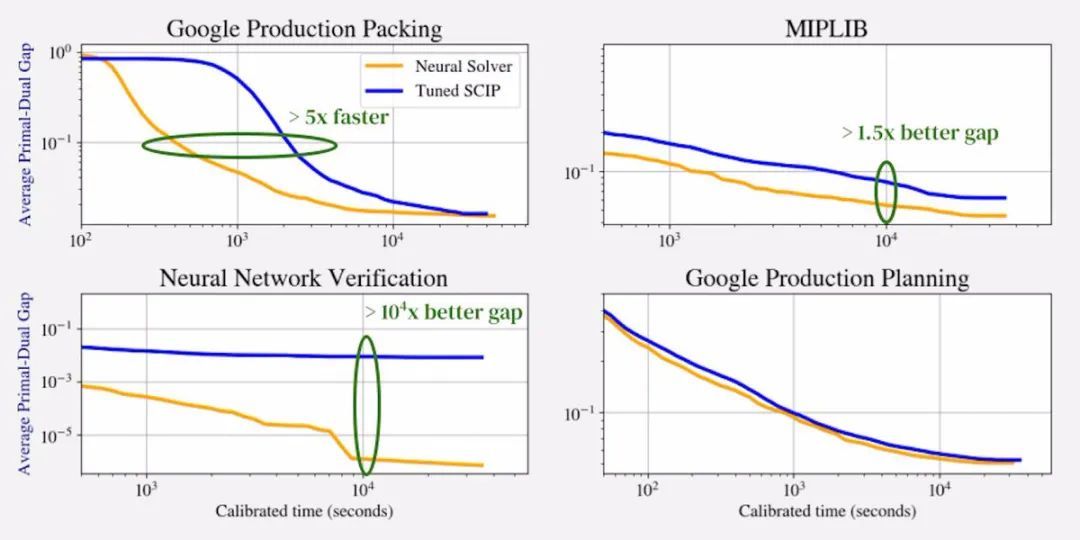
作者团队将神经网络在多个真实世界的数据集（包括两个谷歌生产数据集和 MIPLIB）上分别进行了训练，以进行评估。在所有数据集中，大多数实例在预求解后都有 10^3 至 10^6 个变量和约束，明显大于以前的学习方法。
对比求解器与大时间限制下原问题与对偶问题在一组留出（hold-out）实例上的差距平均值，学习增强的 SCIP 在3个具有最大 MIP 的数据集（一共有5个数据集）上实现了 1.5x、2x 和 104x 的更好差距，在第4个数据集上以5x的速度更快实现 10% 的差距，并在第5个数据集上取得了与 SCIP 不相上下的表现。
该团队介绍，据了解，他们的方法是第一个在大规模现实世界应用数据集和 MIPLIB 上都展示了比 SCIP 有更大进步的学习方法。

【 np-hDeepMind与谷歌又出大招！用神经网络解决NP-hard的MIP问题】概念简介
1.1 分支定界
常见的解决 MIP 过程是递归地构建搜索树，在每个节点处分配部分整数，并使用每个节点所收集的信息最终收敛于最佳（或接近最佳）分配。在每一步，我们都必须选择一个叶子节点，从中“分支”。在这个节点上，我们可以解决线性规划（LP）松弛问题，将在该节点上的固定变量的范围限制为它们的指定值。这为我们提供了该节点中所有子节点的真实目标值的有效下限。
如果这个界限大于已知的可行分配，那么我们就可以安全地修剪搜索树的这一部分，因为该节点的子树中不存在原问题的最优解。如果我们决定扩展这个节点，那么我们必须从该节点的一组未固定变量中选择一个变量作为分支。一旦选择了一个变量，我们就采取分支步骤，将两个子节点添加到当前节点。一个节点有选定变量的域，该域会被约束为大于或等于其父节点处的 LP 松弛值的上限。另一个节点将所选变量的域约束为小于或等于其 LP 松弛值的下限。树被更新，过程再次开始。
这个算法被称为“分支定界”（branch-and-bound）算法。线性规划是这个过程的主要工作，既可以在每个节点上导出对偶边界，又可以为一些更复杂的分支启发式算法确定分支变量。理论上，搜索树的大小可以随着问题的输入大小呈指数增长，但在许多情况下，搜索树可能很小，并且是一个提出节点选择和变量选择启发式算法来使树尽可能保持小的活跃研究领域。
1.2 原始启发式
原始启发式是一种尝试找到可行但不一定最佳的变量赋值的方法。任何此类可行的赋值都提供了 MIP 最佳值的保证上限。在 MIP 求解期间的任何点找到的任何此类边界都被称为“原始边界”。
原始启发式可以独立于分支定界运行，但它们也可以在分支定界树中运行，并尝试从搜索树中的给定节点找到不固定变量的可行赋值。生成较低原始边界的、更好的原始启发式方法允许在分支定界过程中修剪更多的树。简单的四舍五入就是原始启发式的一个例子。另一个例子是潜水（diving），试图通过深度优先的方式从给定节点中探索搜索树来找到可行的解决方案。