智能车电感差比和差加权算法研究( 四 ) ▲李佳昊王谢援吴涛在研究基于电感的智

其次，尝试对水平电感差比和偏置算法进行了建模，公式如下
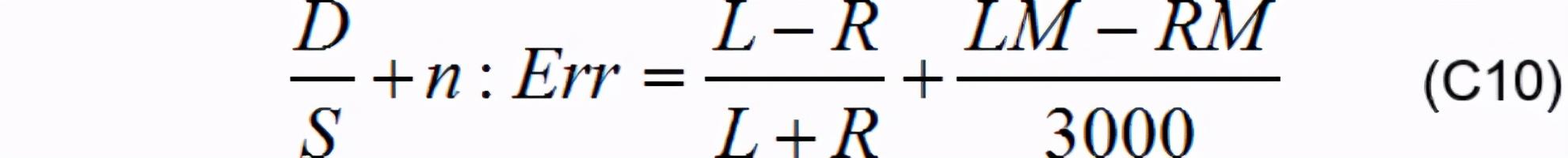文章插图
将中间两纵向电感的差值乘以1/3000才得到一条不错的曲线。
文章插图
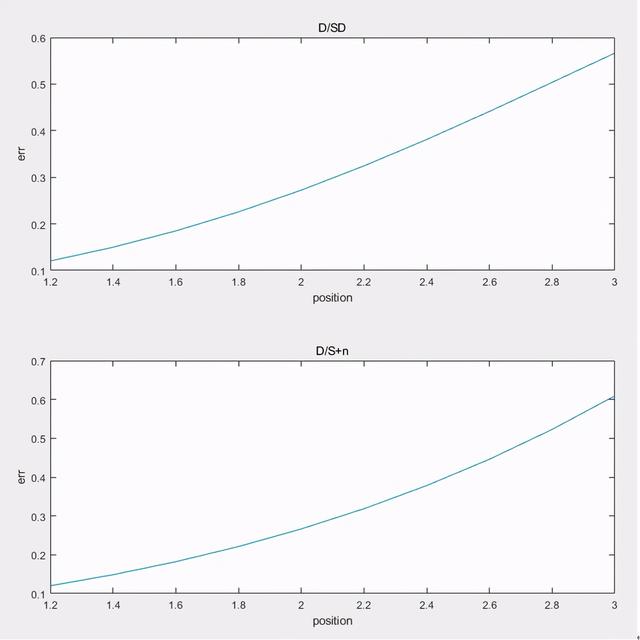
▲ 图C2.4 曲线对比
图C2.4中，差比和偏置算法的内环区数据斜率要小于差比和差加权算法，而曲率又更大，小车更难切内环行驶。如果想让小车切内环行驶，就需要增加中间两纵电感的权值，但是如果算法的曲线出现了差比和加权算法的内环区反增的趋势，则会产生过调抖动，容易冲出赛道；若是出现了曲率过大的情况，那么小车就更难切内环行驶。
差比和所输出误差值曲线更加贴合一次曲线，能够支持小车入弯切内环行驶，而其他很多算法无法做到这一点，这也是差比和差算法出色的优势之一。
2.5 小结本章从不同角度入手，用各种方式证明了电感差比和差算法对弯道道型有着良好的亲和度，同时也具有很高的稳定性；证明了电感差比和差加权算法相较于电感差比和加权算法，水平电感差比和偏置算法的优势。
除此之外，电感差比和差算法由于分母的减小，其输出误差所需的比例系数也有所下降，小车在长直道型上行驶时的抖动也会有所下降。需要注意的是电感差比和差相较于电感差比和加权算法，赛道适应性有所下降，需要对各项参数投入更多关注。
直接调节电感差比和差加权算法，可能会因无法直观的了解各参数而走弯路，故建议先调出一套相对稳定的电感差比和加权方案，然后将其改写为电感差比和差加权算法。这样做的理论依据有二，其一，长直道上，纵向电感值接近于零，两算法差距不会太大。第二，由第二章所建立的模型中可以看出，小车沿中线行驶时，两加权算法的输出误差曲线相似，差比和差加权算法的参数可由差比和加权算法参数微调获得。
3.2修复过调以电感差比和加权算法调试出一套慢速稳定的方案后，将算式改写为差比和差加权算法，此时由于分子的下降，小车在弯道道型出现小幅度过调。此时轻微降低比例系数（约为差比和加权算法的0.7到0.8倍）即可完全拟合。
文章插图
[1]殷剑宏，吴开亚.图论及其算法[M].中国科学技术大学出版社,2003.
[2]卓晴,黄开胜,邵贝贝.学做智能车：挑战"飞思卡尔"杯[M].北京:北京航空航天大学出版社,2007.
[3]王盼宝主编.智能车制作[M].北京:清华大学出版社,2017.
[4]谭浩强著.C程序设计[M].北京:清华大学出版社,2003.
[5]张文春.汽车理论[M].北京:机械工业出版社.2005.