智能车电感差比和差加权算法研究 ▲李佳昊王谢援吴涛在研究基于电感的智

文章插图
▲ 李佳昊王谢援吴涛
在研究基于电感的智能车方向控制时发现了弯道拟合度高的差比和差加权算法。本文从算法的发现、算法原理出发对差比和差算法进行描述，并使用MATLAB、Python建模对其弯道拟合度高的特点与其他优势进行证明。
关键词：智能车；电感；MATLAB；
文章插图
在研究基于电感的智能车方向控制时，首先使用了较为普遍的电感差比和加权引导方案。调试过程中，发现小车对于弯道的敏感度不理想，故多次尝试修改横纵电感权重，或将代码推翻重写，寻求理想的结果。
进行数次代码推翻重写后，偶然产生了一次期望之外的结果，小车绕赛道逆时针行驶（在调方案）时，其对于弯道的敏感性和拟合程度都在预期之上，成功进行速度测试后，开始精调参数。针对小车对弯道敏感度超出预期的现象，初步采取了降低方向比例控制系数（P）的措施，调整后，发现小车在一些顺时针方向弯道上的行驶出现较大问题，针对问题进行排查、分析、数学论证后，产生了电感方向控制的差比和差加权算法。本文从问题的发现与解决出发，详细描述电感方向控制的差比和差加权算法的发现、原理、参数调试方法，并使用MATLAB建立模型解释其工作原理。
文章插图
1.1 算法的发现过程电感差比和差加权算法是在进行电感差比和加权算法调试时发现的。在调试过程中，建立电感差比和算法公式：
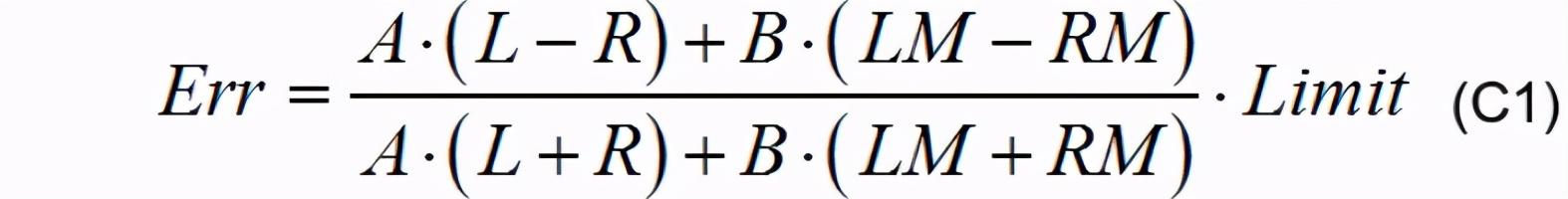文章插图
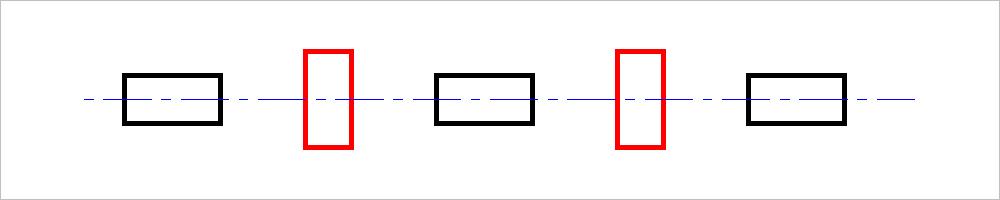
公式C1中， LM、RM是左中、右中两个电感获取电流经硬件、软件放大后的输出值， L、R是左、右两个电感的输出值， LIMIT是一个限幅系数， A、B是加权参数，电感的排布方式参考图C1.1 ，由左到右分别是L,LM,M,RM,R 。
文章插图
▲ 图C1.1 电感排布图
将公式C1的输出误差输入智能车方向控制系统，发现小车对于弯道的拟合效果差，多次调节B参数、方向控制比例系数，弯道拟合效果有所上升，但仍然不理想。在当时初步判定是参数调节的思路错误，以及遍历程度有所不足，故多次重新进行数学推演、参数遍历，尝试获得更优的结果。
一次算法推倒后的参数遍历中偶然产生了逆时针行驶时弯道的敏感性、拟合程度高于预期的现象。为增强弯道拟合效果，适当的降低了比例系数，但调整后产生了顺时针行驶困难、S型弯道难以拟合、大半径弯道切外环行驶等问题。对问题进行排查，发现在复制、粘贴时偶然将算法公式写成：
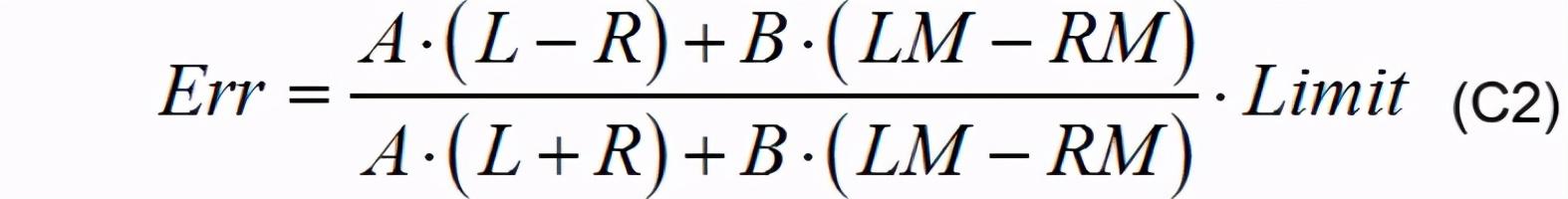文章插图
公式C2的左右不对称性造成了小车于逆时针（LM>RM）赛道的适应性良好，却对顺时针赛道适应性差的现象。对于排查后产生的问题，没有立刻进行修复处理，而是先对其逆时针赛道的良好适应性进行了分析。
首先尝试对错误算法逆时针赛道良好适应性的产生进行理论假设，当小车入弯时，电感差比和加权算法中位于分子上加权的(LM+RM)增大，导致err产生减小趋势，该减小趋势导致电感差比和对于弯道的敏感度下降。而当把分母上的(LM+RM)改为(LM-RM)后，小车入弯时err的分母增大趋势显然下降， err产生的减小趋势更弱。因此，小车对逆时针赛道的适应性增强了。