使用Python进行异常检测( 三 ) 异常检测可以作为异常值分析的一项统计

首先，定义一个函数来计算真正例、假正例和假反例：
def tpfpfn(ep):tp, fp, fn = 0, 0, 0for i in range(len(y)):if p[i] <= ep and y[i][0] == 1:tp += 1elif p[i] <= ep and y[i][0] == 0:fp += 1elif p[i] > ep and y[i][0] == 1:fn += 1return tp, fp, fn列出低于或等于平均概率的概率。
eps = [i for i in p if i <= p.mean()]检查一下列表的长度
len(eps)输出：
133根据前面讨论的公式定义一个计算f1分数的函数：
def f1(ep):tp, fp, fn = tpfpfn(ep)prec = tp/(tp + fp)rec = tp/(tp + fn)f1 = 2*prec*rec/(prec + rec)return f1所有函数都准备好了！
现在计算所有epsilon或我们之前选择的概率值范围的f1分数。
f = []for i in eps:f.append(f1(i))f输出：
[0.14285714285714285, 0.14035087719298248, 0.1927710843373494, 0.1568627450980392, 0.208955223880597, 0.41379310344827586, 0.15517241379310345, 0.28571428571428575, 0.19444444444444445, 0.5217391304347826, 0.19718309859154928, 0.19753086419753085, 0.29268292682926833, 0.14545454545454545,这是f分数表的一部分。长度应该是133 。
f分数通常在0到1之间，其中f1得分越高越好。所以，我们需要从刚才计算的f分数列表中取f的最高分数。
现在，使用“argmax”函数来确定f分数值最大值的索引。
np.array(f).argmax()输出：
131现在用这个索引来得到阈值概率。
e = eps[131]e输出：
6.107184445968581e-05找出异常实例我们有临界概率。我们可以从中找出我们训练数据的标签。
如果概率值小于或等于该阈值，则数据为异常数据，否则为正常数据。我们将正常数据和异常数据分别表示为0和1 ，
label = []for i in range(len(df)):if p[i] <= e:label.append(1)else:label.append(0)label输出：
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0,这是标签列表的一部分。
我将在上面的训练数据集中添加此计算标签：
df['label'] = np.array(label)df.head()
文章插图
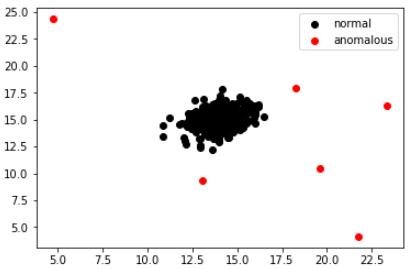
我在标签为1的地方用红色绘制数据，在标签为0的地方用黑色绘制。以下是结果。
文章插图
有道理吗？
是的，对吧？红色的数据明显异常。
结论【使用Python进行异常检测】我试图一步一步地解释开发异常检测算法的过程，我希望这是可以理解的。如果你仅仅通过阅读就无法理解，建议你运行每一段代码。那就很清楚了。