使用Python进行异常检测( 二 ) 异常检测可以作为异常值分析的一项统计

首先，导入必要的包
import pandas as pd import numpy as np导入数据集。这是一个excel数据集。在这里，训练数据和交叉验证数据存储在单独的表中。所以，让我们把训练数据带来。
df = pd.read_excel('ex8data1.xlsx', sheet_name='X', header=None)df.head()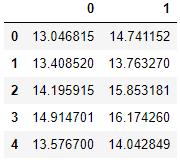
文章插图
让我们将第0列与第1列进行比较。
plt.figure()plt.scatter(df[0], df[1])plt.show()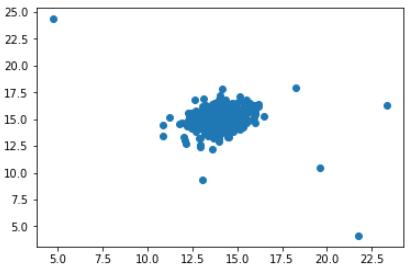
文章插图
你可能通过看这张图知道哪些数据是异常的。
检查此数据集中有多少个训练示例：
m = len(df)计算每个特征的平均值。这里我们只有两个特征：0和1 。
s = np.sum(df, axis=0)mu = s/mmu输出：
014.112226114.997711dtype: float64根据上面“公式和过程”部分中描述的公式，让我们计算方差：
vr = np.sum((df - mu)**2, axis=0)variance = vr/mvariance输出：
01.83263111.709745dtype: float64现在把它做成对角线形状。正如我在概率公式后面的“公式和过程”一节中所解释的，求和符号实际上是方差
var_dia = np.diag(variance)var_dia输出：
array([[1.83263141, 0.],[0., 1.70974533]])计算概率：
k = len(mu)X = df - mup = 1/((2*np.pi)**(k/2)*(np.linalg.det(var_dia)**0.5))* np.exp(-0.5* np.sum(X @ np.linalg.pinv(var_dia) * X,axis=1))p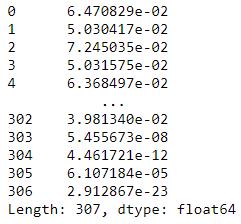
文章插图
训练部分已经完成。
下一步是找出阈值概率。如果概率低于阈值概率，则示例数据为异常数据。但我们需要为我们的特殊情况找出那个阈值。
对于这一步，我们使用交叉验证数据和标签。
对于你的案例，你只需保留一部分原始数据以进行交叉验证。
现在导入交叉验证数据和标签：
cvx = pd.read_excel('ex8data1.xlsx', sheet_name='Xval', header=None)cvx.head()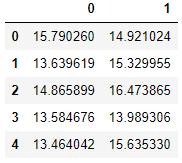
文章插图
标签如下：
cvy = pd.read_excel('ex8data1.xlsx', sheet_name='y', header=None)cvy.head()
文章插图
我将把'cvy'转换成NumPy数组，因为我喜欢使用数组。不过，数据帧也不错。
y = np.array(cvy)输出：
# 数组的一部分array([[0],[0],[0],[0],[0],[0],[0],[0],[0],这里， y值0表示这是一个正常的例子， y值1表示这是一个异常的例子。
现在，如何选择一个阈值？
我不想只检查概率表中的所有概率。这可能是不必要的。让我们再检查一下概率值。
p.describe()输出：
count3.070000e+02mean5.905331e-02std2.324461e-02min1.181209e-2325%4.361075e-0250%6.510144e-0275%7.849532e-02max8.986095e-02dtype: float64如图所示，我们没有太多异常数据。所以，如果我们从75%的值开始，这应该是好的。但为了安全起见，我会从平均值开始。
因此，我们将从平均值和更低的概率范围。我们将检查这个范围内每个概率的f1分数。