二叉树:公共祖先问题
本来是打算将二叉树和二叉搜索树的公共祖先问题一起讲 , 后来发现篇幅过长了 , 只能先说一说二叉树的公共祖先问题 。
236. 二叉树的最近公共祖先链接:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q , 最近公共祖先表示为一个结点 x , 满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先) 。 ”
例如 , 给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
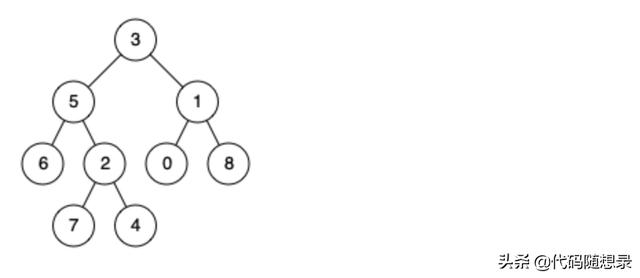 文章插图
文章插图
【二叉树:公共祖先问题】236. 二叉树的最近公共祖先
示例 1:输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1输出: 3解释: 节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4输出: 5解释: 节点 5 和节点 4 的最近公共祖先是节点 5 。 因为根据定义最近公共祖先节点可以为节点本身 。
说明:
- 所有节点的值都是唯一的 。
- p、q 为不同节点且均存在于给定的二叉树中 。
那么二叉树如何可以自底向上查找呢?
回溯啊 , 二叉树回溯的过程就是从低到上 。
后序遍历就是天然的回溯过程 , 最先处理的一定是叶子节点 。
接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢 。
「如果找到一个节点 , 发现左子树出现结点p , 右子树出现节点q , 或者 左子树出现结点q , 右子树出现节点p , 那么该节点就是节点p和q的最近公共祖先 。 」
使用后序遍历 , 回溯的过程 , 就是从低向上遍历节点 , 一旦发现如何这个条件的节点 , 就是最近公共节点了 。
递归三部曲:
- 确定递归函数返回值以及参数
但我们还要返回最近公共节点 , 可以利用上题目中返回值是TreeNode *, 那么如果遇到p或者q , 就把q或者p返回 , 返回值不为空 , 就说明找到了q或者p 。
代码如下:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) - 确定终止条件
代码如下:
if (root == q || root == p || root == NULL) return root;- 确定单层递归逻辑
我们在二叉树:递归函数究竟什么时候需要返回值 , 什么时候不要返回值? 中说了 递归函数有返回值就是要遍历某一条边 , 但有返回值也要看如何处理返回值!
如果递归函数有返回值 , 如何区分要搜索一条边 , 还是搜索整个树呢?
搜索一条边的写法:
if (递归函数(root->left)) return ;if (递归函数(root->right)) return ;搜索整个树写法:left = 递归函数(root->left);right = 递归函数(root->right);left与right的逻辑处理;看出区别了没?「在递归函数有返回值的情况下:如果要搜索一条边 , 递归函数返回值不为空的时候 , 立刻返回 , 如果搜索整个树 , 直接用一个变量left、right接住返回值 , 这个left、right后序还有逻辑处理的需要 , 也就是后序遍历中处理中间节点的逻辑(也是回溯)」 。
那么为什么要遍历整颗树呢?直观上来看 , 找到最近公共祖先 , 直接一路返回就可以了 。
- 聚焦突发公共事件科技传播 2020中国科技传播论坛举行
- 二叉树的存储
- 化石|人类真的没有天敌?一动物差点吃光人类祖先,至今仍有人感到害怕
- 玛雅人|高智商玛雅人,祖先或来自中国,其文化中带有大量“中国元素”
- 科学家|科学家:人类的祖先或许做了件“丑事”,才导致人类容易患上疾病
- 老虎|人类真的没有天敌?有一种动物差点吃光人类祖先,至今有人仍害怕
- |什么动物既没有祖先,也没有子孙?哈哈哈神评居然能做到全国统一
- 鳄鱼|那些可怕的巨型动物:鳄鱼就像公共汽车一样大,会吞噬蛇的巨大青蛙
- 金字塔|古埃及人开始修金字塔的时,我们的祖先在干啥?说出来你可能不信
- 南方古猿|人类当真没有天敌?一动物差点吃光人类祖先,至今有人依然害怕
