水稻|欧拉对“级数”的研究，发现了其他数学家几十年未能发现的结论考古学家|长江|袁隆平

文章图片

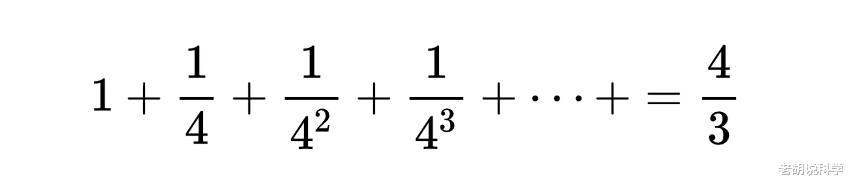
文章图片

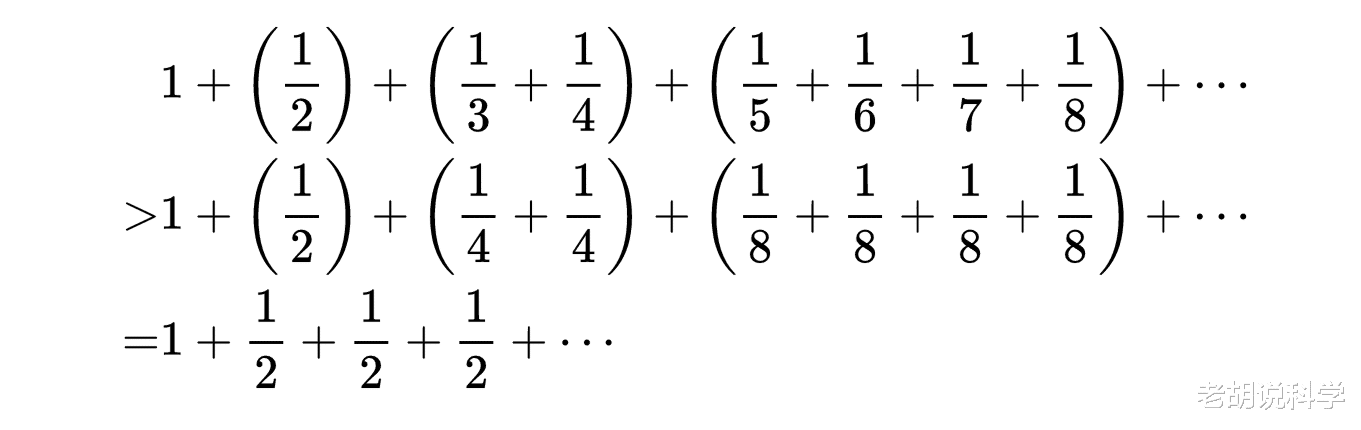
文章图片

文章图片

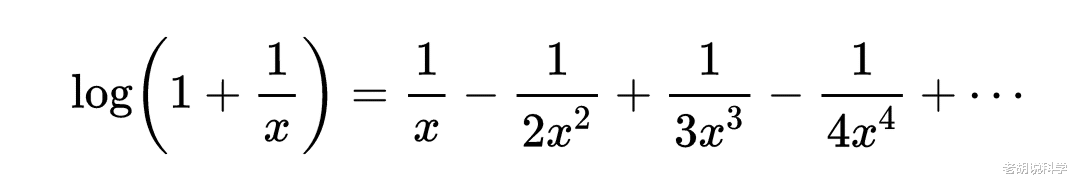
文章图片

文章图片

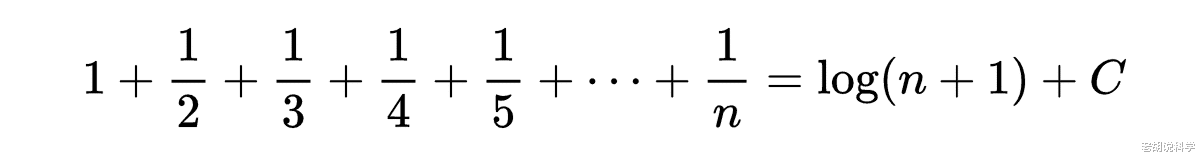
文章图片

文章图片

文章图片

文章图片

文章图片

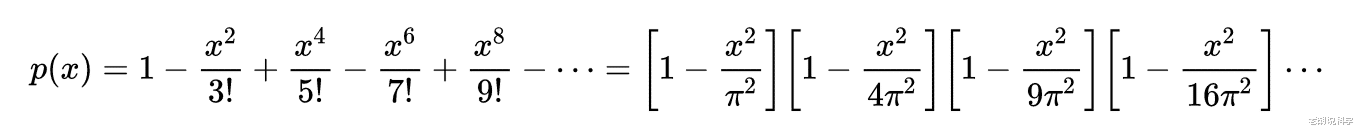
文章图片

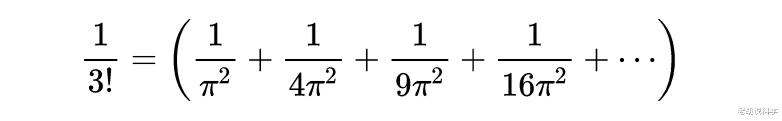
文章图片

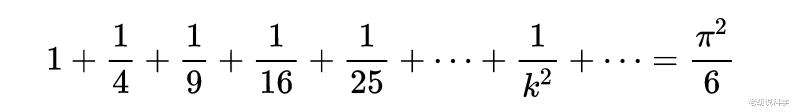
数学史上级数出现得很早，在两千多年前人们就有了粗糙的级数思想。古希腊时期，亚里士多德就知道公比小于1（大于零）的几何级数可以求出和数。芝诺的二分法涉及到把1分解成无穷级：
阿基米德在《抛物线图形求积法》一书中，使用几何级数去求抛物线弓形面积，并且得出了级数：
中国古代《庄子·天下》中的“一尺之捶，日取其半，万世不竭”含有极限的思想，用数学形式表达出来也是无穷级数。
到了中世纪，由于数学家和哲学家对一些涉及到无穷思想的悖论展开了激烈的争论，使得关于无穷级数的研究开展起来。最具代表的是法国数学家奥雷姆用最初等的方法证明了调和级数：
是发散的，用现在的形式可表示为：
中世纪的级数理论，从本质上看没有突破性进展，它的主要贡献并不在于所得到的具体结果，而是在于促使人们接受一种新的观点，即在数学中可以自由的承认无限过程。这对后来理解无穷过程做了铺垫，为形式化处理级数奠定了思想基础。
早期数学家仅凭直觉就认为级数是可以收敛的，并将级数从有限项自然地拓展为无限项使用，这导致了有限法则无限拓展的产生。 17世纪，伴随着微积分的产生，许多数学家通过微积分的基本运算与级数运算的形式化结合，得到了一些初等函数的幂级数展开式，并且级数在解析运算中被普遍用来代表函数而成为微积分的有力工具，这就使得无穷级数成为微积分不可缺少的部分。
1669年，牛顿在他的《用无限多项方程的分析学》中，用级数反演法给出了sinx ， cosx的幂级数， arcsinx ， arctanx和e^x的级数展开。格雷戈里得到了tanx ， secx等函数的级数，莱布尼茨也在1673年独立地得到了sinx ， cosx和arctanx等函数的无穷级数展开式，以及圆面积和双曲线面积的具体展开式。在微积分的早期研究中，有些函数如指数函数等超越函数的处理相当困难，然而人们发现，若用它们的级数来处理，则非常有成效。因此，无穷级数从一开始就是莱布尼茨、牛顿等人微积分工作的一个重要部分。有时使用无穷级数是为了计算一些特殊的量，如π和e以及求隐函数的显式解。
17世纪后期和18世纪，为了适应航海、天文学和地理学的发展，摆在数学家们面前的问题之一是函数表的插值。由于对函数表的精确度要求较高，数学家们开始寻求较好的插值方法，牛顿和格雷戈里给出了著名的内插公式：