爱因斯坦■三角形内角和一定是 180°吗？绝世传奇，怪诞的非欧几何相对论

文章图片

文章图片

文章图片

文章图片

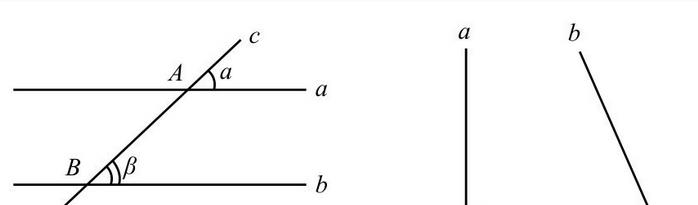
文章图片

文章图片

文章图片
自从数学诞生之日起，什么是它最伟大或者说最引人注目的发明呢？可能的答案有两个：一个是微积分，另一个是非欧几何。其中非欧几何对我们的触动也许更大。因为它太不平常了，它的发现有如哥伦布发现新大陆、弗洛伊德发现无意识，在人类的视野中打开了一片广阔的新天地，一片无人走过的、肥沃的处女地，人类在这里可以尽情地耕耘、收获。
千年以来，欧几里得几何一直被认为是唯一的几何学，《几何原本》中的内容也被当成不可更改的至高真理，而欧几里得在《几何原本》中提出的五个公设也当然地被视为这至高真理的核心。这五个公设分别是：
1、给定两点，可连接一线段。
2、线段可无限延长。
3、给定中心和圆上一点，可作一个圆。
4、所有直角彼此相等。
5、如一直线与两直线相交，且在同侧所交的两个内角之和小于两个直角，则这两直线无限延长后必定在该侧相交。
第五条公理又称平行公理（ParallelPostulate），简单来说就是：过直线外一点有且只有唯一一条直线与已知直线平行，这是欧氏几何的理论基础。被欧几里得认为是理所当然、无需证明的，是他整个几何学的基础理论。那么实际情形是不是真的这样呢？前面四个公设大家都没有什么意见，它们都简单明了、一目了然、令人信服。这第五公设就不大一样了，它要长得多，作为一个应该是不言而喻的公设显然不够自明。
因此，便有许多数学家试图通过各种方法，例如通过前面四条公设以及欧几里得的五条公理，来证明之。但结果无一成功。于是便有聪明人反其道而行之，否定它，看会有什么结果。这一否定便掀开了几何学乃至整个数学史上革命性的一页一非欧几何的诞生。
最早创立非欧几何的是高斯，但他并未公布之，这我们上面刚刚说过了，所以这个创立者的荣誉就归于罗巴切夫斯基了。
罗巴切夫斯基1793年生于俄罗斯的下诺夫哥罗德，在他只有7岁时父亲就去世了，母亲被迫搬到了比下诺夫哥罗德更加偏远的喀山。罗巴切夫斯基从小刻苦学习，成绩优异，从小学到大学都得到了奖学金，免费上学， 1811年从喀山大学毕业并且获得硕士学位时才18岁，留校后23岁时就成为教授， 34岁时成了喀山大学的校长。
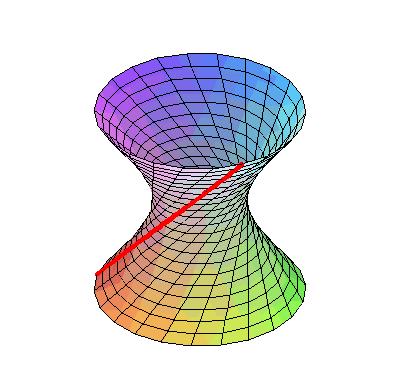
1826年2月，他在喀山大学物理数学系的一次学术会议上，作了题为《附有平行线定理的一个严格证明的几何学原理之简述》的学术报告，在报告中他阐述了一种“虚几何学”存在的可能性。这“虚几何学”就是非欧几何，这一天后来被公认为非欧几何的诞生之日。