数学|1979年高考数学真题，求数列前n项和的最大值，学霸表示真简单学霸

文章图片

文章图片

文章图片
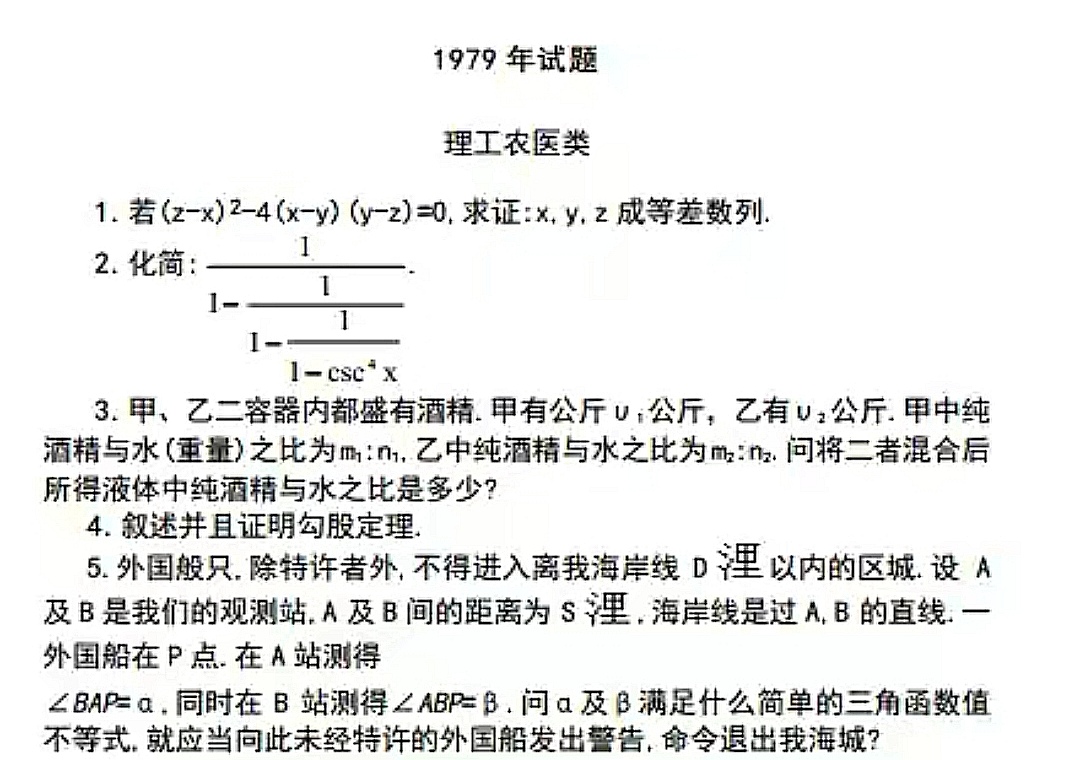
1979年是恢复高考的第三个年头，当年高考数学卷的题型设置与前一年有略有不同，并且从这一年开始，数学试卷开始区分为理科卷(即理工农医类)和文科卷(即文史类) 。在当年的两套数学试卷中，不仅题目的难度不一样，题量也不一样，理科卷共有10道题，而文科卷只有8道题。
本文和大家分享的就是当年理科卷的第9题，题目见下图。这道题是考查等差数列的判定以及前n项和的最大值。从现在的角度来看，本题的难度不大，甚至不少高一学霸直言真简单。不过，这道题的计算量相对还是不小，还是有一些同学出现了计算错误的情况。
回到题目。要求数列前n项和的最大值，那么需要先求出数列的通项公式。本题求解通项公式比较简单，只需将第n项利用对数的运算法则计算出来即可，最终得到an=2-(n-1)lg2/2 。
从这个通项公式可以看出来，该数列是以2为首项，以-lg2/2为公差的等差数列。
接下来再求数列前n项和的最大值。
求最大值有两个方法。
【数学|1979年高考数学真题，求数列前n项和的最大值，学霸表示真简单】第一个方法就是从数列的项入手。
通过通项公式可以看出，该数列是一个逐项递减的等差数列，那么要求前n项和的最大值就只需找出由正转负的那一项即可。也就是说，如果该数列的第n项的值为正数，但是第n+1项的值为负数，那么此时的前n项和就是最大的。所以接下来就需要找到这个n的值。
根据上面的分析可以知道：an≥0且a(n+1)＜0 ，即2-(n-1)lg2/2≥0 ，且2-nlg2/2＜0 ，解得13.2＜n≤14.2 。
因为n为项数，所以n只能为正整数，即n=14 。所以前14项和是该数列前n项和的最大值，求出S14即可。
第二个方法就是先求出前n项和Sn ，再研究Sn取最大值的情况。
常用的等差数列求和公式有三个，即：
Sn=n(a1+an)/2=na1+n(n-1)d/2=-dn^2/2+(a1-d/2)n 。第三个公式就经常用来求等差数列前n项和的最值问题，因为这个公式得到的表达式可以看成是一个关于n的二次函数，所以后面按照二次函数的最值问题求解。
另外，在本题中，当n=13.78是S最大，但是n只能为正整数，不可能为小数。那么n究竟应该取多少时Sn最大呢？Sn可以看成是一个开口向下的二次函数，那么越靠近顶点的点函数值越大，而越靠近顶点的点的横坐标越接近对称轴，而最接近13.78的整数为14 ，即当n=14时， Sn最大，然后将n的值代入Sn的公式即可求出最大值。
本题的难度并不大，只要能够辨别出该数列为等差数列，后面按照等差数列的常用性质求解就可以了。