「」自然常数e到底自然在哪

文章图片

文章图片

文章图片

文章图片

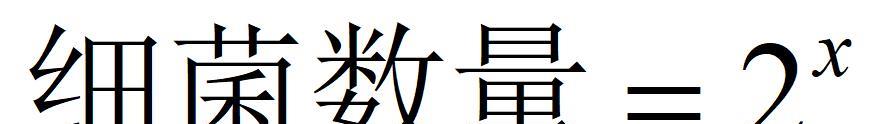
文章图片

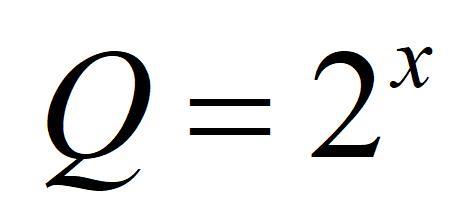
文章图片

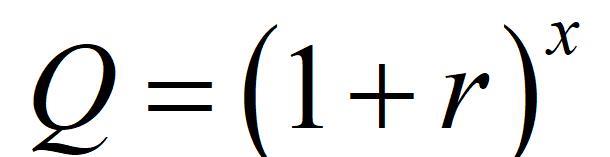
文章图片

文章图片

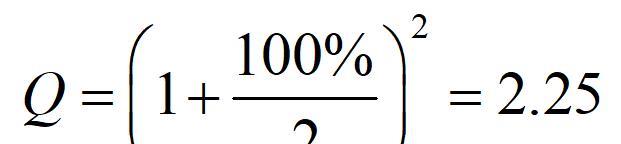
文章图片

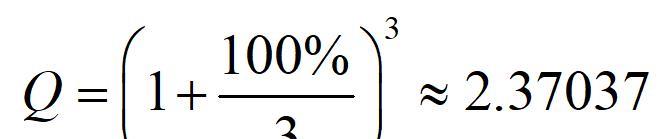
文章图片

文章图片

文章图片

文章图片

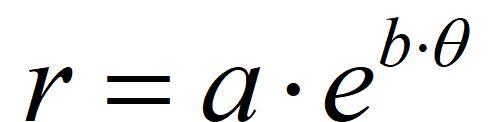
文章图片

文章图片

奇妙の自然常数e
在中，通过对飞蛾运动轨迹的简化表达得到了与自然常数e 相关的等角螺旋线。自然常数e 确实是一个奇妙的数字，这里的e 并不仅仅代表一个字母，它还是一个数学中的无理常数，约等于2.718281828459 。
但你是否有想过，它到底怎么来的呢？为啥一个无理数却被人们称之为“自然常数”？
说到e ，我们会很自然地想起另一个无理常数π。 π 的含义可以通过下图中的内接与外切多边形的边长逼近来很形象的理解。
(图片来源: betterexplained)
假设一个圆的直径为1 ，其外切与内接多边形的周长可以构成π 的估计值的取值范围上下限，内接与外切多边形的边越多，取值范围就越窄，只要边数足够多，取值范围上下限就可以越来越逼近圆周率π。 π 的手动推导过程详见：《古人是如何寻找到π的？》
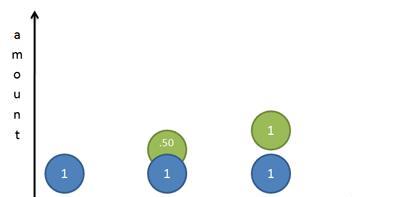
如果说π 的计算很直观，那e 呢？所以在此也用一种图解法来直观理解e 。