两个向量的数量积为什么会是数量向量乘法计算公式介绍 _知识分享

上几篇《白话高中数学》聊完了向量怎么来的、向量的基本概念，也知道了向量如何进行加法运算，今天我们一起聊聊向量的相乘问题。
从几何角度来说，向量的加法遵从“三角形法则”和“平行四边形法则”，也知道向量相加遵从加法交换律、分配率和结合律，那根据这个规则，如果有三个AB向量相加，就会是这样：

文章插图
这种计算称为向量的数乘，也符合我们的基本认知，因为我们熟悉的数字运算就是这样子：n个数相加，就等于这个数乘以n 。
搞清楚了向量的加法和数乘，接下来就必须学习下向量相乘的问题。
两个数相乘还是一个数，那两个带有方向的向量相乘会得到一个什么结果呢？
我们的中学课本给出了一个向量相乘的公式，称为向量的数量积，它说两个向量相乘，其结果是一个数量，没有方向。
也就是这个公式：

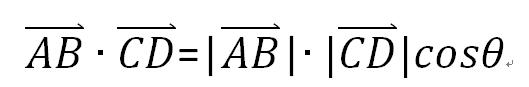
文章插图
其中这个角是指两个向量之间的夹角。
用文字解释就是：两个向量的数量积等于两个向量的“模”相乘，然后再乘以两个向量之间夹角的余弦。
这看起来是一个很奇怪的定义，对不对？
首先两个带有方向的量相乘，得到的结果只是一个数量，方向却凭空消失了？这样显得很神奇不是吗？
它至少颠覆了我们最朴素的认知，觉得这里面肯定有蹊跷。
第二，两个有向线段相乘只是让它们之间的长度相乘，得到一个数也就罢了，还牵涉到两个有向线段夹角的余弦值，这个更让人觉得莫名其妙。
对的，就是有这种莫名其妙的感觉。
两向量相乘的数量积为什么这么定义？有什么原因？这样定义的意义是什么？
一系列问题萦绕在脑中，挥之不去。
课本的解释很简单，它用了物理上一个斜方向的力拉动一个木块，最后木块移动了一段位移，说力和位移这两个向量的数量积就相当于力在水平方向上的分量对木块做的功。
这解释多少有点牵强，它们之间八竿子打不着?。?
用作用力的分量和位移乘积我还可以理解的，但方向去哪儿了？为什么会凭空消失？
最让人迷惑的是我们的数学老师，他们会非常卖力的拿这个课本上的物理现象类比，进行数学课堂上的讲解，当看到同学们迷惑的眼神时，自己也会显得不那么自信，但最后说出的却是“这么简单的问题你们怎么就不明白呢？”这样一句胡话。
可是我就是不明白呀，你要想让我明白，最起码你得告诉我，它们相乘之后的方向去哪了吧？
这个问题至少在中学课堂中没有得到让人满意的回答。
这个问题的最后结局一般是这样：老师告诉你，向量的数量积就这么规定的，你记住就行了。
别的不说，“向量的数量积就是这么规定的”这句话还是相当靠谱的。
老师虽然没有告诉你为什么这么规定，但他至少告诉了我们问题的实质，其实就是数学上“规定”的问题。
但为什么这么规定，大部分老师没有说。即使有进一步解释的，也是采用大学课程里面的向量“点乘”和“叉乘”来云里雾里一番，最后学生只能“哦哦哦”的样子，把问题留待大学课程里再解决。
其实，中学老师的这种解释已经相当努力，相当靠谱了，他们只是没有举出一个让中学生能够理解的例子来辅助学生理解这个定义而已。
为了解释清楚这个问题，我们先退回到对两个数相乘的基本理解：
对于3乘以4，我们的理解其实有两个方向：
1、 3*4，我们可以理解为4个3相加，最后的结果就是3*4=12 。
这种解释没毛病。因为从数轴上看，结果就是如此，符合逻辑，非常直观。
2、我们现在跳出数轴的一维角度，从一个平面的二维角度来看， 3*4也可以代表求一个长和宽分别为3和4的矩形的面积。
OK ，也就是说，对两个数相乘的结果的解释，其实是存在两个不同取向的：
在一维角度得到的是n个数相加；
在二维的角度得到是矩形平面的面积。
【两个向量的数量积为什么会是数量向量乘法计算公式介绍】也就是说，即使是两个只存在数轴上的一维空间的数量相乘，不但可以得到一维空间的数量，也可以扩展得到二维空间的数量。

两个向量的数量积为什么会是数量 向量乘法计算公式介绍

两个向量的数量积为什么会是数量向量乘法计算公式介绍