物理|囚禁于纳米围栏中的量子量子|态密度|原子

本文图片

量子围栏

尘世缤纷设槛栏
春风无处育清寒
蜃楼量子流波影
应是微观作喜欢

1. 引子

曾几何时，当科学技术发展到一定程度，或一位科学家修为到了一定高度，就会开始谈论科学之美。杨振宁先生就经常引用“秋水文章不染尘”一句来描述学问之美，其中味道，读者可去清代篆刻家、书法家邓石如先生在其书房自题楹联：“春风大雅能容物，秋水文章不染尘”那里体会。杨先生是大师，他对科学结构美的鉴赏当然有深度和厚度。我们大多数人，对科学之美的欣赏则主要来自视觉感受：一幅物理图像、一列物理公式，再加上对称、简洁这些元素，便可将科学之美提升到与诸多艺术之美比肩的高度。这是一些科学人嫁接自然与艺术的手法，屡试不爽。

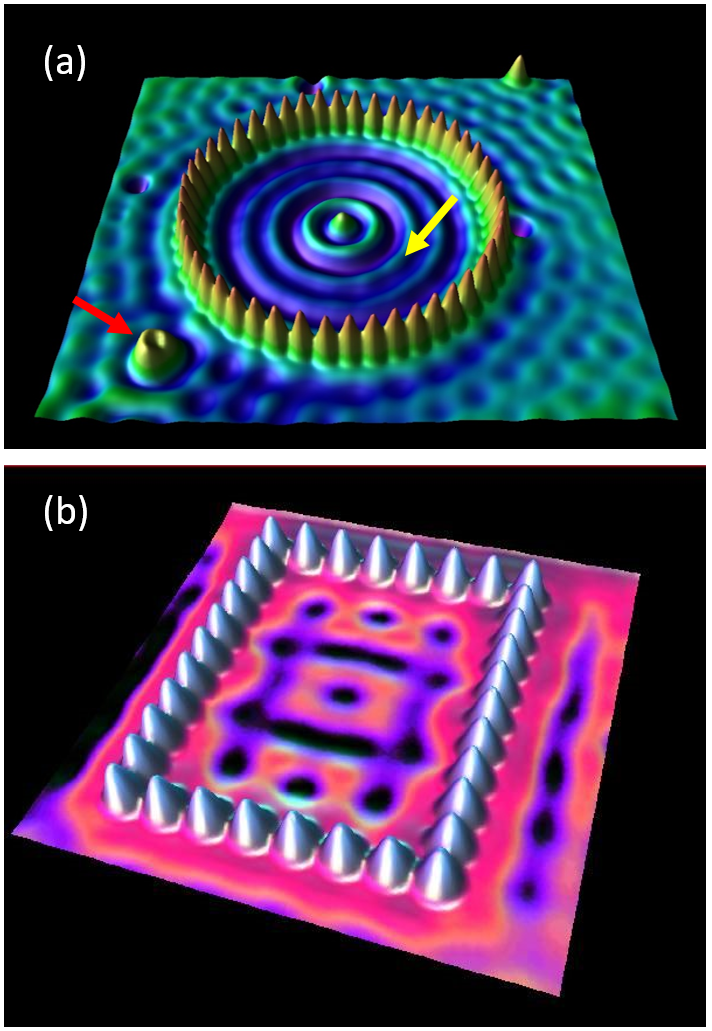
科学的视觉之美已经沁入学者的骨髓，因此常能够引起同行的共鸣与惊叹。话说大约 1990 年代，当时风头正劲的 IBM 公司在加州 Almaden 运行有一个研究中心，颇负盛名。该中心 1993 年发布过一张实验图片，如图 1(a) 所示。图片的视觉瞬时引起巨大轰动，其后亦经久不衰，现在好像已经成为量子物理学的知名印象作品之一。

本文图片
图1. 量子围栏 (quantum corrals) 的 STM 图像。图片 (a) 中，样品是高度洁净和原子级平整的 Cu (111) 表面，表面上有一个圆圈形围栏，乃由 48 个 Fe 原子组成。圆圈平均半径为 7.13 nm ，相邻 Fe 原子之间平均距离 0.95 nm 。红色箭头所指乃一个孤立的 Fe 原子位置，黄色箭头所指乃围栏内形成的“波动干涉”般花样。图片 (b) 乃量子围栏的另外一个例子。
https://www.nisenet.org/catalog/scientific-image-quantum-corral-top-view
https://www.pinterest.com/dbridg66/the-quantum-realm/

众所周知， 1980 年代发展起来的扫描隧道显微术 (scanning tunneling microscopy, STM) 是微结构与电子结构探测技术的一个里程碑。这幅图片描述的是该中心研究人员 M. F. Crommie 等人的一项实验观测结果。这里的样品是高度洁净而有序的金属 Cu 单晶 (111) 表面，呈现清晰的密堆排列。 STM 技术具有在表面操纵单个原子移动的功能。此时，在这一表面沉积上零散的 Fe 原子，然后用 STM 针尖将这些 Fe 原子一个一个移动到某一个区域形成一个圆形或者其它形状的围栏。至此，样品制备即告完成。

接下来即可开始对这个样品表面进行测量。保持针尖和样品之间有一个较低的偏压 (用于防止扫描时针尖导致的原子运动) ，扫描针尖探测到样品表面的形貌 (图 1(a)) 或微分电导之空间分布，从而反映出样品表面的费米面处电子态密度 (微分电导正比于样品表面处的态密度) 之空间分布形态。

这一图片在笔者 (及类似的外行物理人) 看来，有如下几处奇妙特征和迷惑之处：

(1)  好一幅葵花般的围栏形貌，其形态和配色均美妙绝伦，堪称量子物理微观世界的圣品，特别是围栏中心形成蜡烛一般的火炬，虽然不够高。这一围栏乃所谓“量子围栏 quantum corral” ，艺术者则经常称之为量子海市蜃楼一类。

(2)  围栏内部形成了漂亮的波动干涉图样 (黄色箭头所指) ，用直观的方式显示出量子波动干涉物理，令人心动亦意乱情迷。

(3)  孤立的单个 Fe 原子那里，除了其本身的态密度形成火炬外，周围也能清晰看到波动干涉环的图像，虽然远没有围栏内那么明显，就如图中红色箭头所指。

(4)  蹊跷的是， Cu 是金属中难得的优良导体， Fe 也是良好导体。按照金属自由电子理论，样品中的电子应该可以在三维空间随处无阻尼移动。如此，样品表面不应该出现这种看起来是表面波相向而动、形成干涉的场面。这一圈稀稀拉拉 Fe 原子围成的稀疏围栏，竟然将流动的电子束缚在围栏内的表面处，令其不得动弹。这让人费解！

当然，随后，类似的各种量子围栏应运而生，形成各种形态。图 1(b) 给出了一个另外的例子，其形貌同样美轮美奂。

本文图片
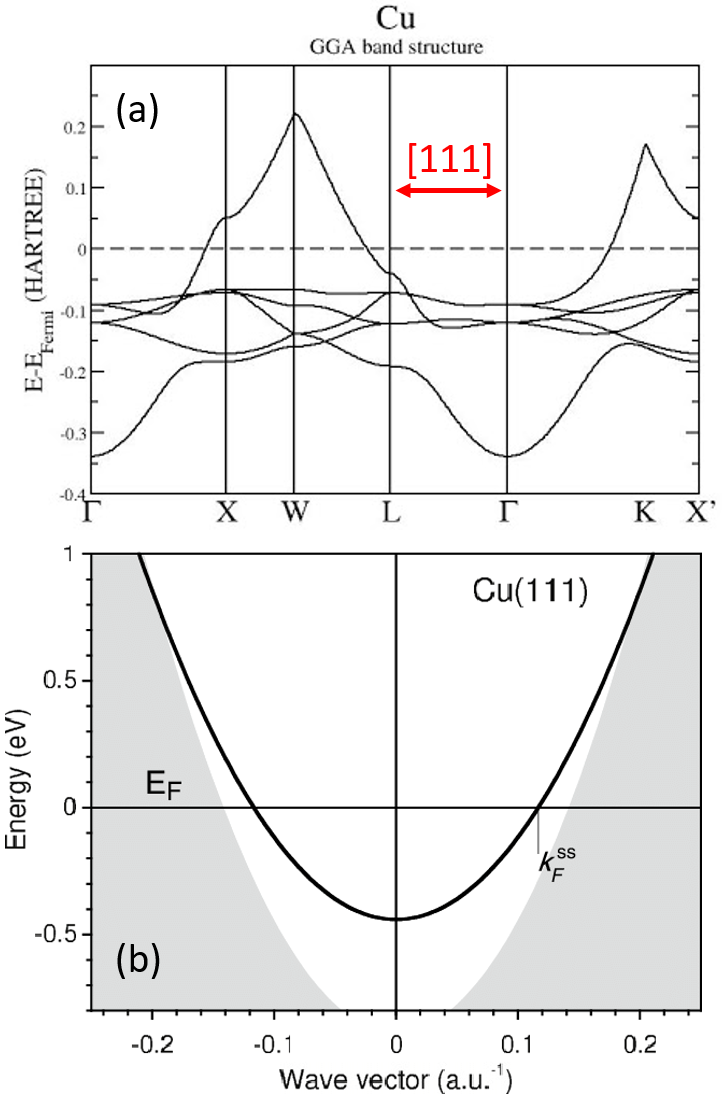
图2. 金属 Cu 的体能带结构 (a) 和 (111) 表面的能带结构 (b) 。体能带中布里渊区的 Γ – L 线段即为实空间的 [111] 方向。可见 Cu 沿着 [111] 方向没有能带穿越费米面，意味着沿这个方向输运存在禁带。图 (b) 显示的 Cu (111) 面的能带结构，其中黑实线代表表面态。在波矢为零处，即 [111] 方向上，费米能级不存在任何态密度，即禁带。分页标题
http://tutorials.crystalsolutions.eu/tutorial.html?td=metalstf=index
https://iopscience.iop.org/article/10.1088/0953-8984/20/30/304209

2. 量子围栏之源

当然，这样的葵花围栏是物理，有必要在这里加以简单说明。事实上， Google 和维基百科中对此有各种细致或简洁的描述版本，大概的物理(不严谨，大致物理图像)可按照下述几条索骥：

(1)  立方体系贵金属 Cu、Ag、Au 的电子结构有一个共同特点：其 (111) 表面存在表面电子态。所谓表面电子态是指费米面处的电子即载流子只能在表面运动，即所谓表面二维电子气，表面层电子无法向深度方向传输。这一效应与我们通常理解的金属导电现象不一致：这是金属啊，怎么会沿某些方向还不能导电了？岂有此理！

(2)  以金属 Cu 为例，表面态的形成机制大约是：参考图 2(a) 所示的金属 Cu 能带结构，可见很多能带穿越费米面，使得 Cu 成为金属。不过，如果仔细去看动量空间布里渊区的 Γ – L 线段即为实空间的 [111] 方向，这个区域没有任何能带穿越，意味着沿这个方向有能隙、是禁带，电子无法沿此方向运动。更为清晰的表达在图 2(b) 所示之 Cu (111) 面费米面附近的色散关系。可见费米面处的波矢 kF  色散不通过坐标原点 [0, 0] ，而这一点正代表 [111] 方向。也就是说，原点 [0, 0] 处的态密度为零：绝缘！
(3)  当然， Cu (111) 表面的电子也不能脱离表面跑到真空或者空气中。因为功函数的束缚，电子不能逸入真空。因此， Cu (111) 表面的电子实际上就是一层平行于表面运动的二维电子气，类似于调制掺杂的界面。
(4)  这些电子气的运动会受到表面台阶、吸附原子等各种不完整结构的散射影响，表现为由于表面二维严格周期性势场被破坏而使电子波动受到散射，会形成各种波动花样。
(5)  Crommie 等发现的 Cu (111) 之量子围栏花样，实质上即围栏内部的电子运动被围栏反射回去，与后续运动而来的电子形成干涉。考虑到电子波动的本质，想象一下水塘之水波涟漪，图 1(a) 所示的干涉花样很容易定性理解。位于围栏中心的“火炬”也是干涉的结果。
(6)  表面上那些单个 Fe 原子周围也有类似物理过程：入射的表面态电子波与被 Fe 原子散射的电子波之间干涉，形成围绕 Fe 原子的驻波，即如图 1(a) 中红色箭头所指。

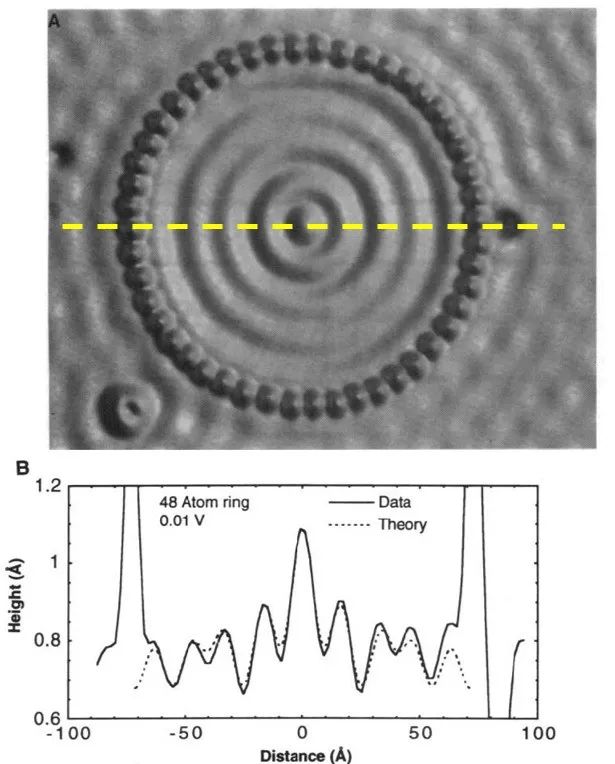
笔者愿意说，物理做到这个份上，感觉物理人就是在凭兴致玩游戏。兴趣所致，不亦乐乎！当然，图 1 所示的图样是经过后期仔细修饰和艺术化处理过，因此成为珍品。一开始发表在 Science 期刊上的图像如图 3 所示，显得简陋而暗淡，虽然物理成分一点也不缺。如果沿图 2 上部图像的黄色虚线进行 profile 线扫描，即得到图 2 下部的高度分布曲线，表达了本征态密度的分布。可以看到，这种波动干涉效应不是个小信号，还是非常显著的。

本文图片
图3. 量子围栏本征态的空间图像。上图 A 的量子围栏花样即图 1(a) ，其中黄色虚线为笔者添加，沿这一虚线线扫描，得到的态密度分布图如下图 B 所示。可以看到，围栏中心原点处 (即火炬处) 态密度最高，然后沿半径向外形成态密度振荡，但振幅越来越小，显示波动干涉效应变弱，态密度变低。 From M. F. Crommie, C. P. Lutz, and D. M. Eigler, Science 262, 218 (1993).

3. 量子尺寸效应

至此，笔者差不多炫耀完大约三十年前物理学的一项成果——量子围栏及其对局域电子态密度的调控。这项开创性的工作开启了利用量子围栏研究量子尺寸效应的大门。

所谓量子尺寸效应，是量子世界最基本的效应之一。它描述的是这样一种现象：当观测对象的尺寸大小和载流子有效德布罗意波长可相比拟时，根据量子力学，这种情况下载流子能量会出现明显的量子化现象，一系列量子化的物理性质即表现出来。除了科学本身的意义之外，量子尺寸效应的应用背景乃与传统硅基器件在超小型化过程中逐渐趋近标度极限有关。随着器件向标度极限趋近，量子尺寸效应的重要性与日俱增，探索此效应亦能够为信息处理和计算提供额外的可能性和可供选择的构架。

很显然，研究量子尺寸效应最简单的办法即将研究对象做到很小，然后评估性能与尺寸之间的关系，看看其如何偏离传统物理机制。不过，这样的研究纯粹是经验和间接的，无法直接和定量体现量子尺寸效应到底呈现什么时空特征。出路在哪里呢？虽然经过日积月累，探测量子尺寸效应的手段和方法已经有很多，但 STM 看起来正在成为最合适的手段之一：STM 扫描隧道显微术不仅可获得样品表面 (通常是金属和半导体) 原子级别的形貌，还可以提取它的局域态密度的时空信息。除此之外， STM 的另外一个独具特色的功能——在样品表面进行原子操纵——使得人们可以在样品表面操纵原子来自由地构造某些结构，定量研究量子效应。分页标题

从这个意义上，量子围栏就成为研究量子尺寸效应的择优对象之一类。原因无他，即 STM 配合量子围栏，可以随意制造各种量子尺寸效应的场景，然后实地表征量子围栏中的各种量子干涉、纠缠、关联和其他相关效应。技术上，这种研究只需 STM 一套、巧手一双、有耐心的脑袋一枚，便可以在 Cu、Ag 等 (111) 面上按照 Go – Go – Go 的模式下围棋，从而下出千万种变化、千万种潮流、甚至是宇宙流。

4. 囚禁于围栏的量子

物理上，通常根据尺寸量子化的维数，将量子尺寸效应分为三类：

(1) 一维受限超薄膜 (指薄膜厚度方向) 。
(2) 二维受限纳米围栏和岛 (平面内受限尺寸) 。
(3) 三维受限量子点 (三维受限) 。

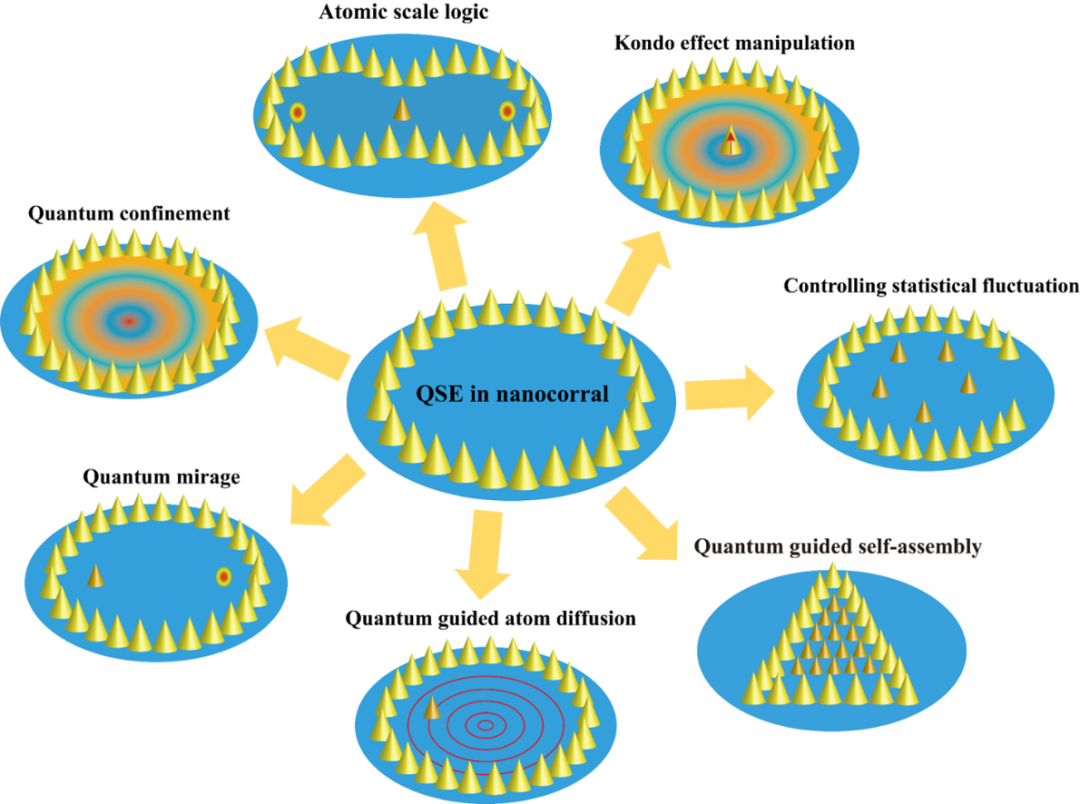
一维薄膜中量子尺寸效应的实验能够追溯到 1966 年。当时发现在铋 (Bi) 超薄膜中，电阻率、霍尔系数和磁电阻均呈现出厚度依赖的现象，而宏观上这些性质应该与厚度无关。此后，薄膜中量子尺寸效应被拓展到光学、相变、超导和磁性等领域。应用方面，薄膜量子尺寸效应能够用来改变磁性薄膜层间耦合作用，并调控巨磁阻。对量子点中三维量子尺寸效应的研究始于 1980 年代末。量子点在医学和屏幕显示上均有广泛应用。此外，在实现量子计算的道路上，量子点也提供了一种可供选择的技术方案。至于二维平面量子受限效应的关注则与器件小型化有密切关联，所以 IBM 这样的商业公司才会对此颇感兴趣。如图 4 所示，笔者在这里将主要讨论纳米量子围栏中的二维量子尺寸效应 [1] 。

如前所述，对量子围栏尺寸效应的开创性研究除了图 1 所示的电子态量子束缚，还有近藤共振的量子海市蜃楼效应。除此之外，量子尺寸效应也被用来引导原子扩散与自组织、控制统计涨落和调制近藤温度。最近的研究工作表明，不依赖于近藤效应的量子海市蜃楼效应能够在费米能附近较宽的能量范围内存在，引起广泛关注。更重要的是，与近藤无关的量子海市蜃楼信号甚至能够比原物态的信号更强，颇有些无中生有的味道。基于这些优点，物理人设想借助于操纵与近藤无关的量子海市蜃楼，可能实现基本逻辑门，例如“非门”、“扇出门”及“或门”等。这里有趣的思路是：海市蜃楼本来就是无中生有，现在竟然可以用无中生有来实现真实的功能，是否有海市蜃楼的感觉！

不妨来看几个例子，看看物理人是如何用“海市蜃楼”来实现物理功能的。这些例子主要出自笔者过去若干年来的摸索性研究数据，虽然结果显得还很简陋和初步。

本文图片
图4. 纳米量子围栏中量子尺寸效应示意图及关联研究示意图 [1] 。

4.1. 原子扩散

第一个例子是原子在围栏内扩散行为的量子限域效应。

表面物理很早就告诉我们，晶体表面如果存在一个原子，只要赋予其足够动能，它就会在表面进行无规随机行走。此为经典原子扩散行为，类比于宏观的布朗运动行为。怎么能够在面心立方金属 (111) 表面上的量子围栏中实现扩散行为的观测呢？最简单直接的做法是：

(1)  选择一个合适的金属 (111) 表面。这里选择 Ag 而不是 Cu 的 (111) 面作为表面；
(2)  选择一个实验温度，一般是液氦温度；
(3)  选择一类金属原子在 Ag (111) 表面构建量子围栏。注意，构建围栏的原子必须足够稳定，不能到处行走。可以挑选 Fe 原子组建围栏，因为 Ag (111) 表面上的 Fe 原子扩散势垒较高，在液氦温度下位置足够稳定；
(4)  选择一类金属原子作为扩散示踪原子。这种原子在 Ag (111) 表面上应该很容易随机扩散，即扩散势垒很低。如 Gd 原子在液氦温度下其表面扩散能力依然很强。

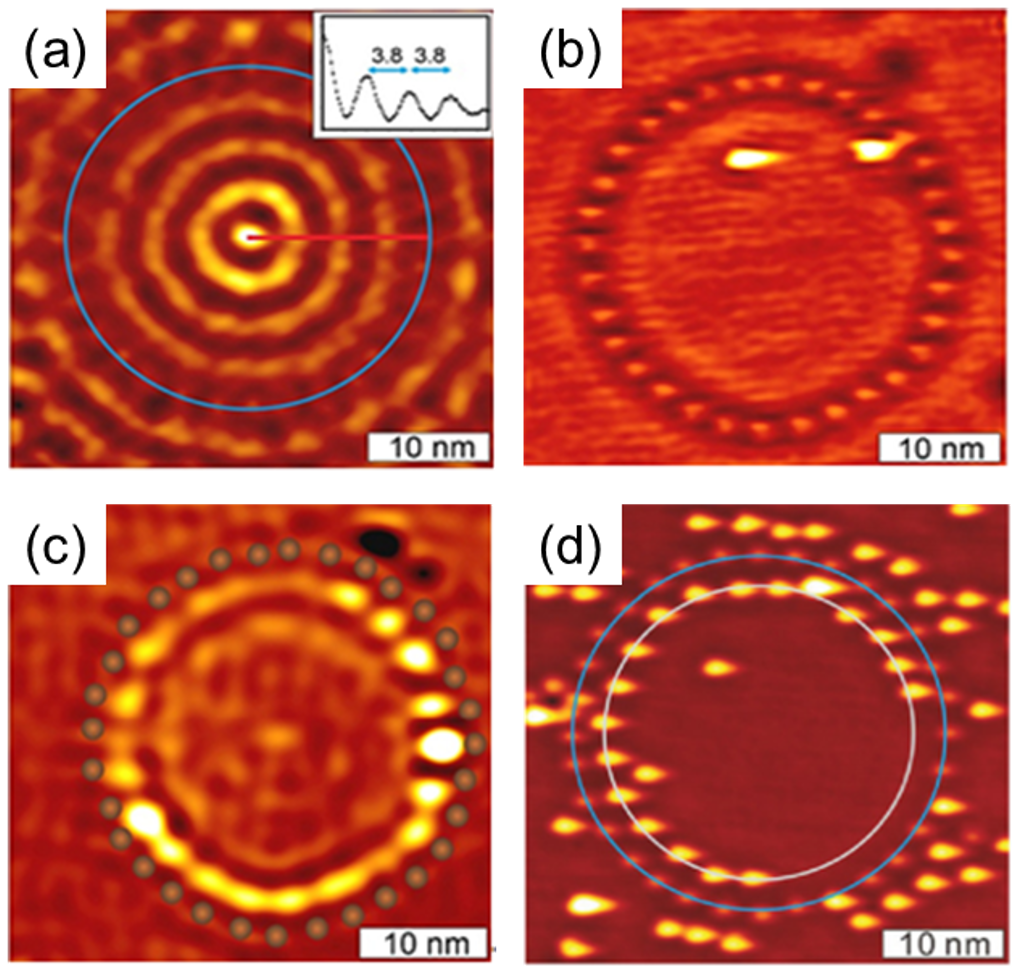
本文图片
图5. 用量子围栏研究量子受限下的原子扩散。 (a) 单晶 Ag (111) 上由 32 个 Fe 原子构建成的、直径为 30 nm 的圆形围栏。围栏内部的电子本征态密度振荡分布 (即量子波动干涉所致的干涉环) 清晰可见 (见插图) ，干涉环间距大约 3.8 nm ，干涉环振幅由中心向外不断减弱。 (b) 两个 Gd 原子 (两个耀斑点即为其位置) 通过电子束蒸发沉积到围栏内，相距大约 7.0 nm 。 32 个 Fe 原子构成的围栏衬度清晰可辨。 (c) 在不同时间内随机采集 500 多幅图像，然后将这 500 幅图像叠加起来，就形成了这两个 Gd 原子的位置概率分布图。这里，亮度越高表示此处 Gd 占据的概率越高。仔细辨认，可以看到 Gd 原子分布呈现三个圆环，越靠近 Fe 原子围栏，圆环亮度越高。越靠近中心的圆环衬度越暗，难以分辨。 (d) 在围栏内部放置 20 个 Gd 原子，一段时间后可以看到这些 Gd 原子会在靠近围栏内测形成一个不闭合的圆环 (图中用高亮的细线将环连起来，以便辨认；外侧的蓝线标识的是 Fe 原子围栏) 。结果来自文献 [Phys. Rev. B 87, 085415 (2013)] 。分页标题

满足了上述四个条件，就可以开始进行实验了：

(1)  首先在 Ag (111) 表面上沉积若干 Fe 原子，并利用 STM 操纵 32 个 Fe 原子形成一个围栏，如图 5(a) 中的蓝色圆环所标识。这个围栏在实验温度下高度稳定。

(2)  测量围栏内的本征态密度分布，即得到类似于图 1(a) 的干涉花样，其线扫描曲线作为插图显示。
(3)  在围栏内放置两个孤立的 Gd 原子。不同时刻去探测它们时，它们的位置是不同的，显示出它们在样品表面行走，即扩散。某一时刻成像显示于图 5(b) ，其中的高亮点即为 Gd 原子，而圆环链状的衬度即 Fe 原子围栏。
(4)  在不同时间测量获得 500 多幅 Gd 原子的位置图像，并将它们叠加起来形成一幅位置概率分布图，如图 5(c) 所示。可以看到围栏内三个链状圆环衬度，越靠近 Fe 围栏的链状圆环衬度越高，表示 Gd 原子倾向于这个圆环位置。每个圆环上的衬度是分立的链状，表示 Gd 原子最倾向于这些位置。
(5)  对应分析可见， Fe 原子围栏内 Gd 原子扩散的位置概率分布与围栏内电子局域态密度位置分布一一对应。

上述实验清晰显示， Gd 原子扩散行为受到了纳米围栏中二维量子尺寸效应的调控。靠近 Fe 围栏的最外圈轨道处拥有最高的 Gd 原子扩散概率。

此时，如果有更多Gd 原子沉积到 Ag 衬底上，它们应该会优先占据这个最外圈轨道并形成环状结构。为了验证这一点，让更多的 Gd 原子被沉积到纳米围栏中，并逐步降低样品温度，以最终“冻结”住 Gd 原子的随机行走。确实，如预期的那样，大部分 Gd 原子优先占据靠近围栏的最外圈轨道位置，形成了环状原子结构，如图 5(d) 所示。如果继续增加围栏内的 Gd 原子数目，将能形成理论预言的“量子洋葱”结构。

本文图片
图6. 三角形纳米围栏中的原子结构。 (a) 三角形围栏内的费米能级附近局域电子态密度图。 (b) 三角形围栏的方向对内部 Gd 原子六角结构方向的调控。注意到，这里的态密度分布呈现的三重对称性并非源自 Ag (111) 面的 Ag 原子排列之六重对称性排列，因为态密度分布图中的振荡周期 (特征尺度) 比 Ag (111) 面的原子间距大得多。 (c) 取自文献的几个实验观测结果，显示出围栏对称性对围栏内局域电子态密度形态的调控 (https://www.pinterest.com/pin/143130094392366755/) 。

4.2. 围栏对称性

如前所示的量子限制效应还可以通过更多花样展示出来。这里的第二个例子是对称性调控。通过构建不同于对称性的 Fe 原子围栏，可以显著调制围栏内的态密度形态。

实验用 Fe 原子构建了一个三角形的纳米围栏，如图 6(a) 的三角形实线所标识。可以看到，体现量子尺寸效应的局域电子态密度分布也呈现出三角 (六重) 对称性，完全不同于圆形围栏的形状。注意到，这里的六重对称性可不是 Ag (111) 表面原子的六重对称排列，因为其尺度差得远了。这完全是波函数干涉的效果。

如果在围栏内沉积足够多的Gd 原子后，经过一段时间随机行走和扩散，这些原子最终会排列成六重对称性，形成六角超晶格结构。再说一遍，这里的对称性与 Ag (111) 表面原子的排列对称性无关，因为如果我们改变三角形纳米围栏方向的取向，其内部由量子尺寸效应引起的局域态密度分布方位也会变化，导致随后沉积其上的 Gd 原子六角结构方向变化，如图 6(b) 所示，奇妙之处自不待言！

在大量类似实验之列，这两个例子表明了纳米量子围栏内的二维量子尺寸效应可以调控内部原子的扩散和生长行为，可以用来构建奇特的原子结构。

4.3. 抑制统计涨落

我们在描述这两个实例时，看起来好像驾轻就熟、像玩游戏似的。实际上，且不说搭建量子围栏本身就很困难，往那么小的量子围栏中沉积确定数目的 Gd 原子大概也是几乎不可能的事情。既然如此，倒不如就另起炉灶，看看能不能顺势而为，关注一些可以关注的科学问题。

既然实验无法精确控制围栏内部 Gd 原子准确数目，那就只好按照 Gd 沉积生长平均速率计算出生长时间来估算单位面积的 Gd 原子数，然后统计控制每个 Fe 原子围栏内的 Gd 原子数目。我们的实验大概按照如下逻辑来实施：

(1)   在一个足够大的 Ag (111) 样品表面构筑很多 Fe 原子围栏，形成一个围栏阵列，如图 7(a) 中的圆环链状图案所示。当然，围栏的直径倒可以根据需要控制。

(2)   在表面沉积设定数目的 Gd 原子，然后对表面进行成像统计，看看每个围栏内有多少 Gd 原子。分页标题
(3)   的确，阵列中不同围栏中存在的 Gd 原子数目有很大涨落，如图 7(a) 所示。
(4)   如果围栏尺寸足够大、Gd 原子数足够多，那围栏内 Gd 原子数的涨落相对值就不显著。随着围栏尺寸减小到直径只有纳米尺度， Gd 原子数少，涨落就非常显著，如图 7(a) 所示左下角的一个围栏内就是空的。

的确，由于量子围栏构建了一个很高的势垒，围栏内的 Gd 原子即便找不到能量很低的位置，但也无法逃逸出围栏，而外面的原子也无法偷渡越境进入围栏。这才是 Gd 原子数展现巨大涨落的原因。那么怎么能够抑制这种涨落呢？最简单直接的方法便是将围栏打开一个口子，允许自由进出，看看会是怎么样的结果。

果然，如果构建一个带开口的围栏阵列，情形就变得截然不同。留一个开口，就能实现围栏内原子数可控，也就是说能抑制统计涨落。如图 7(b) 所示，所有围栏内 Gd 的数目都是 3 个，意味着这个尺寸 (直径 8.5 nm) 的围栏内就只能承载 3 个 Gd 原子存在。这是量子尺寸效应的绝妙体现，令人震慑，相关细节可参见文献 [Phys. Rev. B 90, 045433 (2014)] 。

好！现在来看围栏尺寸效应。采用不同直径的开口围栏，可实现不同 Gd 原子数目的定量捕获，如图 7(c) 所示。围栏越大，能捕获的 Gd 原子数目越多，这是其一。其二，围栏内 Gd 原子倾向于排成正多边形，并且存在四边形和五边形这样的明显不同于 Ag (111) 表面六角晶格的形状，这也证明围栏内的量子尺寸效应。

为了进一步验证定量原子捕获的稳定性，我们系统研究了开口围栏直径与捕获 Gd 原子数的关系，如图 7(d) 所示：Gd 原子数与 Fe 围栏直径呈台阶状，并且较宽台阶给了较大围栏直径选择空间和容错性。很显然，这样漂亮的台阶结构显示了结果的显著性，值得仔细回味。这里，令人疑惑的是围栏捕获 1、2、3、4、5、7 个 Gd 原子的情形都被观测到，但捕获 6 个 Gd 原子的情形没有出现。也许可以这么来理解：如果 6 个 Gd 原子在围栏内形成了正六边形，由于 Gd – Gd 原子之间是吸引势，从能量上应该驱动第 7 个原子从围栏外部进入到六边形中心，使得体系总能量更低。

这一组结果表明至少两点：

(1)   从实验和理论上验证了精确可控的原子捕获归功于开口围栏中量子尺寸效应产生的自我调节过程：如果捕获的 Gd 原子数不足，围栏会自发地从外界捕获原子。如果围栏内有了过多原子，则多余原子会被排斥而逃逸出去，从而实现围栏定量捕获原子的效应。

(2)   应用上，可利用不同直径开口围栏内的二维量子尺寸效应来构建单原子精度的原子结构，实现最大限度抑制原子数目统计涨落，实现局域结构控制。

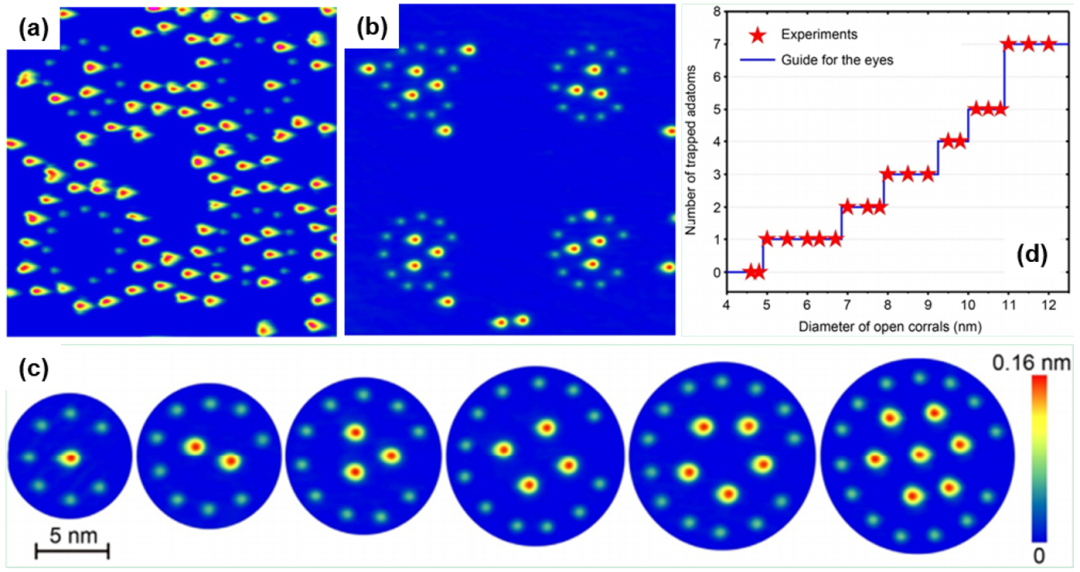
本文图片
图7. 量子围栏中尺寸效应的涨落与抑制。 (a) Fe 原子封闭围栏阵列及其内部存在的 Gd 原子图像，显示原子数目巨大涨落，左下角的围栏内甚至没有 Gd 原子。 (b) Fe 原子的开口围栏阵列及每个围栏捕获了等量的 Gd 原子 (3 个) 。 (c) 不同直径开口围栏内的 Gd 原子排列，呈现出点、线、三角形、四边形、五边形和占心六边形形态。图中量子围栏由小的实心亮点离散圆环 (Fe 原子) 构成、大的亮点为 Gd 原子。 (d) 不同尺寸开口围栏中捕获不同数目原子的台阶状依赖关系，注意没有 6 个原子的台阶。详细内容参考文献 [Phys. Rev. B 90, 045433 (2014)] 。

5. 近藤物理

行文至此的所有量子尺寸效应实验，所关注的还只是量子围栏中外来原子 (例如 Gd) 与 Ag (111) 表面态的相互作用。更深刻的物理研究工作还可以有很多，例如凝聚态物理中知名的近藤 (Kondo) 效应即属其中之一。

众所周知，近藤效应描述的是磁性杂质的局域自旋与传导电子之间的自旋相关散射。在近藤效应中，有一个特征温度——近藤温度，它能够反映磁性杂质的磁性状态。这里为了方便说明问题，姑且假设磁性杂质自旋 S = 1/2 (当然，近藤效应所描述的磁性杂质自旋并不局限于 S = 1/2 ) 。当系统温度远低于近藤温度时，磁性杂质与周围传导电子发生的自旋相关散射较强，形成一个多体效应的自旋单态，即 S = 0 。通俗的理解亦可称之为磁性杂质自旋被屏蔽掉了。当系统温度远高于近藤温度时，磁性杂质与周围传导电子发生的自旋相关散射较弱，此时多体自旋单态无法形成，杂质自旋依然存在。从这个意义上看，所谓“近藤温度”也就是一个能量尺度，衡量了磁性杂质局域自旋与传导电子之间自旋相关散射的强弱。

也很显然，如果我们可以有办法调控传导电子的浓度，也就可以调控此类自旋相关散射。电子浓度越高，就越容易屏蔽磁性杂质的自旋。这就是物理人经常讨论的“磁性杂质的自旋屏蔽与费米能级处的电子浓度 (也就是态密度) 密切相关”的通俗说辞。换句话说，近藤温度必定与样品的费米面处态密度密切相关：态密度越高，则近藤效应中的近藤温度就越高。调控态密度，即可调控近藤温度。分页标题

这里的物理已经呼之欲出：纳米量子围栏正好可以调控围栏内费米面处的电子态密度，对吧？！所以，纳米量子围栏正好可以调控近藤系统的近藤温度，对吧？！

在实验测量上，低温扫描隧道显微镜则提供了一种研究近藤效应的有效手段。由于磁性杂质与传导电子的散射产生了一种共振现象即近藤共振，近藤效应使得在磁性杂质上方测得的隧道谱在费米能级附近呈现出具有一定宽度的峰或谷，其宽度反映了近藤温度的高低。

具体到一个有限尺寸体系而言，其费米态密度就有体态费米态密度与表面态费米态密度之分。利用体态密度来调控近藤温度的物理已众所周知，然而表面态是否与近藤效应密切联系，或者说表面态是否参与近藤效应调控却并不明确。这一问题历史上曾经有过一段时间的争议。

看君阅到此处，应该更加明了用量子围栏来研究近藤效应的价值：因为围栏内的量子尺寸效应就是针对表面态密度的，所以这样的研究有望澄清表面态密度是不是与近藤效应有密切联系，或者说表面态密度能不能参与调控近藤效应。这样的一个物理系统，可以算是踏破铁鞋无觅处，似乎就是为了研究表面态物理而生的。

我们高兴的是，这一争议不久前得到消解，详细结果可参见文献 [Phys. Rev. B 97,035417 (2018)] 。这里，我们只给出简洁的描述：

(1)   构建一个系统：在足够大的 Ag (111) 表面构建不同的 Co 原子围栏，如图 8(a) 和 (b) 所示。其中 (a) 中的围栏中心有一个 Co 原子， (b) 中就没有。这样的两个系统，中心有原子的即形成一个近藤体系，中心空的围栏即不是。

(2)   现在对 (a) 中围栏中心的 Co 原子实施 STM 隧道谱测量，得到隧道谱的近藤共振宽度 w (量纲为 meV ，除以玻尔兹曼常数即得近藤温度) 。针对一系列不同尺寸 (半径为 r ) 的围栏，测量其中心 Co 原子的近藤温度 w ，得到 w  与 r  的关系，如图 8(c) 所示。可以看到， w (r ) 呈现的是一条衰减振荡曲线。
(3)   针对围栏中心没有 Co 原子的情况，即不存在近藤效应的情况，可以测量费米能级处的扫描隧道谱，提取其 dI / dV 数据，也就是表面态密度的高低。测量发现， dI / dV  数据与 r 有类似形状的衰减振荡关系，如图 8(d) 所示。
(4)   两者的相似性毫无疑义地证明表面态密度对近藤共振有调控作用。

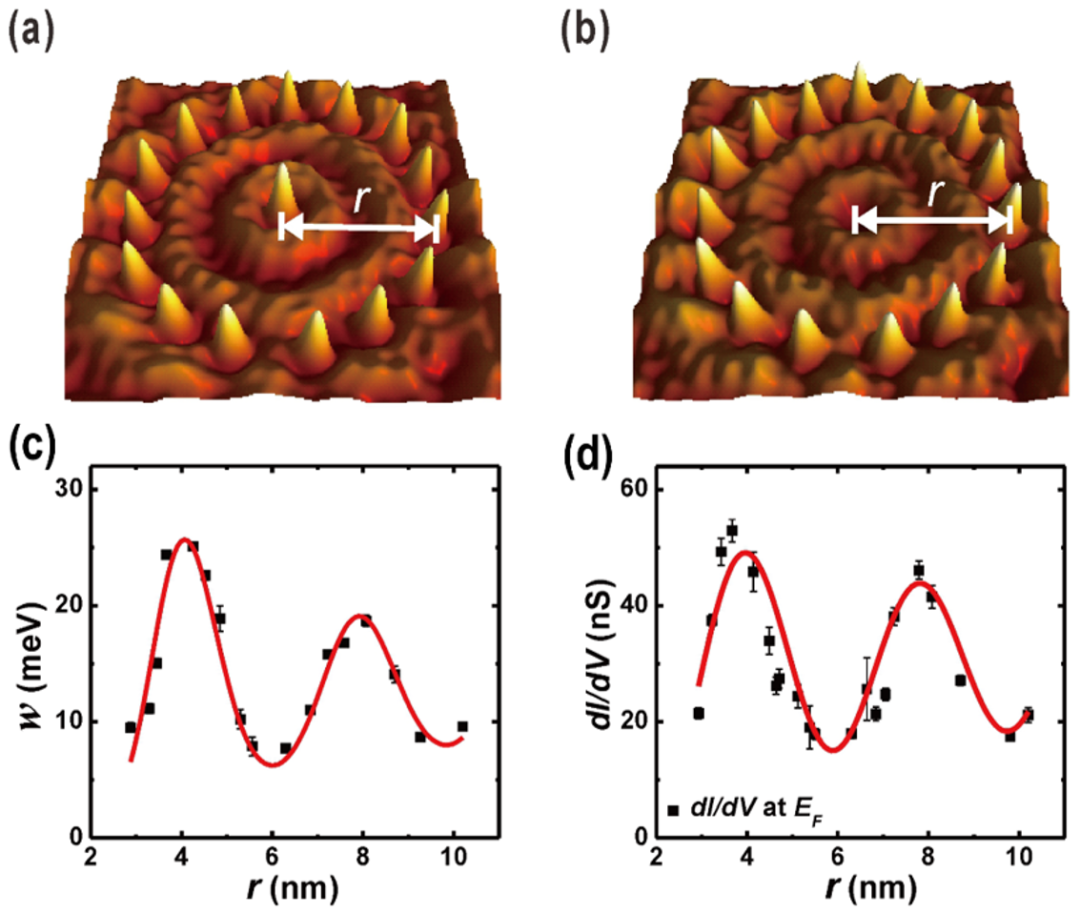
本文图片
图8. 纳米围栏对近藤共振宽度 w  的调制。图 (a) 和 (b) 分别为中心有 Co 原子和中心没有 Co 原子的 Co 原子围栏之 STM 形貌图。 (c) 围栏中心 Co 原子的近藤共振宽度 w  随围栏半径 r 的依赖关系。 (d) 中心为空的 Co 原子围栏的局域表面态密度 (费米能级处的扫描隧道谱 dI / dV 与围栏半径 r 的关系。红色曲线是拟合结果。参考文献 [Phys. Rev. B 97, 035417 (2018)] 。

6. 量子逻辑门

最后，我们展示量子围栏的一类可能的应用，或者说展示一个基于量子围栏的量子信息原型器件。设计并制造这样的器件，使之能够工作和实用，才是我们物理人对消费纳税人劳动的回报。

纳米围栏中的量子尺寸效应并非只是阳春白雪，可以用来构造原子层次的逻辑门器件。这一器件正是基于上一节的“近藤系统”延伸出来。 Manoharan 等人在 2000 年左右观测到诱人的近藤共振量子海市蜃楼现象，展示了纳米尺度下信息传输的可能性。然而，基于近藤效应的量子海市蜃楼只存在于费米能附近。最近，实验观测到，不依赖于近藤效应也可以构造出量子海市蜃楼，且这一效应有相对较高的信息传输效率、能在一个较宽能量范围内进行操控。利用这些优点，原子尺度下的逻辑门就成为可能，诸如“非门”、“扇出门”与“或门”即可构建出来。详细内容可见文献 [Nature Commun. 11, 1400 (2020)] 。

这里的设计思路如下：

(1)   椭圆型围栏的焦点作为信息输入和输出端，其中输入 “1” / “0” 对应于椭圆纳米围栏的一个焦点处原子“有”/“无” ，而输出 “1” / “0” 则通过另外一个焦点处诱发的量子蜃楼之扫描隧道谱强度高/低值来表现。

(2)   “非门”是一个两端结构，正好对应着椭圆纳米围栏中的反转量子海市蜃楼。
(3)   要实现“扇出门”和“或门” ，需要构造一个三端结构。这种三端结构也许有很多方案来构建，但最简单的方案是通过组合两个椭圆围栏来实现，这两个椭圆共用一个焦点，从而构成一个哑铃型的围栏。图 9(a) 所示即为这一概念下的“扇出门” ，其中两个椭圆围栏的共同焦点 A 处原子“无” / “有”分别对应着输入 “0” 和 “1”，如图 9(a) 显示 A 处“无” ，如图 9(c) 显示 A 处“有” 。而输出的分别是焦点 B 和 C 处的扫描隧道谱数值大小，如图 9(b) 和 9(d) 所示。当 A 处没有原子时 (输入为 “0”) ，输出 B 和 C 处的扫描隧道谱值很低 (输出为 “0”)；当 A 处有原子时 (输入为 “1”) ，输出 B 和 C 处的扫描隧道谱值很高 (输出为 “1”) 。这样，输出与输入满足“扇出门”函数关系。分页标题
(4)   把输入和输出的位置交换时，即能得到“或门” 。

需要指出，作为一个器件原型，这里展示的开关信号逻辑阈值大约是 1.5 ，比真实器件的值要小很多。但是，这一比值可通过以下几种方法来提高：这里的实验包含了体态贡献的常数背景，它严重地降低了开关信号比。如果在一个体态很低甚至没有体态贡献的体系中进行实验，有望得到更高的开关信号比。此外，传递函数的幅值依赖于表面态态密度与杂化能；当这两项的强度增加时，也能够得到一个更高的开关信号比。

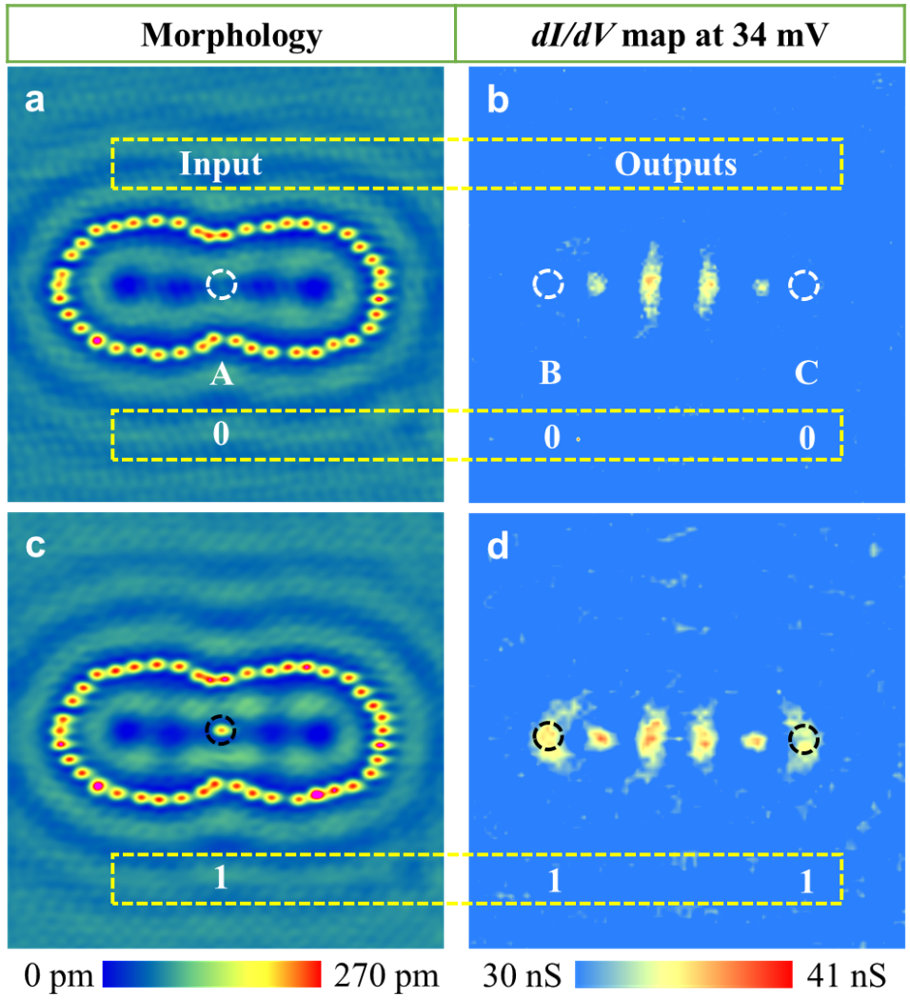
本文图片
图9. “扇出门”器件的构造与工作。器件由两个椭圆形量子围栏叠加而成，它们具有一个共焦点，形成一个特定的哑铃型围栏或称共焦椭圆围栏。 (a) 空的共焦椭圆围栏 STM 形貌图；(b) 相应的 dI/ dV 谱图；(c) 共同焦点 A 处有一个 Fe 吸附原子时，对应的 STM 形貌图；(d) 相应的 dI / dV 谱图。椭圆尺寸为 a = 6.6 nm, e = 0.7 。椭圆围栏焦点由虚线圆圈标出，其中黑色表示 1、白色表示 0 。来自文献 [Nature Commun. 11, 1400 (2020)] 。
7. 展望

行文至此，笔者对看君表示谢意，辛苦您坚持阅读到这里。

本文对近十年来纳米围栏中的量子尺寸效应作了简单而不是很严谨的回顾。纳米围栏中量子尺寸效应的本质是吸附在基底表面的原子能够对表面电子态进行散射。由吸附原子构成的围栏能够将电子态束缚在围栏内，使得围栏内态密度出现振荡。众所周知，电子体系的绝大部分性质由其电子态密度决定，尤其是费米能附近的态密度。因此，除了原子扩散与自组织、原子捕获和近藤效应，可以期待更多与态密度有关的量子现象在纳米围栏中呈现。

利用 Fe 原子在 Ag (111) 表面搭建的椭圆量子围栏，可以展现吸附原子与近藤无关的量子蜃楼，并可进行一些基本逻辑操作。那么，不禁要问，还有没有其它体系能够展现出量子蜃楼现象并进而实现基本逻辑操作呢？有的！应用的问题是大事，值得再啰嗦几句，以作为本文的结语：

(1)   第一类，利用磁性原子在超导基底表面搭建椭圆量子围栏。

如前所述，实验已观察到了与近藤效应无关的量子蜃景，并揭示了其物理机制。这意味着，只要具有特征谱的原子，能被衬底表面电子散射，都应该具有量子蜃景现象。例如，磁性原子在超导衬底表面会有一个特征谱 (超导能隙内) ，即 Yu – Shiba – Rusinov (YSR) 态 [2 - 4] 。早在 2004 年， Morr 等人从理论上给出了磁性杂质在超导衬底表面的量子蜃楼预言 [5] 。然而，目前尚无实验来证实该理论预言。从实验角度来说，超导能隙一般只有几个毫电子伏。要想在这么小的能量范围内探测 YSR 态，需要有足够低的温度。事实上，目前的实验技术已经成功探测到了 YSR 态 [6] ，甚至自旋分辨的 YSR 态也已经被观察到 [7] 。所以，对于磁性杂质在超导体表面的量子蜃楼的观测也指日可待了。
(2)   第二类，利用磁性原子在拓扑绝缘体表面搭建椭圆量子围栏。

实验上制备拓扑绝缘体实际上是最近十多年的事 [8, 9] 。 2014 年， Loptien 等人首次在拓扑绝缘体 Bi2Se3 (111) 表面上用 Rb 原子搭建了一个量子围栏 [10] 。 Loptien 等人的工作表明，在拓扑绝缘体上构造量子围栏是完全可行的。但由于 Rb 原子是非磁原子，对表面态电子散射作用非常弱。如果改用磁性原子来构造量子围栏，其散射作用会比较强，并且对表面态电子的自旋向上和自旋向下的散射作用不一样。因此，还可以得到自旋分辨的相关信息。此外， Fe 原子在 Bi2Se3 (111) 表面还具有特征谱 [11] 。这些都为观察量子蜃楼创造了条件。

(3)   第三类，在二维材料表面搭建椭圆量子围栏。

二维材料是近年来十分热门的材料，因其所展现出来的巨大的应用前景。石墨烯是一种典型的二维材料。在此，我们设想能否对石墨烯单原子空位进行调控，并利用其空位构造一些人工结构，比如椭圆量子围栏。如果该技术能够实现，那将是一个很大的进步。如果不考虑实验技术难题，利用石墨烯空位观察量子蜃景的可行性如下：(i) 空位能对二维电子进行散射；(ii) 空位具有特征谱，即在费米能附近有一个很强的峰 [12] 。其它二维材料可能也具有类似的性质。最后，二维材料在这个方面还有很大的开发空间。

参考文献

[1] 本文主要内容来源于 Quantum size effect in nano corrals: From fundamental to potential applications, Appl. Phys. Lett. 117, 060501 (2020), https://doi.org/10.1063/5.0015542 。涉及到的相关文献均可从中找到，其中没有的文献则在此单独给出。分页标题
[2] Y. Luh, Acta Physica Sinica 21, 75 (1965).
[3] H. Shiba, Progress of Theoretical Physics 40, 435 (1968).
[4] A. I. Rusinov, Journal of ExperimentalTheoretical Physics 29, 1101 (1969).
[5] D. K. Morr and N. A. Stavropoulos, Phys. Rev. Lett. 92, 107006 (2004).
[6] S. H. Ji, T. Zhang, Y. S. Fu, X. Chen, X. C. Ma, J. Li, W. H. Duan, J. F. Jia, and Q. K. Xue, Phys. Rev. Lett. 100, 226801 (2008).
[7] L. Cornils, A. Kamlapure, L. Zhou, S. Pradhan, A. A. Khajetoorians, J. Fransson, J. Wiebe, and R. Wiesendanger, Phys. Rev. Lett. 119, 197002 (2017).
[8] Y. L. Chen, J. G. Analytis, J. H. Chu, Z. K. Liu, S. K. Mo, X. L. Qi, H. J. Zhang, D. H. Lu, X. Dai, Z. Fang, S. C. Zhang, I. R. Fisher, Z. Hussain, and Z. X. Shen, Science 325, 178 (2009).
[9] Y. Xia, D. Qian, D. Hsieh, L. Wray, A. Pal, H. Lin, A. Bansil, D. Grauer, Y. S. Hor, R. J. Cava, and M. Z. Hasan, Nature Phys. 5, 398 (2009).
[10] P. L?ptien, L. Zhou, J. Wiebe, A. A. Khajetoorians, J. L. Mi, B. B. Iversen, P. Hofmann, and R. Wiesendanger, Phys. Rev. B 89, 085401 (2014).
[11] J. Honolka, A. A. Khajetoorians, V. Sessi, T. O. Wehling, S. Stepanow, J. L. Mi, B. B. Iversen, T. Schlenk, J. Wiebe, N. B. Brookes, A. I. Lichtenstein, P. Hofmann, K. Kern, and R. Wiesendanger, Phys. Rev. Lett. 108, 256811 (2012).
[12] M. M. Ugeda, I. Brihuega, F. Guinea, and J. M. Gómez-Rodríguez, Phys. Rev. Lett. 104, 096804 (2010).

备注：
(1)   本文原作者有李启立、曹荣幸、丁海峰三人，他们分别是南京大学物理学院博士后、扬州大学物理科学与技术学院讲师、南京大学物理学院教授。因为微信公众号作者栏的字数限制，只够填写两位作者，故在此特加说明，以示公正。
(2)   本文有公众号编辑参与进行科普化改写。由此产生不严谨、不恰当和错误之处，皆有编辑负责。
(3)   题头小诗乃表达一种对量子围栏的痴迷！
来源：量子材料
【物理|囚禁于纳米围栏中的量子】编辑：观山不易