关于欧拉公式的拓展，可以了解层层宇宙的存在形式和数理特征关于欧拉公式：e^（πi）+1=0

傻大方提示您本文标题是：《关于欧拉公式的拓展，可以了解层层宇宙的存在形式和数理特征》。来源是。

关于欧拉公式的拓展，可以了解层层宇宙的存在形式和数理特征。宇宙|特征|形式|数理|拓展|物质世界---

关于欧拉公式：e^（πi）+1=0，

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

关于欧拉公式的证明，可作如下的图，

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

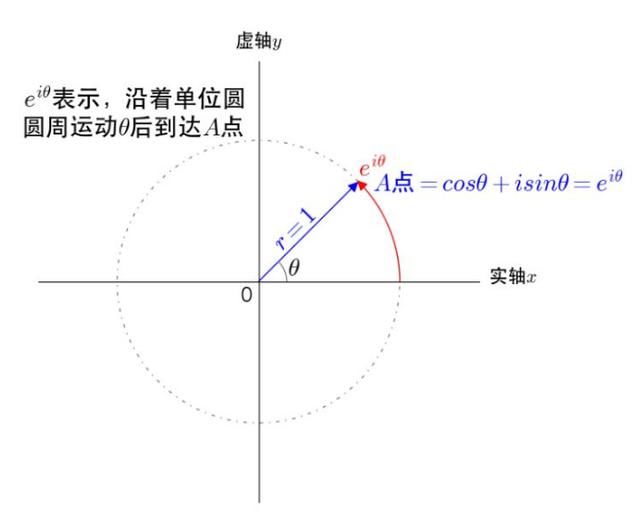
我们可以把e^（θi）当做单位圆的圆周上的点的运动来描述，cosθ+isinθ是同样的复平面坐标系上的点的不通描述，于是：e^（θi）=cosθ+isinθ，可证明当θ=π时，e^（πi）+1=0，成立。

当然，举世闻名的欧拉公式，有很多漂亮的证明方法。

构思都很巧妙。

我们拓展欧拉公式的表达形式，用来表达更高深的客观现象。

或者说用来表达层层宇宙空间的存在形式，

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

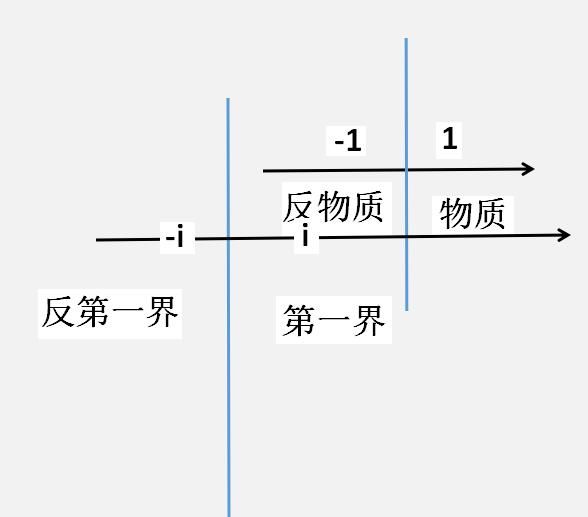
以上这段话，要表达的意思，就1代表物质世界的单位数量特征，-1代表反物质世界的单位数量特征，

那么以1和-1为单位特征的物质世界和反物质世界的总称，对应为第一界，也就是第一物质界，第一宇宙。

在以i和-i为单位数量特征的世界，是和第一界的延伸，

相当于第一界在以i为单位数量特征的世界里，而反第一界在以-i为单位数量特征的世界里；

那么以i为单位特征的第一界和以-i为单位数量特征的反第一界，他们的总称对应第二界，第二物质界，第二宇宙。

依次类推，

注意一点，在第三界里面，对应的j值是一对共轭复数，标记为：j1和j2；

对应的反第三界的单位数量特征是：-j1和-j2；

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

原文如下：

第一界：物质和反物质，1和-1；

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

第二界：第一界和反第一界，i和-i；

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

第三界：第二界和反第二界，j1，j2和-j1，-j2；向量数：2^(3-1);

第四界：第三界和反第三界，k1，k2，k3，k4和-k1，-k2，-k3，-k4；向量数：2^(4-1);

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

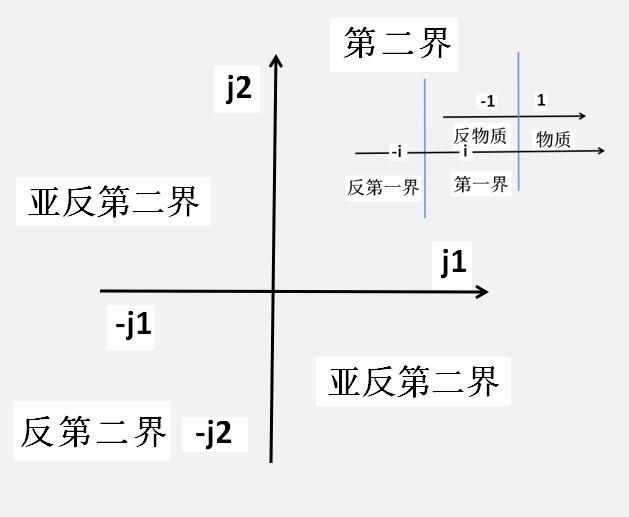
（上图说明，这是一个四个象限的坐标系，第二界只是在第一象限，除了一个反第二界外，增加了两个亚反第二界，）

第4界的情形如下：

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

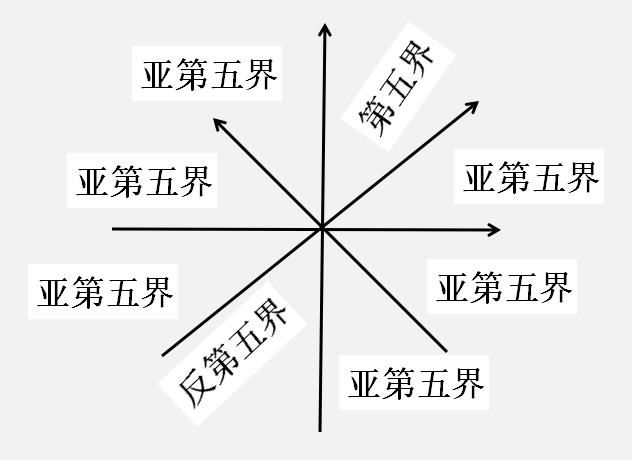
（上图说明，这里有相当的复杂性和重叠性。）

第n界：第三界和反第三界，s1，s2，s3，s4，...，s[2^(n-2)]和-s1，-s2，-s3，-s4，...，-s[2^(n-2)];向量数：2^(n-1);

第n+1界：第三界和反第三界，t1，t2，t3，t4，...，t[2^(n-1)]和-t1，-t2，-t3，-t4，...，-t[2^(n-1];向量数：2^(n);既是：2^n。

这种规律其实就是：太极生两仪，两仪生四象，四象生八卦，八卦生十六卦，十六卦生三十二卦，三十二生六十四卦，以此类推。

宇宙|特征|形式|数理|拓展|物质世界---傻大方小编总结的关键词

至此，相对于物质世界的反物质，他们综合累加起来才属于第一层宇宙，也就是仅在第一届。

而更微观或者更加宏观的宇宙，可以层层探究下去。

大开脑洞了解世界。

这里是给出理解多层宇宙，多层物质世界的一种数学模型。

勿喜轻喷。