基于便利收益模型的PTA 跨期价差分析可以通过已知的工厂利润及注册仓单数

傻大方提示您本文标题是：《基于便利收益模型的PTA 跨期价差分析》。来源是和讯期货。

基于便利收益模型的PTA 跨期价差分析。价差|收益|模型|基差|仓单|pta---

可以通过已知的工厂利润及注册仓单数据进行定价

定价原理

基于便利收益模型的PTA 跨期价差分析。价差|收益|模型|基差|仓单|pta---

商品期货合约的定价通常比金融资产及其衍生品的定价更为复杂，原因在于标的商品具有以下两个特点:一是以消费品和中间产品的形式存在;二是商品具有金融资产的某些特征。从这种意义上来说，标的商品有唯一的均衡市场价格，并且此均衡价格受到投机性储存的影响。基于标的商品的以上两个特点，在商品期货市场传统理论的国内外文献综述中，存在两种最为基本的商品期货定价理论模型--风险溢价模型和便利收益模型。

本文主要讨论便利收益模型在商品期货定价中的应用。便利收益模型是以套利为基础的商品期货定价模型，由Kaldor(1939)和Working(1948)首创。该模型通过当前的商品现货价格和合适的便利收益来对商品期货合约进行定价。因为商品持有者可能会认为，持有商品比持有期货合约能提供更多便利，如果贮存成本为现金形式，而且已知现值为U，商品的便利收益率y则可以由以下关系式来定义:F0eyT=S0e(r+u)T，即F0=S0e(r+u-y)T。

便利收益取决于存货量，并反映了市场对将来能够购买商品的可能性的期望，商品短缺的可能性越大，便利收益率就越高。如果商品的用户拥有大量库存，在不久的将来出现商品短缺的可能性便会很小，这时便利收益率也会比较小。因此，低库存意味着较高的便利收益，反之亦然。另外，Working(1958)、Brennan(1958)和Telser(1958)提出的“储存理论”指出，存货和便利收益之间存在负斜率的、凸的关系。就商品的用途、可存储性及可利用度这三方面来看，商品同时充当了资产和消费品的多重角色，关于商品期货定价模型的不确定性也来源于此。

通过便利收益模型F0=S0e(r+u-y)T我们不难看出，由于无风险收益r通常可以用同业拆借代替，而对于特定商品存储成本u是可知的，那么我们只要知道便利收益y，便能通过已知的现货价格对期货进行定价。同时，由于基差=S0-F0=S0-S0e(r+u-y)T，时间T可以通过现货与期货合约的到期时间求得。因此，我们也可以对基差进行定价，同理也可以对期货合约间的跨期价差进行定价。对于进行期现套利及跨期套利的公司来说，当基差及跨期价差偏离其合理定价时，就存在套利的可能，此时便可通过反向操作实现套利。

实证研究
PTA期货是国内较早上市的期货品种之一，市场相对成熟，所以本次实证研究选取PTA期货为标的。

基于便利收益模型的PTA 跨期价差分析。价差|收益|模型|基差|仓单|pta---

参数的选取

由于PTA现货在华东地区的交易活跃，所以关于PTA产业链的上下游数据，均选取华东地区的价格作为参数。本文我们选取华东地区的PTA现货价格作为现货端(S0)的参数，对应的期货主力合约作为期货端(F0)的参数，华东地区进口PX的价格作为PTA上游的参数，相对应的期货仓单数据从Wind数据库中提取。其中，PTA工厂利润=PTA现货价格-(PX折算进口价格×0.655单耗+600元/吨加工费)。

关于无风险收益r和存储成本u的选取，r选取现货时刻对应的上海同业拆借利率，PTA的仓储费为每天0.4元/吨，可以通过相应的公式折算成u。所有选取的数据时间段为2014年1月1日至2017年3月31日，因为该时段PTA行业处于产能过剩期，大部分产品会首先注册成仓单，在期货盘面出现升水可锁定加工费用的情况下，PTA生产商会选择交割盘面。

参数的观察

基于便利收益模型的PTA 跨期价差分析。价差|收益|模型|基差|仓单|pta---

图为PTA仓单与基差的关系

通过上图可以观察到，PTA期货的仓单数据与期现基差有一定的负相关性，具体是线性还是非线性，需要统计历史数据才能得出。

价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

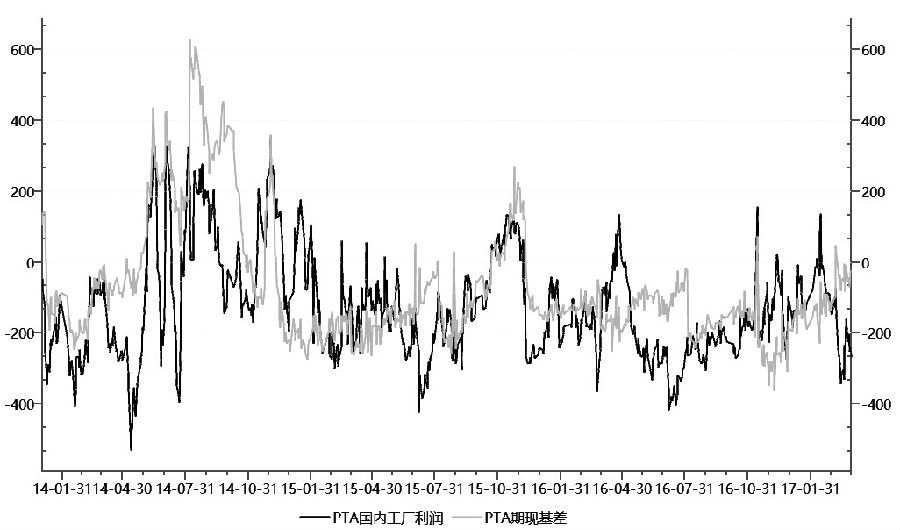图为PTA工厂利润与基差的关系

通过上图可以观察到，PTA国内工厂利润与期现基差有一定的正相关性，具体是线性还是非线性，需要统计历史数据才能得出。

PTA市场有一个非常特别的习惯，即企业常年处于亏损状态，产能过剩，企业生产出来的存货会注册成期货仓单变为仓单库存，在一定程度上代表了PTA的存货情况，并且企业利润可以通过期货市场进行锁定，以防亏损。因此，我们得出这样一个命题:PTA的仓单数量及企业利润在一定程度上解释了期现基差，即S0[1-e(r+u-y)T]。如果PTA的期现基差S0[1-e(r+u-y)T]，能够通过PTA仓单数据(C)及PTA工厂利润(P)进行表示，并且无风险收益r和存储成本u已知，那么就可以得到便利收益y的具体表达式。

参数的分析

已知现货价格为S0，对应的期货合约时间间隔为T，无风险利率为r，贮存成为U，便利收益为Y，得出F0=S0erT+U-Y/eT，期现基差=S0-F0=S0(1-erT)-U+Y，Y=期现基差- S0(1-erT)+U。因此，通过消除时间影响因素的便利收益Y/eT、PTA注册仓单(C)、PTA工厂利润(P)三组数列(每组762个数据)的统计分析，基本能够确定便利收益Y/eT(Y1)与C(X1)、P(X2)解释的函数表达式。

用Matlab以数量C与Y/eT做散点图，如下图(Figure1)所示:

价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

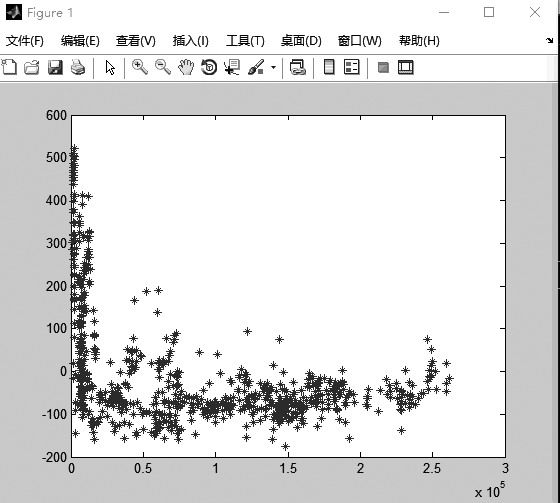
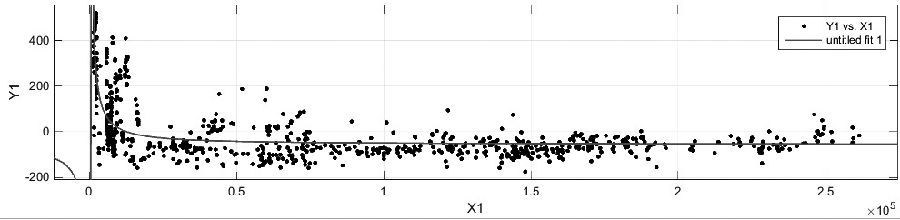
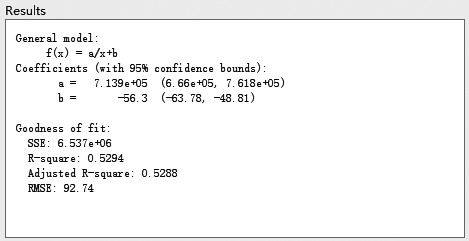
通过观察得知，该函数有明显的反函数性质，即y=a/x+b，通过Matlab拟合如下图所示:

价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

然后，用Matlab以数量P与Y/eT做散点图，如下图(Figure2)所示:

价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

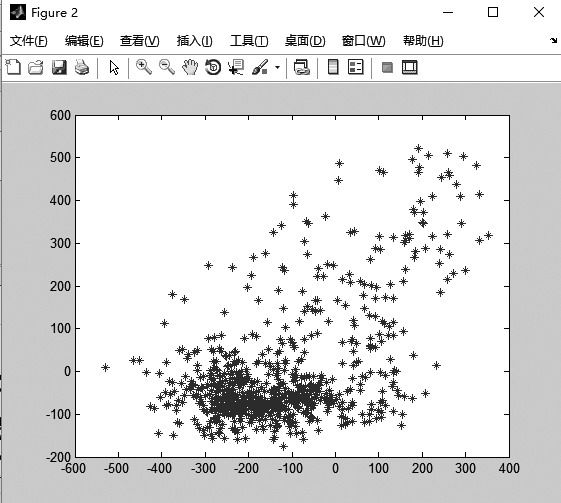
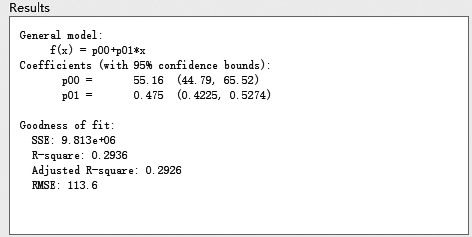
通过观察得知，该函数有明显的线性关系，即y=p00+p01×x，通过Matlab拟合如下图所示:

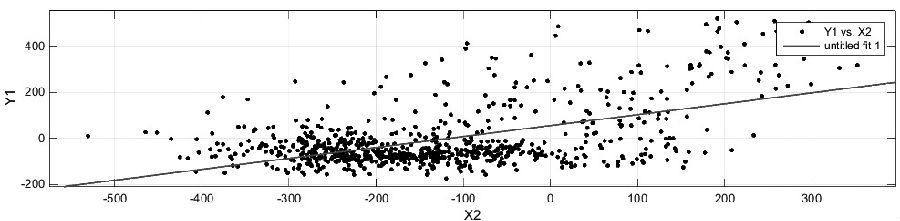
价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

因此，我们不难得出C、P、Y/eT三者的关系式为Y/eT=poo+p01/C+p02×P，通过Matlab拟合如下图所示:

价差|收益|模型|基差|仓单|pta---傻大方小编总结的关键词

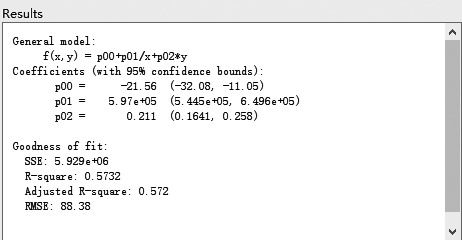
调整后的R方(R squre)达到0.572，解释力度均高于单独考虑C或P的模型，并且同时考虑C和P的模型RMSE均有减少，说明用C和P同时表达便利收益更为合理，最终得出表达式Y/eT=597000/C+0.211×P-21.56。

综合以上分析，通过选取参数，利用计算机软件及统计分析的方法，实证便利收益期货定价模型在PTA期货上能够得到很好的应用。同时，便利收益也能够通过仓单数据及工厂利润进行具体表示，最终得出R方为0.572，具有很高的解释力度。公式显示，仓单与便利收益具有反函数关系，工厂利润与便利收益具有线性关系。因此，我们可以通过已知的工厂利润及注册仓单数据进行PTA基差及跨期价差，该方法甚至可以应用在量化投资领域。不过，由于最终得出的R方为0.572，并不能完全解释便利收益Y，所以关于便利收益的影响因子还需要我们做更深入的研究。

(作者单位:新晟期货)