图片：DobbinSoong
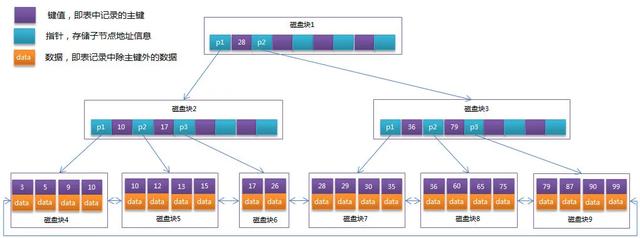
每个节点占用一个盘块的磁盘空间 ， 一个节点上有两个升序排序的关键字和三个指向子树根节点的指针 ， 指针存储的是子节点所在磁盘块的地址 。 两个关键词划分成的三个范围域对应三个指针指向的子树的数据的范围域 。 以根节点为例 ， 关键字为17和35 ， P1指针指向的子树的数据范围为小于17 ， P2指针指向的子树的数据范围为17~35 ， P3指针指向的子树的数据范围为大于35 。
模拟查找关键字29的过程：

1. 根据根节点找到磁盘块1 ， 读入内存 。 【磁盘I/O操作第1次】
2. 比较关键字29在区间（17,35） ， 找到磁盘块1的指针P2 。
3. 根据P2指针找到磁盘块3 ， 读入内存 。 【磁盘I/O操作第2次】
4. 比较关键字29在区间（26,30） ， 找到磁盘块3的指针P2 。
5. 根据P2指针找到磁盘块8 ， 读入内存 。 【磁盘I/O操作第3次】
6. 在磁盘块8中的关键字列表中找到关键字29 。

分析上面过程 ， 发现需要3次磁盘I/O操作 ， 和3次内存查找操作 。 由于内存中的关键字是一个有序表结构 ， 可以利用二分法查找提高效率 。 而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素 。 B-Tree相对于AVLTree缩减了节点个数 ， 使每次磁盘I/O取到内存的数据都发挥了作用 ， 从而提高了查询效率 。
B+TreeB+Tree 是在 B-Tree 基础上的一种优化 ， 使其更适合实现外存储索引结构 ， InnoDB 存储引擎就是用 B+Tree 实现其索引结构 。
从上一节中的B-Tree结构图中可以看到每个节点中不仅包含数据的key值 ， 还有data值 。 而每一个页的存储空间是有限的 ， 如果data数据较大时将会导致每个节点（即一个页）能存储的key的数量很小 ， 当存储的数据量很大时同样会导致B-Tree的深度较大 ， 增大查询时的磁盘I/O次数 ， 进而影响查询效率 。 在B+Tree中 ， 所有数据记录节点都是按照键值大小顺序存放在同一层的叶子节点上 ， 而非叶子节点上只存储key值信息 ， 这样可以大大加大每个节点存储的key值数量 ， 降低B+Tree的高度 。
B+Tree相对于B-Tree有几点不同：

1. 非叶子节点只存储键值信息；
2. 所有叶子节点之间都有一个链指针；
3. 数据记录都存放在叶子节点中

将上一节中的B-Tree优化 ， 由于B+Tree的非叶子节点只存储键值信息 ， 假设每个磁盘块能存储4个键值及指针信息 ， 则变成B+Tree后其结构如下图所示：
文章插图
通常在B+Tree上有两个头指针 ， 一个指向根节点 ， 另一个指向关键字最小的叶子节点 ， 而且所有叶子节点（即数据节点）之间是一种链式环结构 。 因此可以对B+Tree进行两种查找运算：一种是对于主键的范围查找和分页查找 ， 另一种是从根节点开始 ， 进行随机查找 。
可能上面例子中只有22条数据记录 ， 看不出B+Tree的优点 ， 下面做一个推算：
InnoDB存储引擎中页的大小为16KB ， 一般表的主键类型为INT（占用4个字节）或BIGINT（占用8个字节） ， 指针类型也一般为4或8个字节 ， 也就是说一个页（B+Tree中的一个节点）中大概存储16KB/(8B+8B)=1K个键值（因为是估值 ， 为方便计算 ， 这里的K取值为10^3） 。 也就是说一个深度为3的B+Tree索引可以维护10^3 * 10^3 * 10^3 = 10亿 条记录 。
实际情况中每个节点可能不能填充满 ， 因此在数据库中 ， B+Tree的高度一般都在2-4层 。 MySQL的InnoDB存储引擎在设计时是将根节点常驻内存的 ， 也就是说查找某一键值的行记录时最多只需要1~3次磁盘I/O操作 。
B+Tree性质

1. 通过上面的分析 ， 我们知道IO次数取决于b+数的高度h ， 假设当前数据表的数据为N ， 每个磁盘块的数据项的数量是m ， 则有h=㏒(m+1)N ， 当数据量N一定的情况下 ， m越大 ， h越小；而m = 磁盘块的大小 / 数据项的大小 ， 磁盘块的大小也就是一个数据页的大小 ， 是固定的 ， 如果数据项占的空间越小 ， 数据项的数量越多 ， 树的高度越低 。 这就是为什么每个数据项 ， 即索引字段要尽量的小 ， 比如int占4字节 ， 要比bigint8字节少一半 。 这也是为什么b+树要求把真实的数据放到叶子节点而不是内层节点 ， 一旦放到内层节点 ， 磁盘块的数据项会大幅度下降 ， 导致树增高 。 当数据项等于1时将会退化成线性表 。
2. 当b+树的数据项是复合的数据结构 ， 比如(name,age,sex)的时候 ， b+数是按照从左到右的顺序来建立搜索树的 ， 比如当(张三,20,F)这样的数据来检索的时候 ， b+树会优先比较name来确定下一步的所搜方向 ， 如果name相同再依次比较age和sex ， 最后得到检索的数据；但当(20,F)这样的没有name的数据来的时候 ， b+树就不知道下一步该查哪个节点 ， 因为建立搜索树的时候name就是第一个比较因子 ， 必须要先根据name来搜索才能知道下一步去哪里查询 。 比如当(张三,F)这样的数据来检索时 ， b+树可以用name来指定搜索方向 ， 但下一个字段age的缺失 ， 所以只能把名字等于张三的数据都找到 ， 然后再匹配性别是F的数据了 ，这个是非常重要的性质 ， 即索引的最左匹配特性 。
   • 上一页
   • 1
   • 2
   • 3
   • 4
   • 5
   • 6
   • 下一页
   
   

   
   

   • 三星|顶配旗舰重回最低价，三个月降价四百，12G+256G+120W
   • 路由器|千兆双频WiFi6，还能异地组网，什么神仙路由器只卖三百多？
   • 电池|百元级散热器，超频三东海R4000拯救热到可以蒸蛋的机箱
   • 荣耀|建议收藏！2021年底盘点：这三款旗舰可以让你安逸地使用两三年
   • 酷派|酷派：国产手机“假高端”严重，用户不应分为三六九等
   • 苹果|要是不看真实数据，我还以为国产机将iPhone打成下一个三星了呢
   • 电池|2021年年底买千元机，这四款用三五年没问题，十二月购机必看
   • wi-fi6|12月物超所值的三款高性价比手机推荐 价格不超过3000元
   • iphone13|iPhone13 缺货问题得到改善，发货时间变快，第三方优惠将更大
   • realme|买不起“十三香”？目前这4款真香机最值得买，三五年不卡顿