生活_傻大方

  1. 首页 > 潮·科技 > >

技术干货（四）「LeetCode」51 - 60题详解

51. N 皇后n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上 ， 并且使皇后彼此之间不能相互攻击 。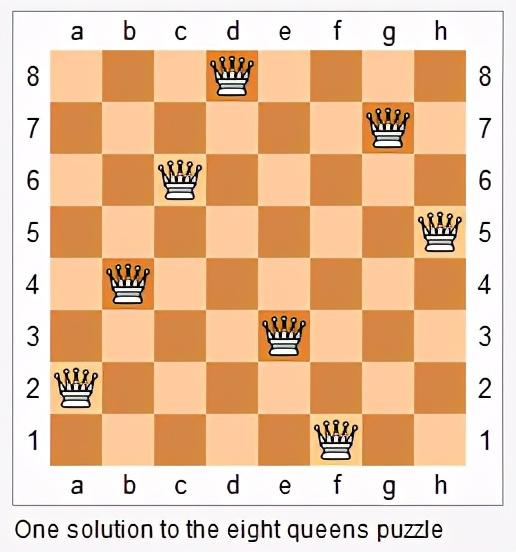
技术干货（四）「LeetCode」51 - 60题详解文章插图
上图为 8 皇后问题的一种解法 。
给定一个整数 n ， 返回所有不同的 n 皇后问题的解决方案 。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案 ， 该方案中 'Q' 和 '.' 分别代表了皇后和空位 。
示例：
输入：4输出：[ [".Q..",// 解法 1"...Q","Q...","..Q."], ["..Q.",// 解法 2"Q...","...Q",".Q.."]]解释: 4 皇后问题存在两个不同的解法 。 提示：

  • 皇后彼此不能相互攻击 ， 也就是说：任何两个皇后都不能处于同一条横行、纵行或斜线上 。
class Solution {List res = new ArrayList<>();public List solveNQueens(int n) {char[][] board = new char[n][n];// 初始化boardfor(char[] chs : board) Arrays.fill(chs, '.');// 从第一行开始dfs(board, 0);return res;}void dfs(char[][] board, int row){if(row == board.length){List result = new LinkedList<>();for(char[] r: board) result.add(String.valueOf(r));res.add(result);return;}int n = board[0].length;// 尝试遍历一行的位置放上Qfor(int col = 0; col < n; col ++){// 排除无效情况if(!valid(board, row , col)) continue;// 尝试放皇后board[row][col] = 'Q';dfs(board, row + 1);// 重置board[row][col] = '.';}}boolean valid(char[][] board, int row , int col){int rows = board.length;// 判断列for (char[] chars : board) if (chars[col] == 'Q') return false;// 判断右对角for (int i = row - 1, j = col + 1; i >= 0i--, j++) {if (board[i][j] == 'Q') return false;}// 判断左对角for (int i = row - 1, j = col - 1; i >= 0i--, j--) {if (board[i][j] == 'Q') return false;}return true;}}52. N皇后 IIn 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上 ， 并且使皇后彼此之间不能相互攻击 。
技术干货（四）「LeetCode」51 - 60题详解文章插图
上图为 8 皇后问题的一种解法 。
给定一个整数 n ， 返回 n 皇后不同的解决方案的数量 。
示例:
输入: 4输出: 2解释: 4 皇后问题存在如下两个不同的解法 。 [ [".Q..",// 解法 1"...Q","Q...","..Q."], ["..Q.",// 解法 2"Q...","...Q",".Q.."]]class Solution {int res = 0;public int totalNQueens(int n) {char[][] board = new char[n][n];// 初始化boardfor(char[] chs : board) Arrays.fill(chs, '.');// 从第一行开始dfs(board, 0);return res;}void dfs(char[][] board, int row){if(row == board.length){res ++;return;}int n = board[0].length;// 尝试遍历一行的位置放上Qfor(int col = 0; col < n; col ++){// 排除无效情况if(!valid(board, row , col)) continue;// 尝试放皇后board[row][col] = 'Q';dfs(board, row + 1);// 重置board[row][col] = '.';}}boolean valid(char[][] board, int row , int col){int rows = board.length;// 判断列for (char[] chars : board) if (chars[col] == 'Q') return false;// 判断右对角for (int i = row - 1, j = col + 1; i >= 0i--, j++) {if (board[i][j] == 'Q') return false;}// 判断左对角for (int i = row - 1, j = col - 1; i >= 0i--, j--) {if (board[i][j] == 'Q') return false;}return true;}}53. 最大子序和给定一个整数数组 nums， 找到一个具有最大和的连续子数组（子数组最少包含一个元素） ， 返回其最大和 。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]输出: 6解释: 连续子数组 [4,-1,2,1] 的和最大 ， 为 6 。 进阶:
如果你已经实现复杂度为 O(n) 的解法 ， 尝试使用更为精妙的分治法求解 。
public int maxSubArray(int[] nums) {int res = Integer.MIN_VALUE, prev = 0;for(int i = 0; i < nums.length; i++){int now = Math.max(prev, 0) + nums[i];res = Math.max(now, res);prev = now;}return res;}54. 螺旋矩阵给定一个包含 m x n 个元素的矩阵（m 行, n 列） ， 请按照顺时针螺旋顺序 ， 返回矩阵中的所有元素 。
示例 1:
输入:[ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ]]输出: [1,2,3,6,9,8,7,4,5]示例 2:
输入:[[1, 2, 3, 4],[5, 6, 7, 8],[9,10,11,12]]输出: [1,2,3,4,8,12,11,10,9,5,6,7]解法一public List spiralOrder(int[][] matrix) {List res = new ArrayList<>();if(matrix == null || matrix.length == 0) return res;int n = matrix.length, m = matrix[0].length;boolean[][] st = new boolean[n][m];int[] dx = {0, 1, 0, -1};int[] dy = {1, 0, -1, 0};int x = 0, y = 0, d = 0;for(int i = 0;i < m * n; i ++){res.add(matrix[x][y]);st[x][y] = true;int a = x + dx[d], b = y + dy[d];// 转向的条件 1. 越界 2. 走过if( a < 0 || b < 0|| a>= n || b >= m || st[a][b]) {d = (d + 1) % 4;a = x + dx[d]; b = y + dy[d];}// 更新下一个点的位置x = a; y = b;}return res;}



上一篇：并发控制工具相位器Phaser实现原理

下一篇：激光电视带动大屏市场，优势非常明显，但唯一缺点不能忽视