支持向量机超参数的可视化解释支持向量机（SVM）是一种应用

文章插图
支持向量机（SVM）是一种应用广泛的有监督机器学习算法。它主要用于分类任务，但也适用于回归任务。
在这篇文章中，我们将深入探讨支持向量机的两个重要超参数C和gamma ，并通过可视化解释它们的影响。所以我假设你对算法有一个基本的理解，并把重点放在这些超参数上。
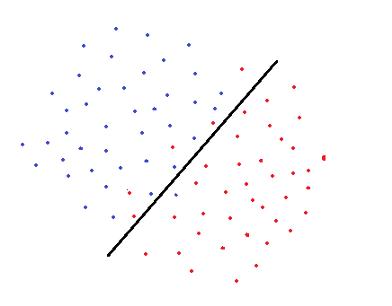
支持向量机用一个决策边界来分离属于不同类别的数据点。在确定决策边界时，软间隔支持向量机（soft margin是指允许某些数据点被错误分类）试图解决一个优化问题，目标如下：

增加决策边界到类（或支持向量）的距离
使训练集中正确分类的点数最大化

文章插图
显然，这两个目标之间有一个折衷，它是由C控制的，它为每一个错误分类的数据点增加一个惩罚。
如果C很小，对误分类点的惩罚很低，因此选择一个具有较大间隔的决策边界是以牺牲更多的错误分类为代价的。
当C值较大时，支持向量机会尽量减少误分类样本的数量，因为惩罚会导致决策边界具有较小的间隔。对于所有错误分类的例子，惩罚是不一样的。它与到决策边界的距离成正比。
在这些例子之后会更加清楚。让我们首先导入库并创建一个合成数据集。

import numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.svm import SVCfrom sklearn.datasets import make_classificationX, y = make_classification(n_samples=200, n_features=2,n_informative=2, n_redundant=0, n_repeated=0, n_classes=2,random_state=42)plt.figure(figsize=(10,6))plt.title("Synthetic Binary Classification Dataset", fontsize=18)plt.scatter(X[:,0], X[:,1], c=y, cmap='cool')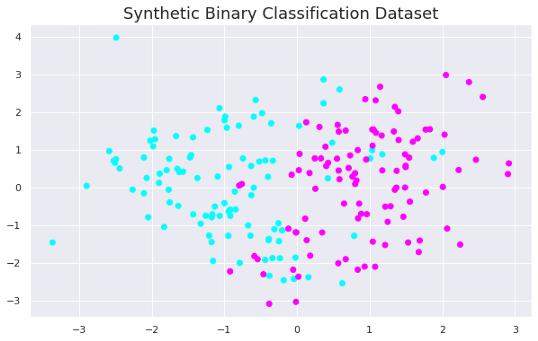

文章插图
我们先训练一个只需调整C的线性支持向量机，然后实现一个RBF核的支持向量机，同时调整gamma参数。
我们现在可以创建两个不同C值的线性SVM分类器。

clf = SVC(C=0.1, kernel='linear').fit(X, y)plt.figure(figsize=(10,6))plt.title("Linear kernel with C=0.1", fontsize=18)plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='cool')plot_svc_decision_function(clf)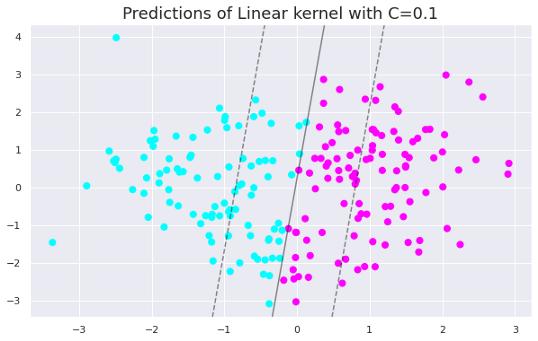

文章插图
只需将C值更改为100即可生成以下绘图。

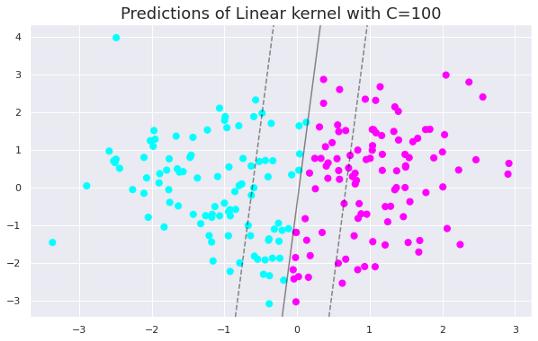文章插图
当我们增加C值时，间隔会变小。因此，低C值的模型更具普遍性。随着数据集的增大，这种差异变得更加明显。
线性核的超参数只达到一定程度上的影响。在非线性内核中，超参数的影响更加明显。
Gamma是用于非线性支持向量机的超参数。最常用的非线性核函数之一是径向基函数（RBF）。 RBF的Gamma参数控制单个训练点的影响距离。
gamma值较低表示相似半径较大，这会导致将更多的点组合在一起。对于gamma值较高的情况，点之间必须非常接近，才能将其视为同一组（或类）。因此，具有非常大gamma值的模型往往过拟合。
让我们绘制三个不同gamma值的支持向量机的预测图。

clf = SVC(C=1, kernel='rbf', gamma=0.01).fit(X, y)y_pred = clf.predict(X)plt.figure(figsize=(10,6))plt.title("Predictions of RBF kernel with C=1 and Gamma=0.01", fontsize=18)plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='cool')plot_svc_decision_function(clf)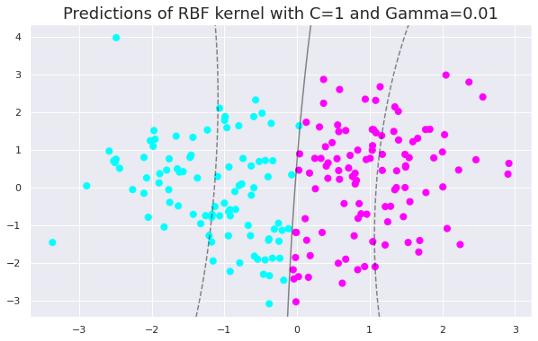

文章插图
只需更改gamma值即可生成以下绘图。

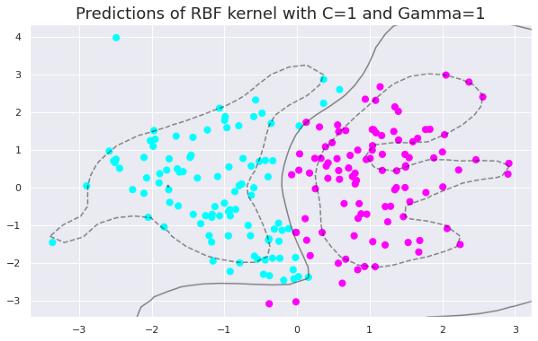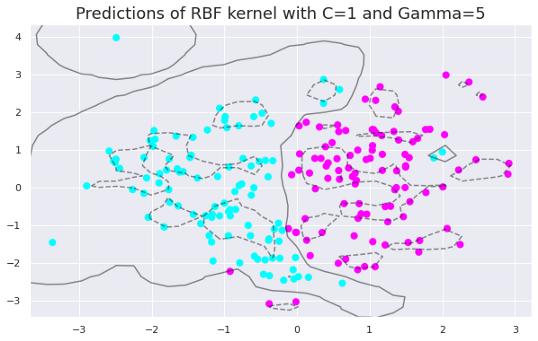文章插图

文章插图
随着gamma值的增加，模型变得过拟合。数据点需要非常接近才能组合在一起，因为相似半径随着gamma值的增加而减小。
在gamma值为0.01、1和5时， RBF核函数的精度分别为0.89、0.92和0.93 。这些值表明随着gamma值的增加，模型对训练集的拟合度逐渐增加。
gamma与C参数对于线性核，我们只需要优化c参数。然而，如果要使用RBF核函数，则c参数和gamma参数都需要同时优化。如果gamma很大， c的影响可以忽略不计。如果gamma很小， c对模型的影响就像它对线性模型的影响一样。 c和gamma的典型值如下。但是，根据具体应用，可能存在特定的最佳值：