BGLL社团划分|DBSCAN密度聚类|Python复杂网络
BGLL社团划分案例分析具有复杂相互作用的大量个体系统 , 复杂网络是常用的工具 。 大多数复杂网络呈现社团结构 , 即节点组织成紧密相连的群组 , 在同一个群组内的节点连接相对紧密 , 而不同群组间的节点连接相对稀疏 。 一个群组通常对应着一个功能单元 , 例如代谢网同一群组内的代谢物可能实现的是同一功能 。 因此复杂网络的社团划分可以大大简化复杂系统的功能分析 , 在药物功能分析、商品推荐、网络导航、万维网结构设计等有广泛应用 。
数据描述:
network.txt为无向网络 , 没有自边或者重边,网络节点数115 , 节点从1开始编号 。 每一行为一个二元组 , 二元组的两个数表示两个节点间有无向边相连 。
问题:
请将该网络划分为你认为合适的社团数目 。
提交结果:
请在正文(结果汇总.pdf)中详细描述解答过程 , 包括解题思路 , 算法 , 及分析划分的结果 , 并提交以下2个附录文件:
1. 代码;
2. 网络的划分结果,用Community_Detection.csv命名 , 格式如下:
(节点1 所属社团编号i)
(节点2 所属社团编号j)
社团编号从1开始
数据如下: 文章插图
文章插图
社团划分
1. 社团划分预备知识
一个图通常表示为G=(V,E) , 其中V表示点集合 , E表示边集合 , 通常我们用n表示图的节点数 , m表示边数 。 一个图中 , 与一个点的相关联的边的数量称为该点的度 。 对于一个图 , 图中所有点的度的和恰好等于边数的两倍 。 图通常用邻接矩阵A表示 , 邻接矩阵的(i,j)位置元素是1表示点i到点j右边 , 0表示无边 。本文中我们会用到随机图的概念 , 所谓随机图 , 就是指一个图中任何两个点之间连边的概率相等 。 首先确定n个点 , 然后以固定概率p去给图中的一对顶点连边 , 就形成了一个随机图 。 在研究中,随机图通常用来作为一个空模型来与实际网络进行比较 , 从而得出一些性质结论 。研究社团的划分 , 一个需要解决的问题是 , 如何来衡量一个社团的划分的好坏?一个比较简单直观的原则是使得社区内部的边尽可能地多 , 社区之间的边间可能地少 。 另外一个稍微复杂点但是更为常用的度量是Newman等人提出的模块度(modularity)的概念 , 基本的想法是这样的:我们假设在随机图中是不存在这种社团结构的 , 将实际网络跟其相应的随机网络进行比较 , 如果一个网络跟随机网络之间的差异越大 , 表示社团结构越明显 。 这样 , 我们对划分后的每一个子网络计算一个“密度” , 然后计算该子网络随机情况下的“密度” , 这两个“密度”存在一个差值 , 表示了该子网络偏离随机情况的一种程度 , 并且这个值越大表示这个子网络相对随机网络越稠密 。 一个网络中包含的所有子网络的这个差值加到一起的和就是这个复杂网络的模块度 , 数学公式表示如下: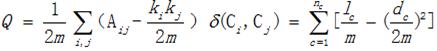 文章插图
文章插图
其中Aij表示图的邻接矩阵 , ki 表示点i 的度 , m是图的边数 , ki*kj/2m表示点 i 和点 j之间边的期望 。 进一步将模块度可以化为等式右边的形式 , nc是社团的总个数 , lc是社团c内的边数 , dc是社团内的点的度数之和 (note: 社团内的每一个点可能跟本社团内部的点有边 , 也可能有跟其他社团点连边 , 故通常 dc> lc)
2. BGLL算法
BGLL算法就属于基于模块度优化中的聚合类算法 , 自底向上的不断聚合 。
BGLL算法主要分为两步:
第一步:假设网络中有N个节点 , 首先我们给每个节点分配一个社区 , 所以初始阶段有多少个节点就有多少个社区 。 然后 , 对于网络中每个节点i,我们考虑他所有的邻居节点j,我们评估当把节点i从它所在的社区移动到其邻居j所在的社区时 , 模块度的增量变化 , 我们把节点i移动到使模块度增加最大的节点j所在的社区 。 如果所有计算出来的增益都不是正数 , 则将该节点仍处于原社区中 。 该过程对所有的节点重复并且按顺序应用 , 直到没有节点移动 , 则第一个过程停止 , 也就是任何一个节点的移动都不会导致模块度的增加 。 从该过程可以肯定 , 有些节点会被不止一次的考虑到 。 当然节点考虑顺序对算法最后的输出也是有影响的 , 但是最后对最后所划分的社区的模块度影响不大 。 但是节点的排序顺序是可以影响算法的运行时间的 。
每一次节点移动一个孤立节点到其邻居所在的社团模块度增益为ΔQ: 文章插图
文章插图
- 级别|自动驾驶级别如何划分?
- 了解情绪划分:如何使用机器学习来保持积极心态?
- 天猫|天猫入驻:天猫现在可以入驻吗?猫店侠划分重点
- AI|YouTube 利用 AI 来为视频划分章节
- AI|YouTube正测试通过AI帮创作者划分视频章节
- VLAN的划分和网络的配置实例
- Java的内存区域划分
- 2020年中国5G产业建设现状与建设规划分析
- 文峥解说|阴阳师:发动战争的大岳丸不该被同情?玩个游戏何必要划分阵营!
- 水晶先锋|英雄联盟:明明技能如此厉害,为何他们常年被划分为冷门英雄?
