非典型算法题，用程序和电脑玩一个游戏大家好

大家好，欢迎阅读周末算法题专题。
今天选择的算法题是来自contest 1407比赛的C题，这题全场通过6700余人。通过的人数虽然多，但是这题真的不简单，想出算法来不太容易。抛开难度不提，这道题非常非常有意思，老实说这种形式的题目我也是第一次见。
题目链接：
废话不多说，我们来看题目。
题意这题是一道非典型的算法题，与其说是一道算法题不如说更像是一个游戏。游戏的目的是猜一个1至n这n个数构成的排列，我们需要通过输入和输出和系统进行交互，从系统处获取更多的信息，最终给出猜测的结果。
首先系统会给定一个整数n ，表示这个排列由n个数字构成，这n个数字由前n个正整数构成，也就是1到n这n个数字。之后我们可以通过输出一个命令的形式向系统进行提问，提问的方式是? x y 。系统会计算排列当中第x个数对第y个数取模的结果进行返回（排列的下标从1开始），也就是返回
num[x] % num[y] 的值。
系统最多接受2n次询问，当我们已经猜出整个排列之后，输出这个排列。其中n <= 1e4 。
样例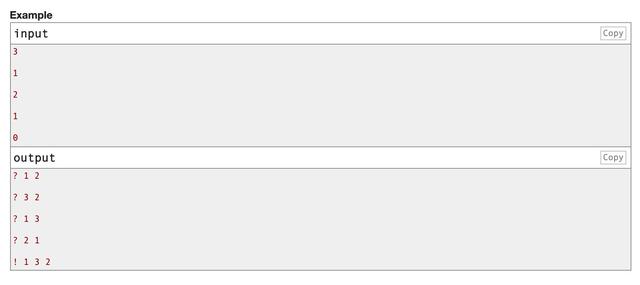
文章插图
这个样例要倒过来看，第一个输入的3表示n 。接着就先看输出再看输入。这个样例要猜的结果是[1, 3, 2] ，首先询问了num[1]对num[2]取余的结果，系统返回是1 。接着询问num[3]对num[2]取余的结果，答案是2 。接着询问num[1]%num[3]和num[2]%num[1] ，得到的结果分别是1和0 。最终我们根据这些信息猜测出了这个排列是[1, 3, 2] ，通过! 1 3 2的形式进行返回。
思路那道题之后我们首先可以发现， n确定了之后这n个数也就确定了。因为n最大，其他数对n取模都是它本身。所以我们需要先找到n的位置。
但是n的位置并不好找，想来想去只有一种办法，就是当出现两个数的余数是n-1的时候，就可以确定这两个数一个是n-1另外一个是n 。但是很明显，这样做我们无法在规定步数内解出来。因为n个数两两组合一共有接近n^2种，但是题目限定我们最多只能询问2n次。
很显然，先找到n再寻找其他值是不行的。
【非典型算法题，用程序和电脑玩一个游戏】既然这个想法不行，我又开始找起了其他方法。我们求了x % y的结果之后，究竟有什么用呢？这个结果到底有没有其他信息呢？
我们来简单分析一下，我们假设x % y = 1 ，那么这能说明什么吗？很明显，不能说明什么，因为可能性太多了。 1对其他数取模都等于1 ， x % (x-1)也等于1 。但假如x % y > (n/2) 呢？其实就能说明问题了。因为x和y的范围是[1, n] ，现在两个数取模之后的结果大于n的一半，很明显说明x就是这个结果， y是比x更大的数。还有一种情况是x % y = 0 ，这种情况我们虽然无法确定x和y的值，但是可以知道x一定是y的倍数且x > y 。
虽然知道这些，但还是不够解开问题，仍然需要碰运气，因为我们并不能保证在查询次数内刚好就可以找到所有比二分之n大的数。但是这一段分析并不是无用的，我们可以在此基础上更进一步。我们求了x和y的余数之后可以再求一下y和x的余数，假设x % y = a, y % x = b ，通过分析a和b我们能够得到什么结果呢？
首先我们可以肯定a和b不会相等，原因也很简单，因为x和y一定不等（排列中的数各不相同）。我们不妨假设x > y ，那么y % x =b = y ， x % y = a < y 。如果a和b相等的话，那么就有 y < y ，这显然是不成立的。所以可以肯定a和b一定不等。其次从上面的证明我们也看得出来，在x > y时，那么一定可以得到a < b 。因为a = x % y < y ， b = y % x = y 。也就是说我们可以通过a和b的关系判断x和y的关系，不仅如此，还可以确定y的值。
到这里距离解出这道题已经非常接近了，只差临门一脚，但是这里我还是走了弯路。我当时的想法是把这些数两两配对，这样就可以确定出其中的一半。之后我们再把解不出来的数再进行配对，直到最后只剩下一个数为止。后来发现也有反例，比如[1, 3, 2, 4, 5] ，在这个例子当中1和3配对， 2和4配对， 5落单。我们还是没办法解出来。
我在这里苦思冥想了很久，后来才发现答案远在天边近在眼前，解法其实非常简单。我们只需要从前往后遍历维护一个最大值即可。我们假设最大值是id ，凡是遇到小于id的数，都可以通过它和id取模的结果求出来。如果遇到了比id更大的数，同样可以通过取模的结果求出id 。所以到最后的时候，我们可以求出除了最大值其他的所有数，这个剩下的数就是n 。