堆的存储一般都用数组来存储堆 ， i节点的父节点下标就为( i – 1 ) / 2 (i – 1) / 2(i–1)/2 。 它的左右子节点下标分别为 2 ? i + 1 2 * i + 12?i+1 和 2 ? i + 2 2 * i + 22?i+2 。 如第0个节点左右子节点下标分别为1和2 。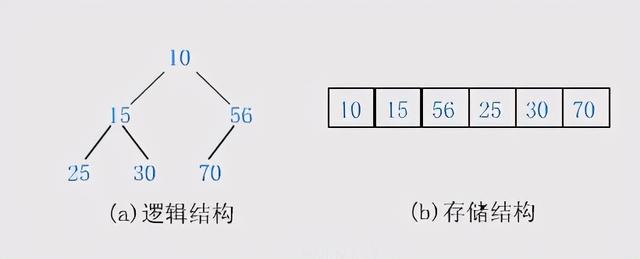
文章插图
2.2.2 堆的基本操作（1）建立以最小堆为例 ， 如果以数组存储元素时 ， 一个数组具有对应的树表示形式 ， 但树并不满足堆的条件 ， 需要重新排列元素 ， 可以建立“堆化”的树 。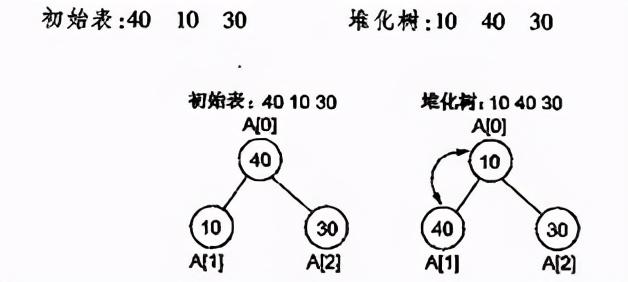
文章插图
（2）插入将一个新元素插入到表尾 ， 即数组末尾时 ， 如果新构成的二叉树不满足堆的性质 ， 需要重新排列元素 ， 下图演示了插入15时 ， 堆的调整 。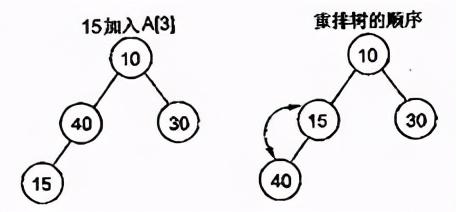
文章插图
（3）删除 。 堆排序中 ， 删除一个元素总是发生在堆顶 ， 因为堆顶的元素是最小的（小顶堆中） 。 表中最后一个元素用来填补空缺位置 ， 结果树被更新以满足堆条件 。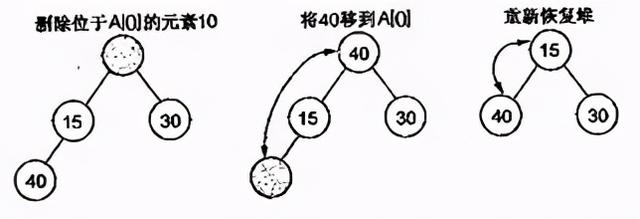
文章插图
2.2.3 堆操作实现（1）插入代码实现每次插入都是将新数据放在数组最后 。 可以发现从这个新数据的父节点到根节点必然为一个有序的数列 ， 现在的任务是将这个新数据插入到这个有序数据中 ， 这就类似于直接插入排序中将一个数据并入到有序区间中 ， 这是节点“上浮”调整 。 不难写出插入一个新数据时堆的调整代码：
//新加入i节点,其父节点为(i-1)/2//参数：a：数组 ， i：新插入元素在数组中的下标void minHeapFixUp(int a[], int i) {int j, temp;temp = a[i];j = (i-1)/2;//父节点while (j >= 0a[i]=a[j];//把较大的子节点往下移动,替换它的子节点i = j;j = (i-1)/2;}a[i] = temp;}因此 ， 插入数据到最小堆时：
//在最小堆中加入新的数据data//a：数组 ， index：插入的下标 ， void minHeapAddNumber(int a[], int index, int data) {a[index] = data;minHeapFixUp(a, index);} （2）删除代码实现按照堆删除的说明 ， 堆中每次都只能删除第0个数据 。 为了便于重建堆 ， 实际的操作是将数组最后一个数据与根节点交换 ， 然后再从根节点开始进行一次从上向下的调整 。
调整时先在左右儿子节点中找最小的 ， 如果父节点不大于这个最小的子节点说明不需要调整了 ， 反之将最小的子节点换到父节点的位置 。 此时父节点实际上并不需要换到最小子节点的位置 ， 因为这不是父节点的最终位置 。 但逻辑上父节点替换了最小的子节点 ， 然后再考虑父节点对后面的节点的影响 。 堆元素的删除导致的堆调整 ， 其整个过程就是将根节点进行“下沉”处理 。 下面给出代码：
//a为数组 ， len为节点总数；从index节点开始调整 ， index从0开始计算index其子节点为 2*index+1, 2*index+2；len/2-1为最后一个非叶子节点 void minHeapFixDown(int a[],int len,int index) { if(index>(len/2-1))//index为叶子节点不用调整return; int tmp=a[index]; lastIndex=index; while(index<=len/2-1)//当下沉到叶子节点时 ， 就不用调整了 {// 如果左子节点小于待调整节点if(a[2*index+1]根据堆删除的下沉思想 ， 可以有不同版本的代码实现 ， 以上是和孙凛同学一起讨论出的一个版本 ， 在这里感谢他的参与 ， 读者可另行给出 。 个人体会 ， 这里建议大家根据对堆调整过程的理解 ， 写出自己的代码 ， 切勿看示例代码去理解算法 ， 而是理解算法思想写出代码 ， 否则很快就会忘记 。
（3）建堆有了堆的插入和删除后 ， 再考虑下如何对一个数据进行堆化操作 。 要一个一个的从数组中取出数据来建立堆吧 ， 不用！先看一个数组 ， 如下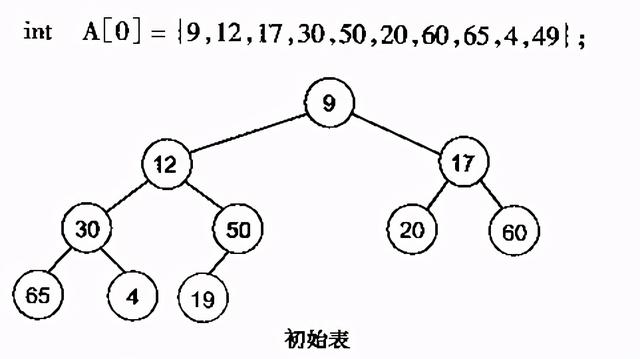图：
文章插图
很明显 ， 对叶子节点来说 ， 可以认为它已经是一个合法的堆了即20 ， 60 ，65 ，4 ，49都分别是一个合法的堆 。 只要从A[4]=50开始向下调整就可以了 。 然后再取A[3]=30 ， A[2] = 17 ， A[1] = 12 ， A[0] = 9分别作一次向下调整操作就可以了 。 下图展示了这些步骤：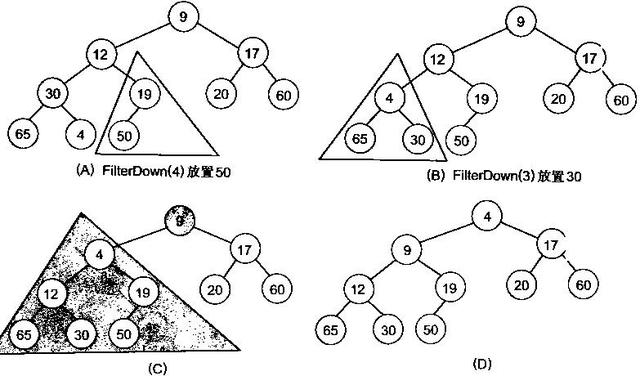
文章插图
写出堆化数组的代码：
//建立最小堆//a:数组 ， n：数组长度void makeMinHeap(int a[], int n) {for (int i = n/2-1; i >= 0; i--)minHeapFixDown(a, i, n);}2.2.4 堆的具体应用——堆排序堆排序（Heapsort）是堆的一个经典应用 ， 有了上面对堆的了解 ， 不难实现堆排序 。 由于堆也是用数组来存储的 ， 故对数组进行堆化后 ， 第一次将A[0]与A[n - 1]交换 ， 再对A[0…n-2]重新恢复堆 。 第二次将A[0]与A[n – 2]交换 ， 再对A[0…n - 3]重新恢复堆 ， 重复这样的操作直到A[0]与A[1]交换 。 由于每次都是将最小的数据并入到后面的有序区间 ， 故操作完成后整个数组就有序了 。 有点类似于直接选择排序 。