Nice！第一次见这么全面的Java实现八大排序算法，爱了( 五 ) 它们都属于内部排序

复杂度分析以下是快速排序算法复杂度:
文章插图
归并排序归并排序是建立在归并操作上的一种有效的排序算法， 1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。
基本思想归并排序算法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序的序列合并为整体有序序列。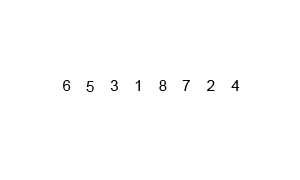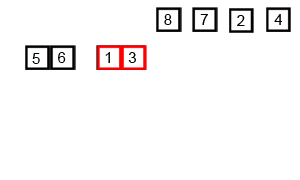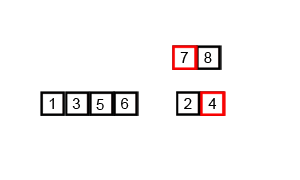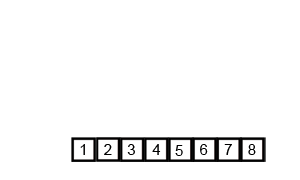
文章插图
算法描述归并排序可通过两种方式实现:

自上而下的递归
自下而上的迭代

递归法（假设序列共有n个元素）：

将序列每相邻两个数字进行归并操作，形成 floor(n/2)个序列，排序后每个序列包含两个元素；
将上述序列再次归并，形成 floor(n/4)个序列，每个序列包含四个元素；
重复步骤2 ，直到所有元素排序完毕。

文章插图
迭代法

申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
设定两个指针，最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾

代码实现归并排序其实要做两件事：

分解：将序列每次折半拆分
合并：将划分后的序列段两两排序合并

因此，归并排序实际上就是两个操作，拆分+合并
下面是递归的方法：

public class Merge {//归并所需的辅助数组private static int[] aux;public static void sort(int[] a) {//一次性分配空间aux = new int[a.length];sort(a, 0, a.length - 1);}public static void sort(int[] a, int low, int high) {if (low >= high) {return;}int mid = (low + high) / 2;//将左半边排序sort(a, low, mid);//将右半边排序sort(a, mid + 1, high);merge(a, low, mid, high);}/*** 该方法先将所有元素复制到aux[]中 ， 然后在归并会a[]中 。 方法咋归并时(第二个for循环)* 进行了4个条件判断：* - 左半边用尽(取右半边的元素)* - 右半边用尽(取左半边的元素)* - 右半边的当前元素小于左半边的当前元素(取右半边的元素)* - 右半边的当前元素大于等于左半边的当前元素(取左半边的元素)* @param a* @param low* @param mid* @param high*/public static void merge(int[] a, int low, int mid, int high) {//将a[low..mid]和a[mid+1..high]归并int i = low, j = mid + 1;for (int k = low; k <= high; k++) {aux[k] = a[k];}for (int k = low; k <= high; k++) {if (i > mid) {a[k] = aux[j++];} else if (j > high) {a[k] = aux[i++];} else if (aux[j] < aux[i]) {a[k] = aux[j++];} else {a[k] = aux[i++];}}}}

复杂度分析以下是归并排序算法复杂度:

文章插图
从效率上看，归并排序可算是排序算法中的”佼佼者”. 假设数组长度为n ，那么拆分数组共需logn ， , 又每步都是一个普通的合并子数组的过程，时间复杂度为O(n) ，故其综合时间复杂度为O(nlogn) 。另一方面，归并排序多次递归过程中拆分的子数组需要保存在内存空间，其空间复杂度为O(n) 。
总结与思考归并排序最吸引人的性质是它能够保证将任意长度为N的数组排序所需时间和NlogN成正比，它的主要缺点则是他所需的额外空间和N成正比。
基数排序基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机（Tabulation Machine）, 排序器每次只能看到一个列。它是基于元素值的每个位上的字符来排序的。对于数字而言就是分别基于个位，十位，百位或千位等等数字来排序。
基数排序（Radix sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。
基本思想它是这样实现的：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。