生活_傻大方

  1. 首页 > 潮·科技 > >

Nice！第一次见这么全面的Java实现八大排序算法，爱了

它们都属于内部排序 ， 也就是只考虑数据量较小仅需要使用内存的排序算法 ， 他们之间关系如下：
Nice！第一次见这么全面的Java实现八大排序算法，爱了文章插图
稳定与非稳定：
如果一个排序算法能够保留数组中重复元素的相对位置则可以被称为是 稳定 的 。 反之 ， 则是 非稳定 的 。
直接插入排序基本思想通常人们整理桥牌的方法是一张一张的来 ， 将每一张牌插入到其他已经有序的牌中的适当位置 。 在计算机的实现中 ， 为了要给插入的元素腾出空间 ， 我们需要将其余所有元素在插入之前都向右移动一位 。
算法描述一般来说 ， 插入排序都采用in-place在数组上实现 。 具体算法描述如下：

  1. 从第一个元素开始 ， 该元素可以认为已经被排序
  2. 取出下一个元素 ， 在已经排序的元素序列中从后向前扫描
  3. 如果该元素（已排序）大于新元素 ， 将该元素移到下一位置
  4. 重复步骤3 ， 直到找到已排序的元素小于或者等于新元素的位置
  5. 将新元素插入到该位置后
  6. 重复步骤2~5
动态效果如下：
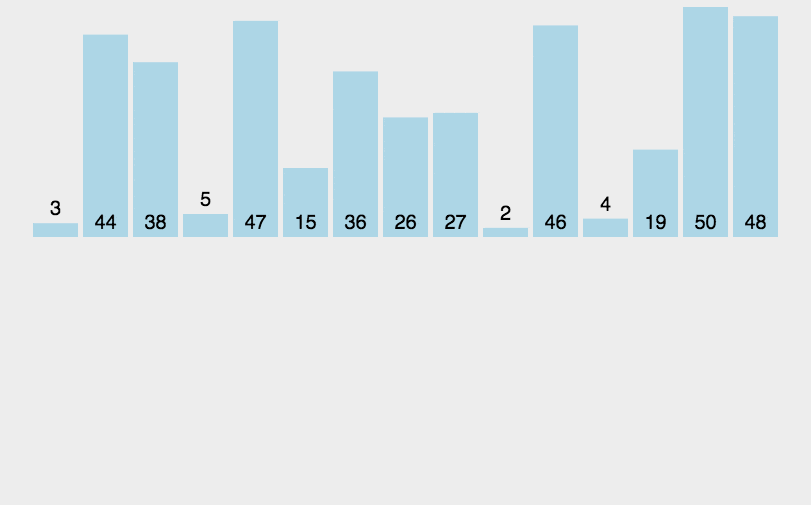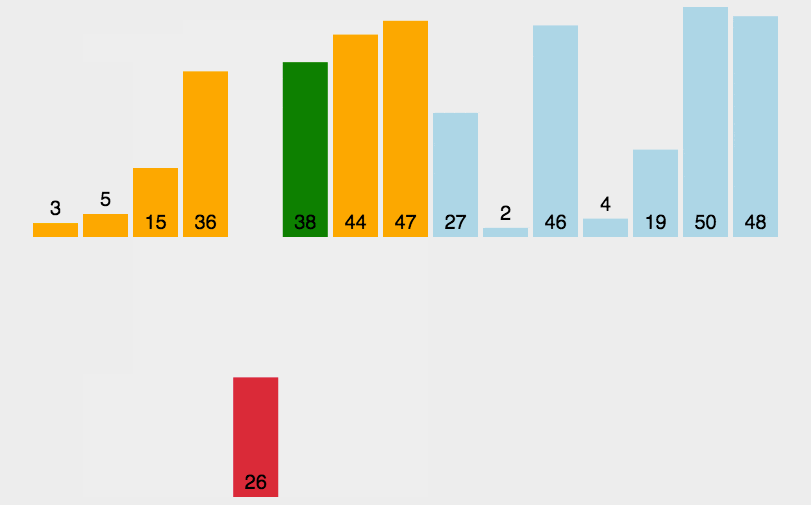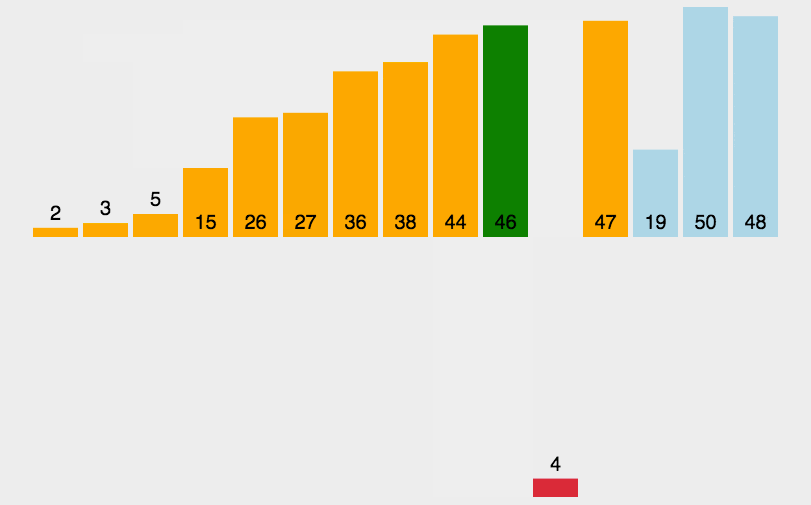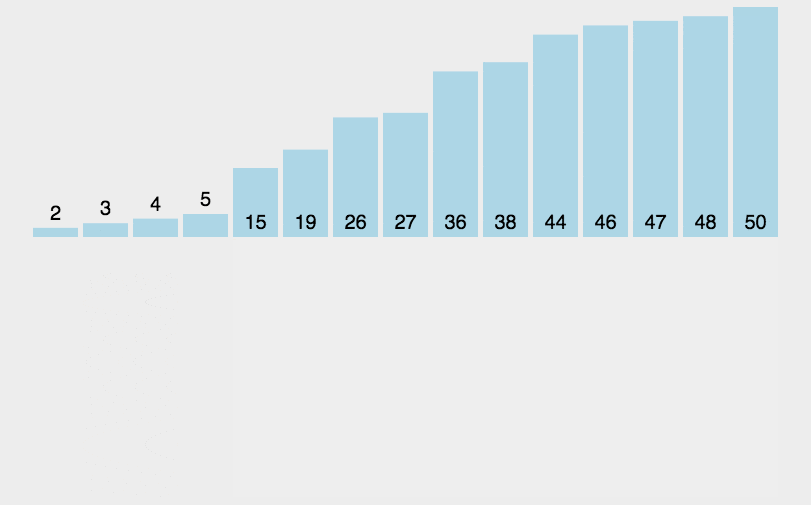Nice！第一次见这么全面的Java实现八大排序算法，爱了文章插图
注意：如果 比较操作 的代价比 交换操作 大的话 ， 可以采用二分查找法来减少 比较操作 的数目 。 该算法可以认为是 插入排序 的一个变种 ， 称为二分查找插入排序 。
代码实现/** * 通过交换进行插入排序 ， 借鉴冒泡排序 * * @param a */public static void sort(int[] a) {for (int i = 0; i < a.length - 1; i++) {for (int j = i + 1; j > 0; j--) {if (a[j] < a[j - 1]) {int temp = a[j];a[j] = a[j - 1];a[j - 1] = temp;}}}}/** * 通过将较大的元素都向右移动而不总是交换两个元素 * * @param a */public static void sort2(int[] a) {for (int i = 1; i < a.length; i++) {int num = a[i];int j;for (j = i; j > 0j--) {a[j] = a[j - 1];}a[j] = num;}}复杂度分析直接插入排序复杂度如下：
平均时间复杂度最好情况最坏情况空间复杂度O(n2)O(n2)O(n2)O(1)
比较与总结插入排序所需的时间取决于输入元素的初始顺序 。 例如 ， 对一个很大且其中的元素已经有序(或接近有序)的数组进行排序将会比随机顺序的数组或是逆序数组进行排序要快得多 。
希尔排序希尔排序 ， 也称 递减增量排序算法 ， 是插入排序的一种更高效的改进版本 。 希尔排序是 非稳定排序算法 。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
  • 插入排序在对几乎已经排好序的数据操作时 ， 效率高 ， 即可以达到线性排序的效率
  • 但插入排序一般来说是低效的 ， 因为插入排序每次只能将数据移动一
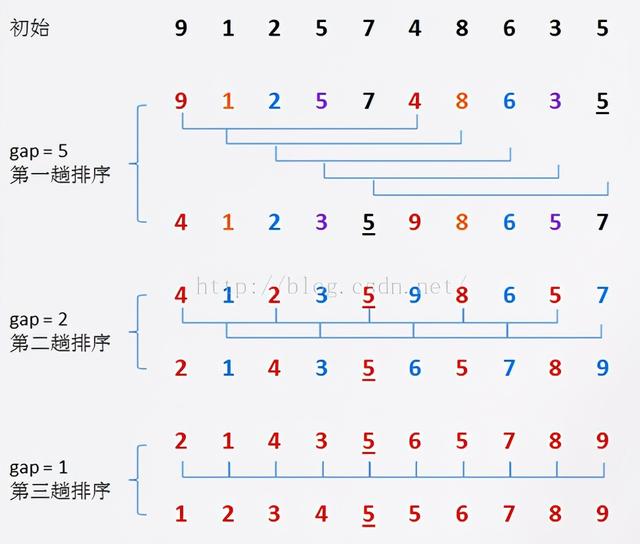
【Nice！第一次见这么全面的Java实现八大排序算法，爱了】希尔排序是先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序 ， 待整个序列中的记录“基本有序”时 ， 再对全体记录进行依次直接插入排序 。
基本思想将待排序数组按照步长gap进行分组 ， 然后将每组的元素利用直接插入排序的方法进行排序；每次再将gap折半减小 ， 循环上述操作；当gap=1时 ， 利用直接插入 ， 完成排序 。
可以看到步长的选择是希尔排序的重要部分 。 只要最终步长为1任何步长序列都可以工作 。 一般来说最简单的步长取值是初次取数组长度的一半为增量 ， 之后每次再减半 ， 直到增量为1 。 更好的步长序列取值可以参考维基百科 。
算法描述
  1. 选择一个增量序列 t1 ， t2 ， …… ， tk ， 其中 ti > tj, tk = 1；
  2. 按增量序列个数 k ， 对序列进行 k 趟排序；
  3. 每趟排序 ， 根据对应的增量 ti ， 将待排序列分割成若干长度为 m 的子序列 ， 分别对各子表进行直接插入排序 。 仅增量因子为 1 时 ， 整个序列作为一个表来处理 ， 表长度即为整个序列的长度 。
效果如下：
Nice！第一次见这么全面的Java实现八大排序算法，爱了文章插图
代码实现下面参考《算法》中给出的步长选择策略 ， 《算法》中给出的解释是
下面代码中递增序列的计算和使用都很简单 ， 和复杂递增序列的性能接近 。 当可以证明复杂的序列在最坏情况下的性能要好于我们所使用的递增序列 。 更加优秀的递增序列有待我们去发现 。
public static void sort(int[] a) {int length = a.length;int h = 1;while (h < length / 3) h = 3 * h + 1;for (; h >= 1; h /= 3) {for (int i = 0; i < a.length - h; i += h) {for (int j = i + h; j > 0; j -= h) {if (a[j]



上一篇：15个欧盟国家联合致信欧盟，反对5G就是反对欧盟发展

下一篇：iQOO 5 Pro智能手机拍摄体验报告「Soomal」