【PyTorch1.7发布，支持CUDA11分布式训练】通过以下四种方法得到评估函数：
第一步检查游戏是否还在继续 。
这个阶段的背后编码逻辑是：如果它在 checkmate 时返回 true ， 程序将会检查轮到哪方移动 。 如果当前轮到白方移动 ， 返回值为 - 9999 ， 即上次一定是黑方移动 ， 黑色获胜；否则返回值为 + 9999 ， 表示白色获胜 。 对于僵局或比赛材料不足 ， 返回值为 0 以表示平局 。
代码实现方式：
if board.is_checkmate():if board.turn:return -9999else:return 9999if board.is_stalemate():return 0if board.is_insufficient_material():return 0第二步 ， 计算总的棋子数 ， 并把棋子总数传递给 material 函数 。
wp = len(board.pieces(chess.PAWN, chess.WHITE))bp = len(board.pieces(chess.PAWN, chess.BLACK))wn = len(board.pieces(chess.KNIGHT, chess.WHITE))bn = len(board.pieces(chess.KNIGHT, chess.BLACK))wb = len(board.pieces(chess.BISHOP, chess.WHITE))bb = len(board.pieces(chess.BISHOP, chess.BLACK))wr = len(board.pieces(chess.ROOK, chess.WHITE))br = len(board.pieces(chess.ROOK, chess.BLACK))wq = len(board.pieces(chess.QUEEN, chess.WHITE))bq = len(board.pieces(chess.QUEEN, chess.BLACK))第三步 ， 计算得分 。 material 函数得分的计算方法是：用各种棋子的权重乘以该棋子黑白两方个数之差 ， 然后求这些结果之和 。 而每种棋子的得分计算方法是：该棋子在该游戏实例中所处位置的 piece-square 值的总和 。
material = 100 * (wp - bp) + 320 * (wn - bn) + 330 * (wb - bb) + 500 * (wr - br) + 900 * (wq - bq)pawnsq = sum([pawntable[i] for i in board.pieces(chess.PAWN, chess.WHITE)])pawnsq = pawnsq + sum([-pawntable[chess.square_mirror(i)]for i in board.pieces(chess.PAWN, chess.BLACK)])knightsq = sum([knightstable[i] for i in board.pieces(chess.KNIGHT, chess.WHITE)])knightsq = knightsq + sum([-knightstable[chess.square_mirror(i)]for i in board.pieces(chess.KNIGHT, chess.BLACK)])bishopsq = sum([bishopstable[i] for i in board.pieces(chess.BISHOP, chess.WHITE)])bishopsq = bishopsq + sum([-bishopstable[chess.square_mirror(i)]for i in board.pieces(chess.BISHOP, chess.BLACK)])rooksq = sum([rookstable[i] for i in board.pieces(chess.ROOK, chess.WHITE)])rooksq = rooksq + sum([-rookstable[chess.square_mirror(i)]for i in board.pieces(chess.ROOK, chess.BLACK)])queensq = sum([queenstable[i] for i in board.pieces(chess.QUEEN, chess.WHITE)])queensq = queensq + sum([-queenstable[chess.square_mirror(i)]for i in board.pieces(chess.QUEEN, chess.BLACK)])kingsq = sum([kingstable[i] for i in board.pieces(chess.KING, chess.WHITE)])kingsq = kingsq + sum([-kingstable[chess.square_mirror(i)]for i in board.pieces(chess.KING, chess.BLACK)])第四步 ， 计算评价函数 ， 此时将会返回白棋的 material 得分和各棋子单独得分之和 。
eval = material + pawnsq + knightsq + bishopsq + rooksq + queensq + kingsqif board.turn:return evalelse:return -eval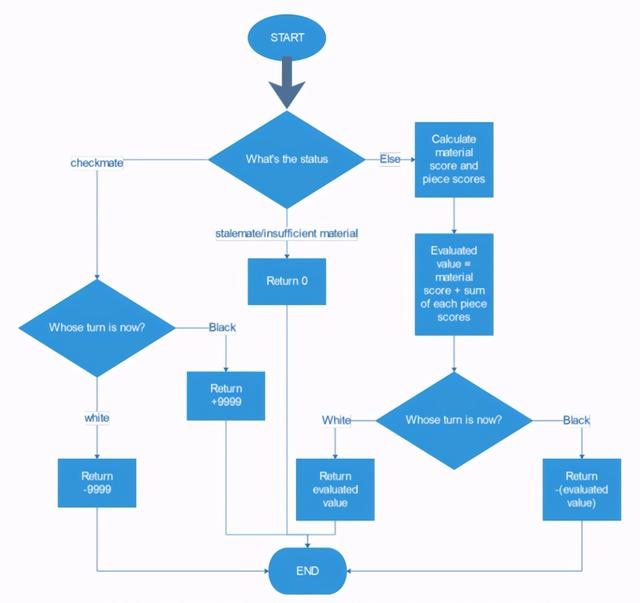
文章插图
评价函数流程图
移动选择
算法的最后一步是用 Minimax 算法中的 Negamax 实现进行移动选择 ， Minimax 算法是双人游戏（如跳棋等）中的常用算法 。 之后使用 Alpha-Beta 剪枝进行优化 ， 这样可以减少执行的时间 。
现在让我们深入研究一下 minimax 算法 。 该算法被广泛应用在棋类游戏中 ， 用来找出失败的最大可能性中的最小值 。 该算法广泛应用于人工智能、决策论、博弈论、统计和哲学 ， 力图在最坏的情况下将损失降到最低 。 简单来说 ， 在游戏的每一步 ， 假设玩家 A 试图最大化获胜几率 ， 而在下一步中 ， 玩家 B 试图最小化玩家 A 获胜的几率 。
为了更好地理解 minimax 算法 ， 请看下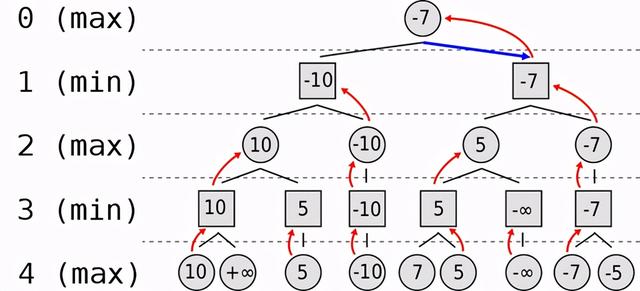图：
文章插图
维基百科中 minimax 树举例
为了得到更好的结果 ， 使用 minimax 变体 negamax ， 因为我们只需要一个最大化两位玩家效用的函数 。 不同点在于 ， 一个玩家的损失等于另一个玩家的收获 ， 反之亦然 。
就游戏而言 ， 给第一个玩家的位置值和给第二个玩家的位置值符号是相反的 。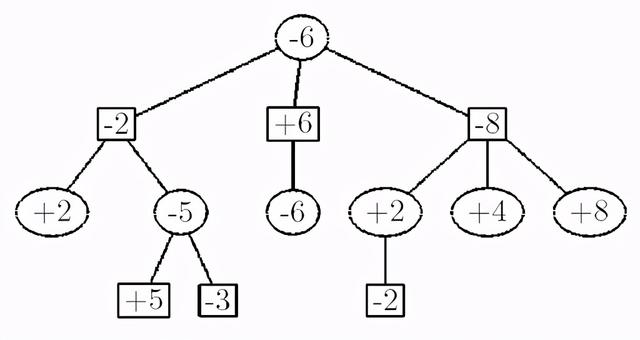
文章插图
negamax 示例
首先 ， 我们将 alpha 设为负无穷大 ， beta 设为正无穷大 ， 这样两位玩家都能以尽可能差的分数开始比赛 ， 代码如下：
except:bestMove = chess.Move.null()bestValue = http://kandian.youth.cn/index/-99999alpha = -100000beta = 100000for move in board.legal_moves:board.push(move)boardValue = -alphabeta(-beta, -alpha, depth - 1)if boardValue> bestValue:bestValue = http://kandian.youth.cn/index/boardValuebestMove = moveif (boardValue> alpha):alpha = boardValueboard.pop()return bestMove