动态规划算法——装最多水的容器来源:城北有个混子出处:动态规

【动态规划算法——装最多水的容器】来源:城北有个混子
出处:
动态规划概述动态规划（Dynamic Programming ， DP）是运筹学的一个分支，是求解决策过程最优化的过程。
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解，每一个解都对应于一个值，我们希望找到具有最优值的解。
动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案，不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中，这就是动态规划法的基本思路。
装最多水的容器给你 n 个非负整数 a1 ， a2 ， ... ， an ，每个数代表坐标中的一个点 (i, ai)。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) ，找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明：你不能倾斜容器，且 n 的值至少为 2 。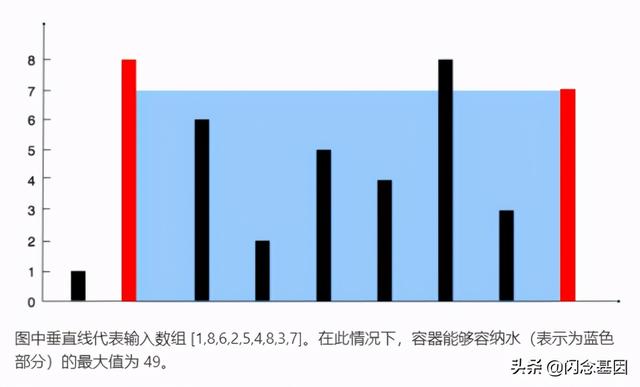
文章插图
示例：输入：[1,8,6,2,5,4,8,3,7]
输出：49
说明：当容器的两边分别是8和7的时候，容器所能盛水最多，最大储水面积为：7 *（9-2）= 49 。
问题分析本题是一道经典的面试题，最优的做法是使用「双指针」。一开始两个指针一个指向开头一个指向结尾，此时容器的底是最大的，接下来随着指针向内移动，会造成容器的底变小，在这种情况下想要让容器盛水变多，就只有在容器的高上下功夫。那我们该如何决策哪个指针移动呢？
我们能够发现不管是左指针向右移动一位，还是右指针向左移动一位，容器的底都是一样的，都比原来减少了 1 。这种情况下我们想要让指针移动后的容器面积增大，就要使移动后的容器的高尽量大，所以我们选择指针所指的高较小的那个指针进行移动，这样我们就保留了容器较高的那条边，放弃了较小的那条边，以获得有更高的边的机会。
这里用的就是动态规划，基本的表达式: areaMax = min(height[i], height[j]) * (j - i) 。
示例分析输入：[1,8,6,2,5,4,8,3,7]
输出：49
求解过程如下：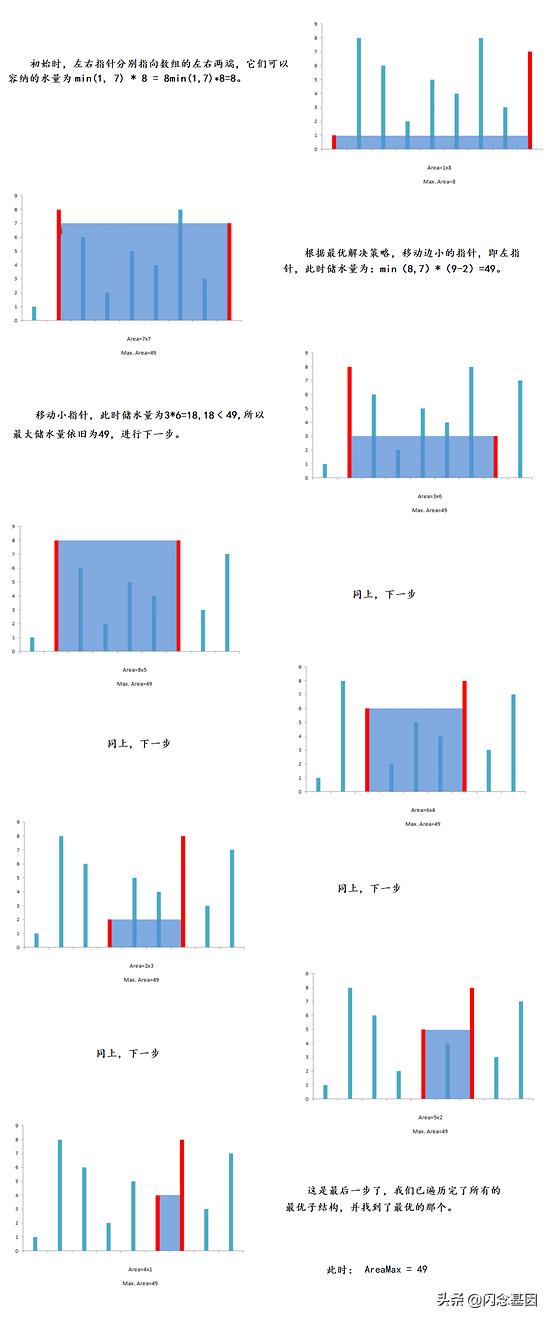
文章插图
算法实现public class TakeInWater {public static void main(String[] args) {int[] columns = {1,8,6,2,5,4,8,3,7};int areaMax = maxArea(columns);System.out.println("最大储水量：" + areaMax);}public static int maxArea(int[] height) {if (height.length < 1) {// 检验参数正确性return -1;}int left = 0;// 左指针int right = height.length-1;// 右指针int area = 0;// 最大储水量while (left < right) {int high = Math.min(height[left], height[right]);// 找到容器的储水高度area = Math.max(area, high*(right-left));// 最大储水量// 按照最优策略，移动指针if (height[left] < height[right]) {left++;}else {right--;}}return area;}}运行结果：
文章插图
来源:城北有个混子
出处: