1 说明
=====
1.1 欧拉数：就是自然常数 ， e 。
1.2 e是“指数”（exponential）的首字母 ， 也是欧拉名字的首字母 。
1.3 三大数学常数：自然常数e、圆周率π和虚数单位i 。
1.4 第一次把e看成常数的是雅各布?伯努利 ， 他开始尝试计算lim（1+1/n） n 的值；1727年欧拉首次用小写字母“e”表示这常数 。
文章插图
欧拉恒等式：真正的宇宙第一公式
文章插图
欧拉（Leonhard Euler ， 1707年4月15日－1783年9月18日） ， 瑞士数学家和物理学家
2 python实现自然常数e
==================
2.1 图1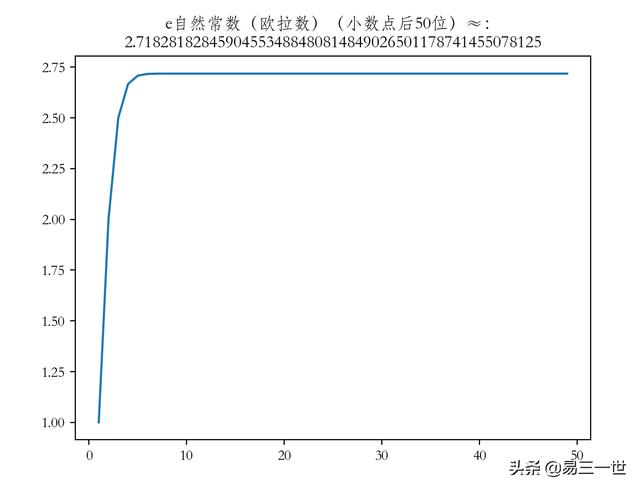
文章插图
图片1：静态
2.2 图2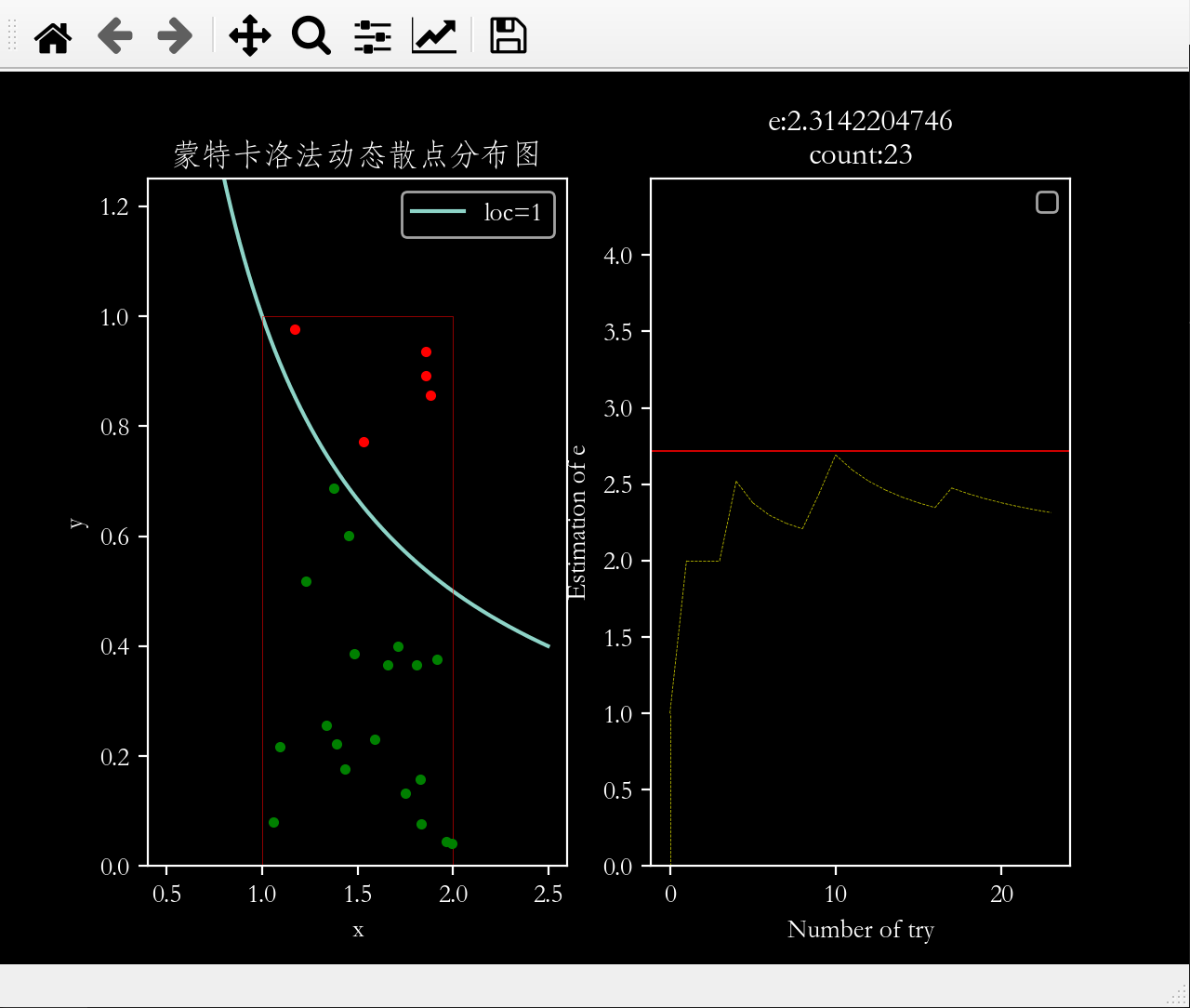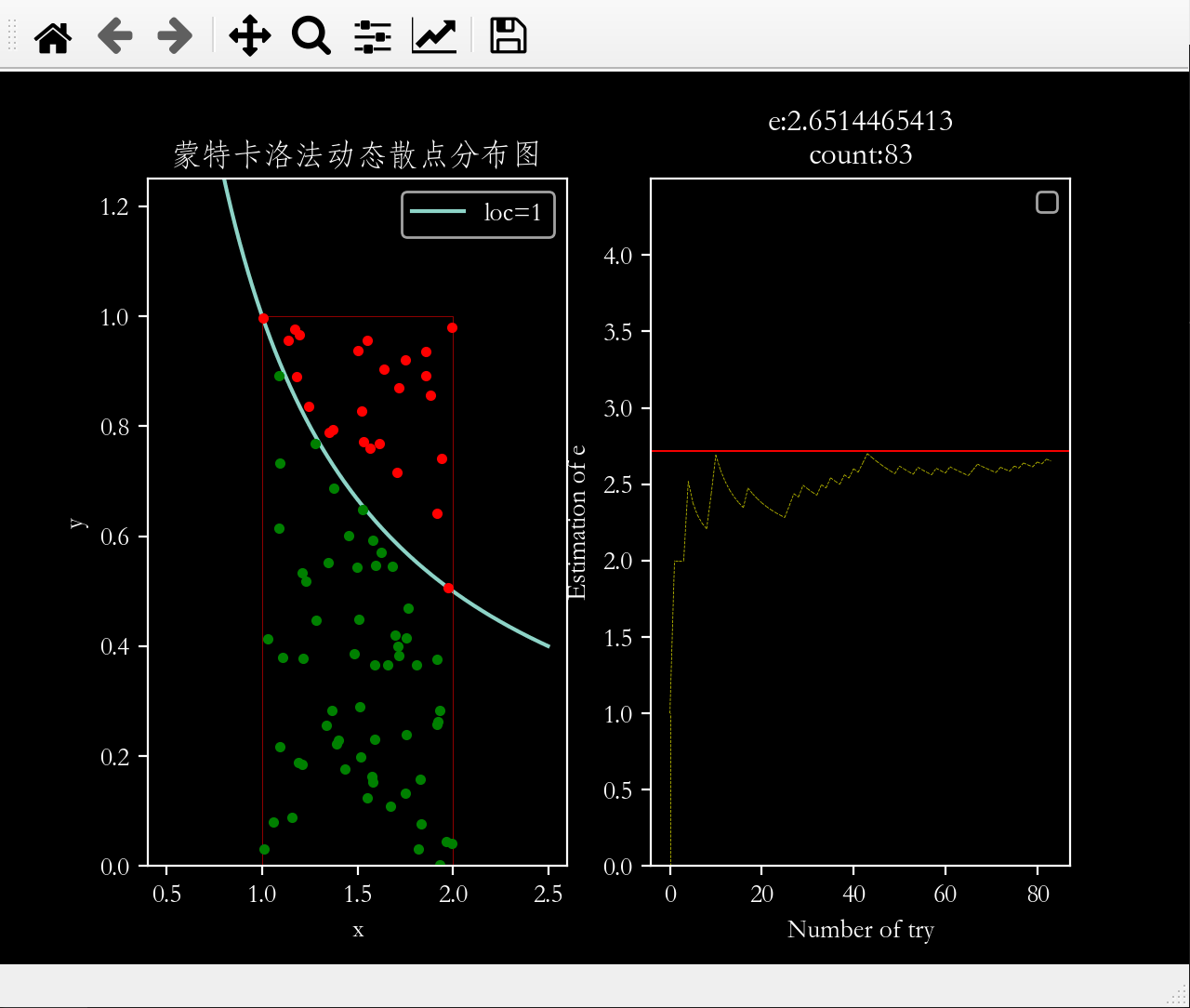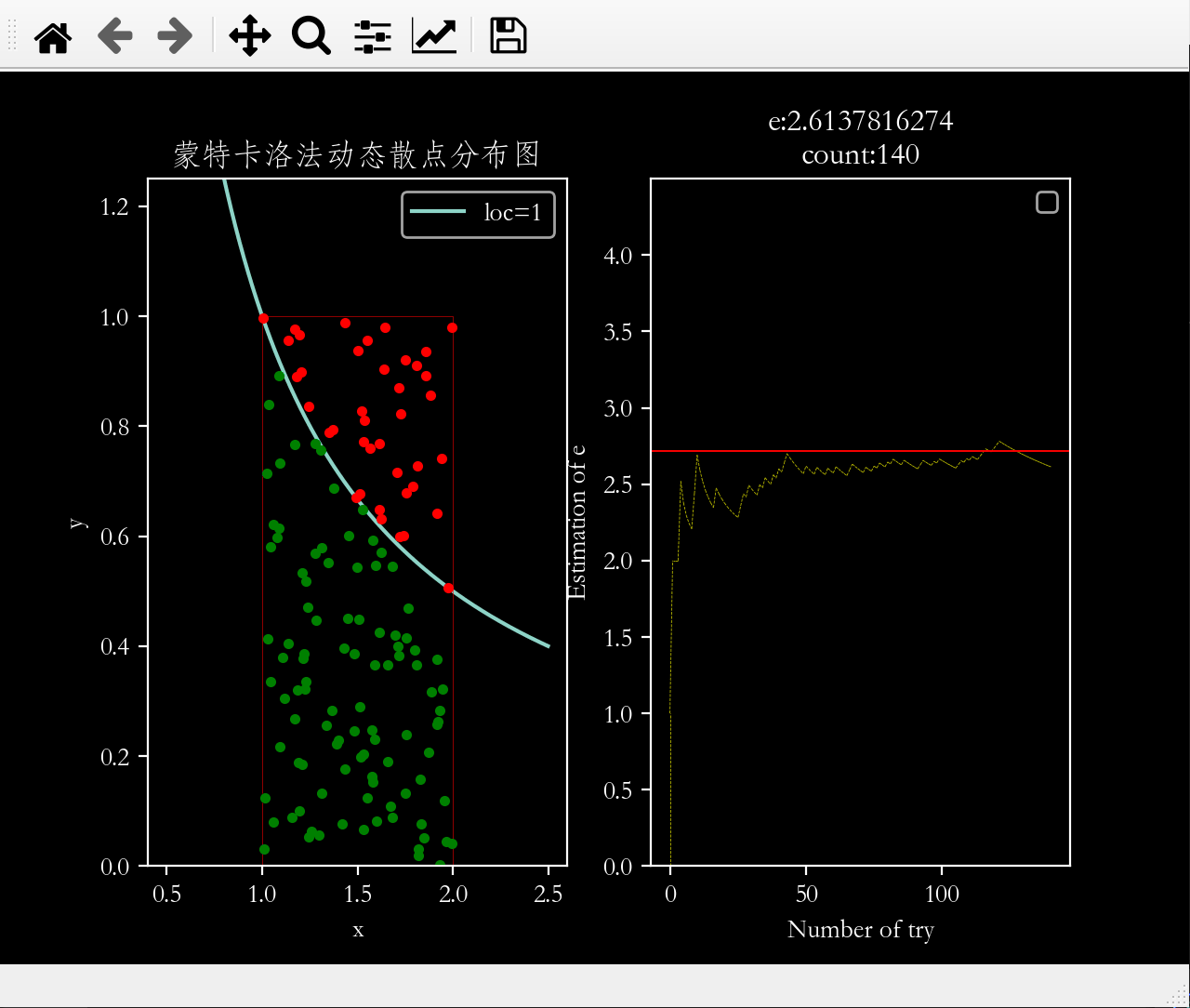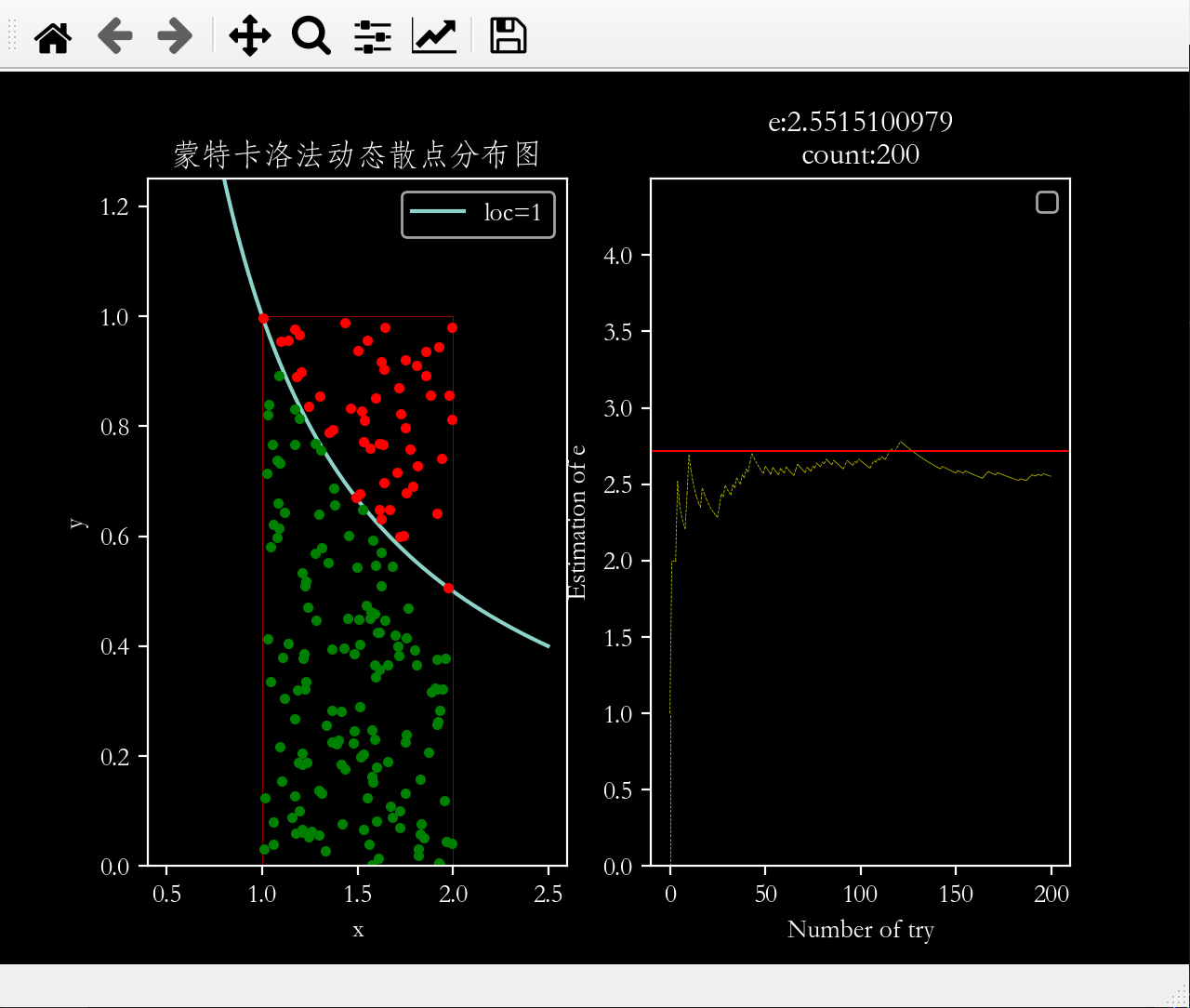
文章插图
图片2：蒙特卡洛法动态散点分布图
3 python的e求近似值==求阶乘法
=========================
3.1 代码1：
#计算e的值（精度为10**-6 ， 可调节 ， 最大50 ， 即小数点后50位）sum,tmp = 1,1for i in range(1,100):#100 ， 为取值最小17 ， 代码2有讲解tmp*=isum += 1/tmpprint("e的近似值（精度为10**-6）为%.6f"%sum)print("e的近似值（精度为10**-9）为%.9f"%sum)print("e的近似值（精度为10**-29）为%.29f"%sum)print("e的近似值（精度为10**-69）为%.69f"%sum)3.2 代码1结果：
#e的近似值（精度为10**-6）为2.718282#e的近似值（精度为10**-9）为2.718281828#e的近似值（精度为10**-29）为2.71828182845904553488480814849#e的近似值（精度为10**-69）为2.7182818284590455348848081484902650117874145507812500000000000000000003.3 代码2：
n = int(input())sum = 0def jc(a):#求阶乘num = 1for i in range(a + 1):if i != 0:num *= ireturn numfor i in range(n + 1):sum += 1 / jc(i)print('{:.50f}'.format(sum))3.4 结果
n为输入非负整数 n（≤1000）17 #为最小n ， 大于17的n值基本不变2.7182818284590455348848081484902650117874145507812516 #＜17的数值改变2.718281828459042870349549048114567995071411132812504 图片1的代码
import matplotlib.pyplot as plt#级数 1+1/1!+1/2!+?+1/n!+? 来近似计算x = []y = []#计算e的值（精度为10**-50）edata,tmp = 1,1for i in range(1,50):x.append(i)tmp*=iy.append(edata)edata += 1/tmpplt.plot(x, y)plt.title('e自然常数（欧拉数）（小数点后50位）≈：\n{:.50f}'.format(edata))plt.show()5 图片2的说明
===========
5.1 源代码来自
#2019-3-14 张子豪 同济大学 感谢原作者#源代码有报错 ， 修改bug ， 并对代码进行注释、修改、整理5.2 源代码bug
No handles with labels found to put in legend./home/xgj/Desktop/python-e/2.py:35: MatplotlibDeprecationWarning: Adding an axes using the same arguments as a previous axes currently reuses the earlier instance.In a future version, a new instance will always be created and returned.Meanwhile, this warning can be suppressed, and the future behavior ensured, by passing a unique label to each axes instance.plt.subplot(121)......（省略）5.3 解决bug思路
#参考文章6 图片2代码
=========
6.1 第1步：导入模块
import randomimport matplotlib.pyplot as pltimport numpy as np6.2 第2步：初始化参数设置
#plt背景颜色定义 ， 一定放在前面plt.style.use('dark_background')DARTS = 300#可自定义 ， 源代码1024*1024 ， 太大了counts = 0 # 落在曲线下方的点数e = 0 # e的计算值xs = [0,0]ys = [0,0]#初始化定义画布 ， 一行2个子图axfig, (ax1, ax2) = plt.subplots(1, 2)6.3 第3步：子图1=ax1
# 开始画左边的图：撒点估计曲线下方的面积x = np.arange(0.5,2.5,0.001)ax1.set_ylim(0,1.25) # y轴坐标范围ax1.set_xlabel('x') # x轴标签ax1.set_ylabel('y') # y轴标签ax1.plot(x,1/x) # 绘制反比例函数曲线ax1.legend(['loc=1']) # 在右上角增加图例ax2.legend(['y = 1 / x']) # 图例的内容ax1.plot([1,1,2,2],[0,1,1,0],'r',linewidth=0.2) # 绘制撒点范围框ax1.set_title('蒙特卡洛法动态散点分布图') # 图的标题动态更新6.4 第4步：联动子图1和子图2
#4-1 子图1的散点图for i in range(DARTS):x = random.uniform(1,2)y = random.uniform(0,1)if y < 1/x: # 点落在曲线下方counts += 1ax1.plot(x,y,'g.')else: # 点落在曲线上方ax1.plot(x,y,'r.')if counts>0:e = pow(2,i/counts)#4-2 子图2设置# 开始画右边的图：e的计算值随投掷次数的关系xs[0] = xs[1] # 上一个e值与下一个e值 ， 通过xs与ys列表中的两个元素进行两点连线xs[1] = iys[0] = ys[1]ys[1] = eax2.set_ylim(0,4.5) # y轴坐标范围ax2.set_xlabel('Number of try') # x轴标签ax2.set_ylabel('Estimation of e') # y轴标签ax2.set_yticks(np.arange(0,4.5,0.5)) # y轴刻度线ax2.set_title('e:{:.10f}\ncount:{}'.format(e,i)) # 图的标题动态更新# 绘制2.71828参考线ax2.axhline(np.e,linewidth=0.05,color='r')# 绘制e的计算值随撒点次数变化的曲线ax2.plot(xs,ys,'y--',linewidth=0.3)#子图1和子图2交互（ax1与ax2交互）plt.ion() # 保持图像处于交互更新状态plt.pause(0.2) # 控制撒点速度