PNAS：音乐刺激调制神经节律的两种理论模型( 二 ) 来源：PHIgroup导读过去许多研究

在每个实验中，这两个模型都会对频率间的PCM产生一个单一预测。为了评估相对数据的预测精度，使用了两种方法：(I)CIs和(II)高斯拟合，最后使用AIC（Akaike information criteria,赤池信息准则）来比较诱发模型和神经振荡模型对于MEG神经活动的拟合能力。
用什么证据回答
4.1 模型分析
示例模型输出和PCM分析如图3所示。 PCM清楚地区分了这两种模型。在诱发模型(图3A)下，模型输出和刺激之间的相位滞后强烈依赖于音符频率，随着频率的增加，模型输出和刺激之间的相位差也会增加，相位差从0.5nps到8nps几乎在整个周期移动，得到更小的PCM值（PCM = 0.17）。而在振荡模型中，相位滞后仍然集中(图3B) ，因此振荡模型的同步相位范围比诱发模型的小，显示了比诱发模型中看到的更长的向量(PCM=0.66) 。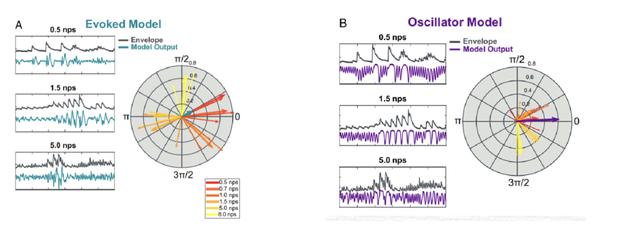
文章插图
* 图3
4.2 试验1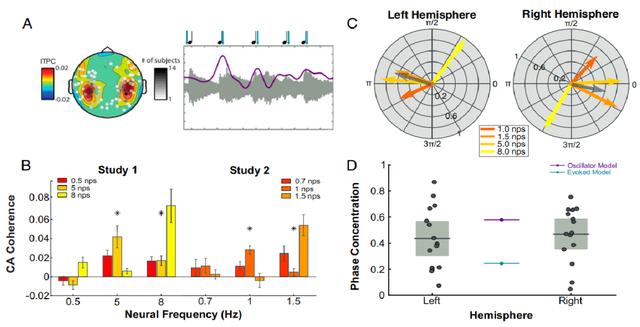
文章插图
* 图4
对这些数据的分析使用了ITPC (intertrial phase coherence ，试验间相位一致性) ，这是一种在试验中测量相位一致性的指标，但并不直接与刺激相关，其揭示了频率为1至8赫兹的神经调制结果（图4A）。在两个研究中(研究1：0.5、5和8nps；研究2：0.7、1和1.5nps)计算CACoh值并且分别进行比较(图4B) 。只有在大于1 nps及以上的值才会显示出有意义的结果，因此只考虑同步成功的1到8 nps的频率。（图4C）显示了MEG神经活动每种频率的受试者之间的平均相位延迟，并且比较了两种模型的预测效果（图4D），发现诱发模型的预测值明显超出了双侧大脑半球平均PCM的CI ，而神经振荡模型的预测是在边界上，在左半球CI之外，右半球CI之内。
4.3 试验2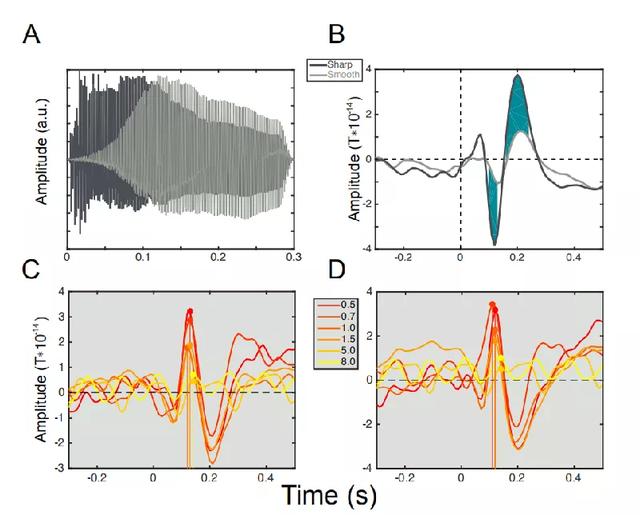
文章插图
* 图5
试验2的必要性：一些经典的研究表明，诱发反应的幅度随着刺激率的变化而变化。随着刺激率达到2赫兹而降低，然后随着刺激率的继续增加而增加。在试验2中，通过查看峰值延迟如何受音符频率影响来直接解决这个问题。如果诱发模型对PCM的低估是由于不同刺激频率的峰值潜伏期的变化导致的，那么预计峰值响应的潜伏期应该随着音刺激频率的增加而减少。但是（图5）表明响应的峰值幅度随着刺激频率的增加而减小，而M100的峰值延迟则增大，这种效应预计将比诱发模型预测的更有可能降低脑磁图数据的PCM值。因此，平滑声音刺激可以减少这种混淆。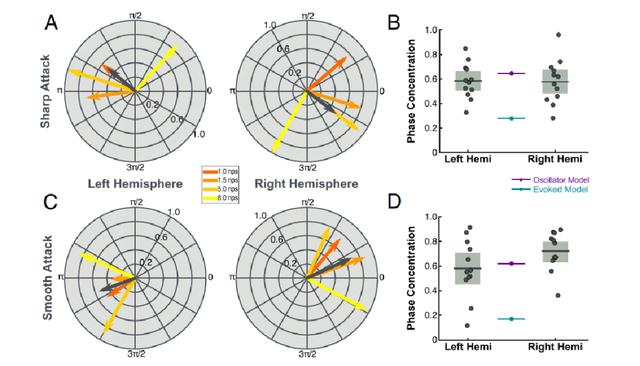
文章插图
* 图6
本研究分别计算了两种条件下的PCM值，尖锐刺激条件下如图6A ，平滑刺激条件下如图6C 。尖锐的声音刺激发现了与试验1相似的结果，进一步验证了试验1 。而对于平滑刺激条件下，将左脑和右脑皮层神经活动的CIs与模型预测进行了比较，发现诱发模型的预测明显超出脑磁图神经活动的CIs ，但神经振荡模型的预测在它们的上界范围内，如图6D 。在这种情况下，神经振荡模型预测始终在CIs内，而诱发模型预测始终在CIs之外。因此，试验2进一步验证了神经振荡模型能更好地预测皮层对于音乐的外界节律-同步化神经振荡的现象。
结论
本研究发现参与者的PCM与神经振荡模型的匹配比与诱发模型的匹配更好，证明了听觉皮层存在神经振荡机制，可能与自下而上的诱发反应相协调。并且通过控制尖锐和平滑的音乐刺激来减少诱发信号的幅度，进一步表明神经振荡模型比纯粹的诱发模型能更好地预测脑磁图神经活动的PCM 。此外，本研究还发现神经振荡反应和诱发反应的相对权重部分取决于音符的幅值。
主要问题

诱发模型以及神经振荡模型的建立具有一定的局限性，例如在诱发模型中，仅利用一个平均后的kernel与听觉刺激包络进行拟合。
这个研究中使用的诱发模型过于简单，如果在诱发模型中考虑到不同刺激频率下的kernel差异，这样改良的诱发模型可能不一定比振荡模型的预测性差。

有什么启发
神经机理研究往往从数据出发建立模型进行预测，而这篇研究根据经典神经科学理论，提出数学模型，再通过评价参数（PCM）比较两种模型的预测效果，通过这篇文章学习了比较典型的计算神经科学研究思路。