通过代码学 Sutton 强化学习：SARSA、Q-Learning 时序差分算法训练 CartPole 来源|MyEncyclopediaTDLearning本质上

文章插图
来源 | MyEncyclopedia
TD Learning本质上是加了bootstrapping的蒙特卡洛（MC），也是model-free的方法，但实践中往往比蒙特卡洛收敛更快。我们选取OpenAI Gym中经典的CartPole环境来讲解TD 。
文章插图
CartPole OpenAI 环境【通过代码学 Sutton 强化学习：SARSA、Q-Learning 时序差分算法训练 CartPole】如图所示，小车上放了一根杆，杆会根据物理系统定理因重力而倒下，我们可以控制小车往左或者往右，目的是尽可能地让杆保持树立状态。
文章插图
CartPole OpenAI Gym
CartPole 观察到的状态是四维的float值，分别是车位置，车速度，杆角度和杆角速度。下表为四个维度的值范围。给到小车的动作，即action space ，只有两种：0 ，表示往左推；1 ，表示往右推。
文章插图
文章插图
离散化连续状态从上所知， CartPole step 函数返回了4维ndarray ，类型为float32的连续状态空间。对于传统的tabular方法来说第一步必须离散化状态，目的是可以作为Q table的主键来查找。下面定义的State类型是离散化后的具体类型，另外 Action 类型已经是0和1 ，不需要做离散化处理。
State = Tuple[int, int, int, int]Action = int离散化处理时需要考虑的一个问题是如何设置每个维度的分桶策略。分桶策略会决定性地影响训练的效果。原则上必须将和action以及reward强相关的维度做细粒度分桶，弱相关或者无关的维度做粗粒度分桶。举个例子，小车位置本身并不能影响Agent采取的下一动作，当给定其他三维状态的前提下，因此我们对小车位置这一维度仅设置一个桶（bucket size=1）。而杆的角度和角速度是决定下一动作的关键因素，因此我们分别设置成6个和12个。
以下是离散化相关代码，四个维度的 buckets=(1, 2, 6, 12) 。 self.q是action value的查找表，具体类型是shape 为 (1, 2, 6, 12, 2) 的ndarray 。
class CartPoleAbstractAgent(metaclass=abc.ABCMeta): def __init__(self, buckets=(1, 2, 6, 12), discount=0.98, lr_min=0.1, epsilon_min=0.1): self.env = gym.make('CartPole-v0') env = self.env # [position, velocity, angle, angular velocity] self.dims_config = [(env.observation_space.low[0], env.observation_space.high[0], 1), (-0.5, 0.5, 1), (env.observation_space.low[2], env.observation_space.high[2], 6), (-math.radians(50) / 1., math.radians(50) / 1., 12)] self.q = np.zeros(buckets + (self.env.action_space.n,)) self.pi = np.zeros_like(self.q) self.pi[:] = 1.0 / env.action_space.n def to_bin_idx(self, val: float, lower: float, upper: float, bucket_num: int) -> int: percent = (val + abs(lower)) / (upper - lower) return min(bucket_num - 1, max(0, int(round((bucket_num - 1) * percent)))) def discretize(self, obs: np.ndarray) -> State: discrete_states = tuple([self.to_bin_idx(obs[d], *self.dims_config[d]) for d in range(len(obs))]) return discrete_statestrain 方法串联起来 agent 和 env 交互的流程，包括从 env 得到连续状态转换成离散状态，更新 Agent 的 Q table 甚至 Agent的执行policy ， choose_action会根据执行 policy 选取action 。
def train(self, num_episodes=2000): for e in range(num_episodes): print(e) s: State = self.discretize(self.env.reset) self.adjust_learning_rate(e) self.adjust_epsilon(e) done = False while not done: action: Action = self.choose_action(s) obs, reward, done, _ = self.env.step(action) s_next: State = self.discretize(obs) a_next = self.choose_action(s_next) self.update_q(s, action, reward, s_next, a_next) s = s_nextchoose_action 的默认实现为基于现有 Q table 的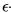
文章插图
-greedy 策略。
def choose_action(self, state) -> Action: if np.random.random < self.epsilon: return self.env.action_space.sample else: return np.argmax(self.q[state])抽象出公共的基类代码 CartPoleAbstractAgent 之后， SARSA、Q-Learning和Expected SARSA只需要复写 update_q 抽象方法即可。