重复测量数据分析系列：混合效应模型基础混合效应模型的不同称谓多层

混合效应模型的不同称谓多层混合效应线性模型（Multilevel Mixed-Effect Linear Model）；多水平模型（Multilevel Model），分层线性模型（Hierarchical Linear Model）；混合效应模型（Mixed Effect Model），混合线性模型（Mixed Linear Model）；随机截距-斜率发展模型（Random intercept and slop Model ， RIS Model ）；随机效应模型（Random Coefficient Model），随机系数模型（Random Coefficient Model）；随机斜率模型（Random Slop Model）；随机截距模型（Random intercept Model），方差成分模型（Variance Component Model）；残差方差/协方差模式模型（Residual Covariance Pattern Model）……
简单地说，混合效应模型（Mixed Effect Model）/混合线性模型（Mixed Linear Model）是既包含固定效应又包括随机效应的模型。
固定效应（fixed effect）和随机效应（random effect）【重复测量数据分析系列：混合效应模型基础】在很多统计方法都能看到固定效应（fixed effect）和随机效应（random effect）的身影，比如方差中的固定因素和随机因素， Meta分析中的固定效应和随机效应，以及多水平模型中的固定截距/斜率和随机截距/斜率。通俗地理解，固定效应就是不变的效应，固定因素就是其效应在不同的组不会发生变化的因素，而随机效应因素则是指其效应在不同的组会不同的因素。定义上看Fixed effect factor: Data has been gathered from all the levels of the factor that are of interest.Random effect factor: The factor has many possible levels, interest is in all possible levels, but only a random sample of levels is included in the data 。固定因素指的是该因素的各种取值水平在样本中都出现了,而随机因素的各个水平只是从总体中抽样而来，该因素所有的取值水平并没有都出现。
举个栗子，两组标准相同的无并发症的单纯原发性高血压患者分别采用替米沙坦片和苯磺酸氨氯地平片进行降压，如果你只是想看下替米沙坦片和苯磺酸氨氯地平片的疗效有无差异，那么治疗药物这个分组因素就是固定因素；但如果你的目的是想比较ARB和CCB的差异， ARB和CCB类降压药都有很多药物，只是替米沙坦和氨氯地平刚好是你选择的代表ARB和CCB的药物而已，你想把对这两个代表药物的研究结果推广到对所有其他水平都适用，这时候治疗药物这个分组因素就应看做随机因素。
混合效应模型的数据表现为分级或多层结构，低层级单位嵌套或集聚于高层级单位之中，高层次单位内同一个水平的观测数据常常存在一定的集聚性、相关性，即组内观测是非独立的，从而使组间产生了差别，此即所谓的“组内异质，组间同质” 。比如大型的多中心临床试验，个体数据嵌套于各个临床中心，每个中心的受试者可能存在相关性；再比如重复测量数据，个体内数据嵌套于每个个体内，每个个体内的多次测量数据可能存在相关。从这个角度上，混合效应模型也被称为多水平模型（Multilevel Model）、分层线性模型（Hierarchical Linear Model）。此名称中的“水平”与因素的某个水平意义是不同的，叫多层级模型可能更合适。
在混合效应模型中，固定效应可以直接估计得到，用均数描述，类似于回归系数，如在平均回归线回中的截距表示平均截距β0 ，斜率即平均斜率β1；随机效应不是直接估计,用方差进行描述，以随机截距或者随机斜率的形式呈现，反应在它们的方差和协方差估计值中。数据的分层结构使得每一层都会有一个残差协方差结构，个体间（高层级单位）残差协方差常用G表示，矩阵G通常为随机截距与随机斜率的方差协方差矩阵，个体内（低层级单位）残差协方差常用R表示。在纵向数据的发展模型中， y的均值或期望值是通过固定效应的β来分析的，而y的方差则是通过G（随机效应的方差协方差）矩阵和R （低层级单位的方差协方差）矩阵来分析。
混合效应模型的种类根据截距和斜率是否随机，混合效应模型可以有四种情况：①固定截距+固定斜率；②固定截距+固定斜率；③随机截距+固定斜率；④随机截距+随机斜率。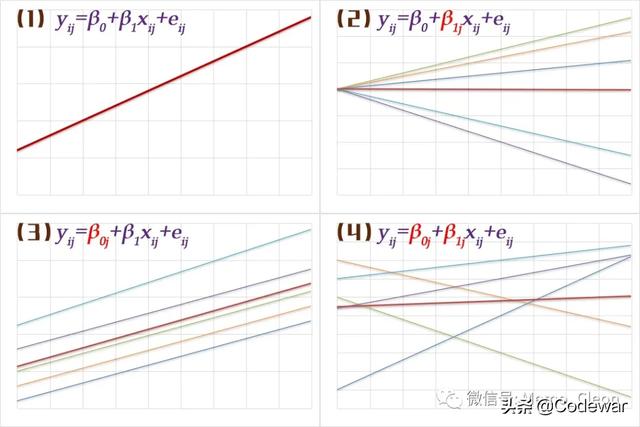
文章插图
（1）固定截距+固定斜率：这种情况实际上是混合线性模型的特殊情况，采用一般线性模型进行分析就可以了。
（2）固定截距+随机斜率：各组回归线截距相同，但斜率不同，斜率随组的变化而变化。
（3）随机截距+固定斜率：组内回归的截距随组变化而变化但斜率相同，即低层级自变量的斜率在不同的组里面都是一致的。虽然实际中这种绝对一致（斜率相等）的情况很少存在，但在统计学上的相等并不等同于绝对相等，可以通过显著性检验来确定组间斜率是否保持一致。