边界条件|如何快速从算法萌新逆袭成为码神？算法萌新在刷力扣时

文章插图
算法萌新在刷力扣时，虽然已有一些算法基础但仍然出现一题都做不出来的现象，经常有以下困惑：

1.代码写了又删、删了又写，写到一半才发现逻辑走不通，没有整体思路。
2.不能分析出题目需要用到什么算法。

那么该如何解决这些问题呢？

文章插图
先用伪代码写出逻辑，再补全小段代码力扣上的 Easy 题分两种，一种是不需要算法逻辑，只要按照题目描述将代码敲出来即可。另一种是不拐弯抹角，只需要一种标准算法即可。
对于第一类 Easy 题，我们可以先根据题意将逻辑理顺，写出伪代码，然后逐步补全小段的代码。
例如：1029. 两地调度力扣
题目描述很清晰，看完题目我们可以先想出代码的流程：

文章插图
将流程写出来后，再逐步补全代码：

文章插图
这就好比先规划好目的地，再一小段一小段的达成目标。开发者要写一个功能单一的函数是比较简单的，这就像一个小步快跑的过程。
再比如：1030. 距离顺序排列矩阵单元格力扣
同样的，我们先根据题目描述写出代码流程：

文章插图
然后逐步补全代码

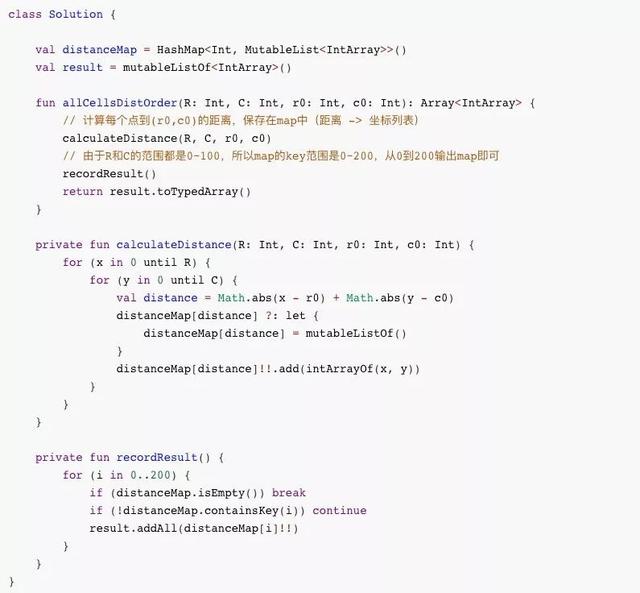文章插图
伪代码可以帮助我们明确自己需要做什么，这一点和”测试驱动开发“（TDD）的思想是一致的。我们在做的时候就会知道：“只要我完成了这些步骤，就可以实现我要的效果。 ” 而不是盲目的写了又删、删了又写。

文章插图
判断题目描述是否满足某个算法所需的条件新手在阅读算法题目时，经常会分析不出题目需要用哪一种算法来解决。主要的原因在于阅读的题目太少，对每一类算法适用的场景不熟悉。
这个问题很好解决，力扣对每个题目都设置有相应的 tag ，我们可以按照力扣对题型的分类，先看同一类题目。对这类算法题目的描述就会有个比较清晰的认识。如同学习英语一样，看多了倒装句，一眼就能看出倒装句的结构；看多了感叹句，一眼就能看出感叹句的结构。这也是一个熟能生巧的过程，需要花时间去了解、总结每类算法的特点，量变引起质变。

文章插图
例如，我们点击“二分查找”标签，显示如下：

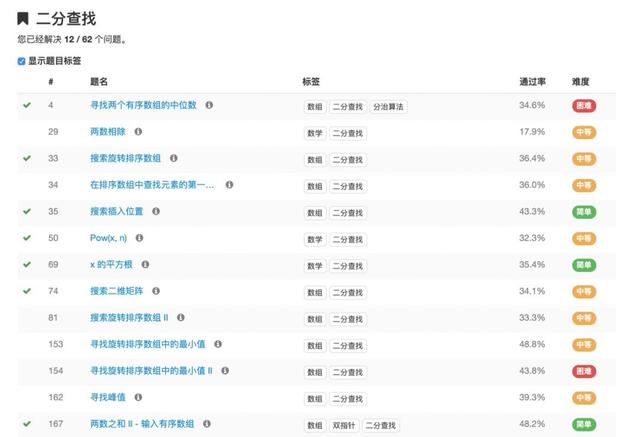文章插图
粗略浏览，可以发现，二分查找的题目中很多都带有“有序“、”排序“字样。接下来我们进一步分析题目，先从简单题开始：
35. 搜索插入位置力扣
这道题就属于上文所说的只需要一种标准算法的 Easy 题。没有任何的拐弯抹角，一道典型的二分题目。题目场景有以下特点：

数组是有序的
答案是有界的，在[0, nums.size]之间
目标值越大，答案越大，这里有一个单调递增的关系

二分法有标准的套路 (本例使用的 Kotlin 语言，不过算法跟编程语言关系不大)：

文章插图
如果你熟悉这个套路的话，我们可以很快写出答案：

文章插图
再来一道中等题目练练手：
33. 搜索旋转排序数组力扣
分析题目，可知：

数组旋转之前是有序的
答案是有界的，在[0, nums.size]之间
目标值越大，答案越大，这里有一个单调递增的关系

与标准的二分题目相比，只多了一个条件：有序数组被旋转了。只要先将数组旋转回来，再用二分法求出结果，再根据旋转的位置调整下标即可。其实中等题目很多都是在典型的算法题上面拐一个弯，困难题目一般是糅合两种算法，万变不离其宗。此题解决方案如下：