掌握这些数学函数，你会在算法效率的分析时经常用到( 二 ) 如何进行算法分析呢？最简单

文章插图
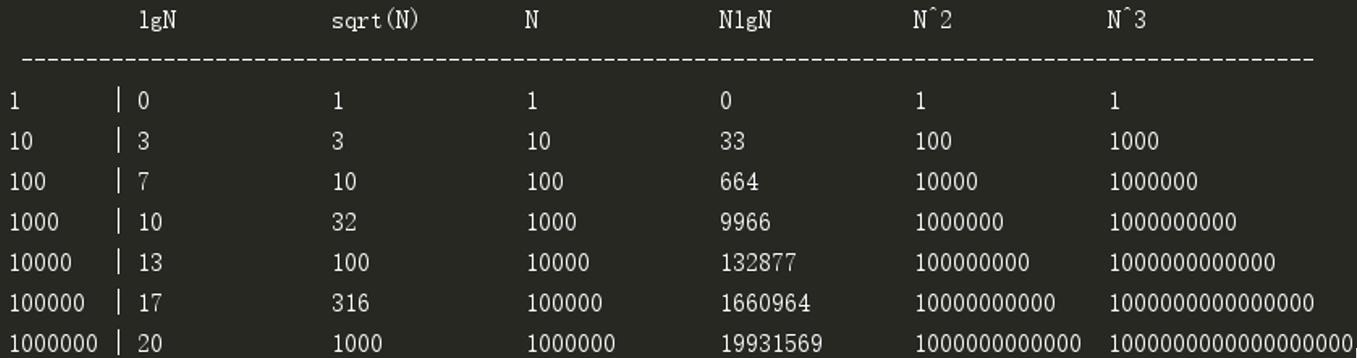
图 2 告诉我们，该问题规模是 1 的时候，所有算法都同样有效，问题规模越大，不同复杂度的算法运行效率相差得越大。
2^N 增长得太过迅猛，作为一个另类单独列出。
▼ 代码 3 2^N 的增长
01 for N in range(10, 110, 10):02 print('2**{0} = {1}'.format(N, 2 ** N))运行结果如图 3 所示。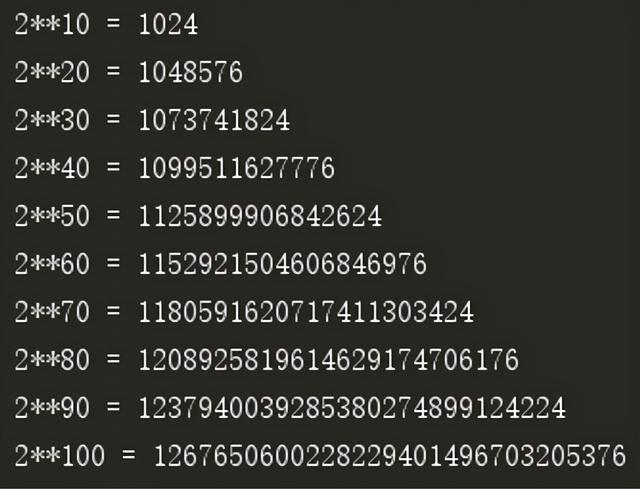
文章插图
▲ 图 4.3 2^N 的增长
这些运行结果告诉我们，有些时候，选择正确的算法是解决问题的唯一途径。对于函数的输出结果来说，如果把 100 看作 1 秒，那么 10000 就是 100 秒，超过 1 分半。这意味着对于一个规模是 1000000 的问题来说，一个是 lg?N 复杂度的算法可以立刻得出结果， √N 复杂度的算法耗时约 10 秒， N 复杂度的算法耗时将超过 2.7 小时， N^3 复杂度则需要 3 万多年！也许我们可以忍受一运行 10 秒或 2.7 小时的程序，但一定没法容忍有生之年看不到结果的程序。
文章插图
上文 [遇见] 授权节选自北大出版社《程序员数学从零开始》
【掌握这些数学函数，你会在算法效率的分析时经常用到】270余幅插图+90余段Python代码+20余个原理剖析，教你学会程序员必须掌握的数学及算法背后的数学原理。