机器学习的未来就在这里：高斯过程和神经网络是等价的

文章插图
> Photo by Mohamed Nohassi on Unsplash
高斯进程已经存在了一段时间，但它只是在过去5-10年，有一个大的复苏，其兴趣。部分原因是求解的计算复杂：由于他们的模型需要矩阵反转，复杂性是 O（n3），很难更快地获得。正因为如此，它一直难以解决一段时间，因为计算能力一直如此薄弱，但在过去的几年里，有这么多的研究和资金背后的ML ，它变得更加可能。
高斯过程最酷的特征之一是它们非常非常相似的神经网络。事实上，众所周知，高斯进程（GP）相当于单层完全连接的神经网络，其参数比其参数更具有 i.i.d.。
我想说清楚这一点：下面的证据很简单，但它具有深远的影响。中央极限定理可以统一明显复杂的现象，在这种情况下，性能最好的模型可以被视为机器学习模型的子集，该模型的领域尚未完全成熟。
是的，对GP的研究一直经受住考验，但只是在过去几年中，研究人员才开发出能够对非线性模式（如跳跃）进行特征化的深高斯过程，而DNN的这种模式是做成的（特别是能够对XOR逻辑进行建模）。因此，从这一点，我们可以看到，有这么多收获。
我一直想研究一下这个证据，下面很简单。以下文章由李等人在谷歌脑的报纸上取，因此我要感谢他们让本文如此方便。
有点符号注意：您不能对"媒体"上的所有内容进行下标，因此，如果您看到下划线（M_l），则假设这意味着 M 与 l 作为下标。所以一个M_i + 米
考虑使用隐藏宽度层（对于层 L）N_l L 层完全连接的神经网络。让 x ∈ Rd?输入到网络，让 z l 表示其输出（在层 L）。 l'th 层中激活的 i'th 组件表示为 xli 和 zli 。 l'th 层的权重和偏置参数具有 iid 的零值和偏置参数，并假定它们具有零均值和 σ 2_w/N_l 。
文章插图
> Photo by Maximalfocus on Unsplash
神经网络现在我们知道神经网络输出（zli）的 i'th 组件的计算方式如下：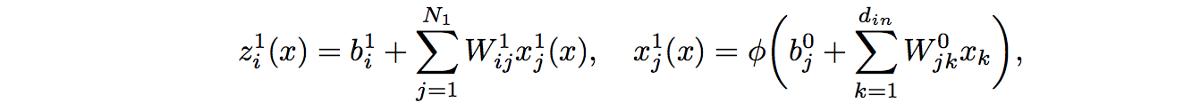
文章插图
我们显示了对输入 x 的依赖性。由于权重和偏置参数假定为 iid ，因此 xli 和 xli' 的 pos 激活函数对于 j=/j' 是独立的。
现在，由于 zli（x）是 iid 项的总和，它遵循中央限制定理，因此在无限宽度（N1-> ∞）的限制中， zli（x）也因此高斯分布。
高斯进程同样，从多维CLT ，我们可以推断比任何有限集合的变量z将是联合多变量高斯，这恰好是我们高斯过程的确切定义。
因此，我们可以得出结论， zli（x）=GP（μ 1 ， K1）是一个高斯过程，均值为μ 1 ， K1为协方差，它们本身与 i 无关。由于参数的均值为零，因此μ 1=0 ，但 K1（x ， x'）如下所示：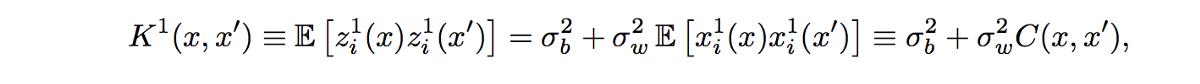
文章插图
其中，通过针对W0和b0的分布进行整合获得这种协方差。请注意，由于 i=/=j 的任何两个 zli 和 zlj 都是共同的高斯，并且零协方差，因此尽管使用了隐藏层产生的相同功能，它们仍保证是独立的。
文章插图
> Photo by Birmingham Museums Trust on Unsplash
一些证据是简单和合乎逻辑的，中央极限定理的魔力是，它统一了高斯分布下的一切。高斯分布是伟大的，因为边缘化和调节变量（或维度）导致高斯分布和功能形式是相当简单的，所以事情可以浓缩成封闭形式的解决方案（所以很少需要优化技术）。
让我知道你是怎么找到我的逻辑，问问题，如果你有任何问题，请让我知道，如果我错过了什么！
随时了解我的最新文章！
【机器学习的未来就在这里：高斯过程和神经网络是等价的】(本文翻译自Tivadar Danka的文章《The Future of Machine Learning is Here》，参考：)