终极版AlphaGo，DeepMind新算法MuZero作者解读加速|苹果|收割|落地|特斯拉

译者：AI研习社（季一帆）
双语原文链接：MuZero Intuition
为庆祝Muzero论文在Nature上的发表，我特意写了这篇文章对MuZero算法进行详细介绍，希望本人能让你对该算法有一个直观的了解。更多详细信息请阅读原文。
MuZero是令人振奋的一大步，该算法摆脱了对游戏规则或环境动力学的知识依赖，可以自行学习环境模型并进行规划。即使如此，MuZero仍能够实现AlphaZero的全部功能——这显示出其在许多实际问题的应用可能性！
所有一切不过是统计MuZero是一种机器学习算法，因此自然要先了解它是如何使用神经网络的。简单来说，该算法使用了AlphaGo和AlphaZero的策略网络和值网络：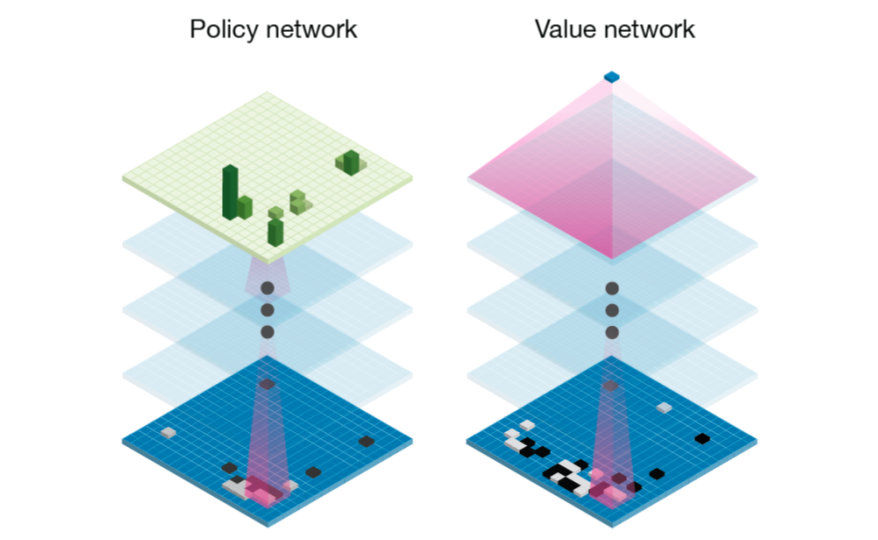

文章插图
策略和值的直观含义如下：

策略p(s,a)表示在状态s时所有可能的动作a分布，据此可以估计最优的动作。类比人类玩家，该策略相当于快速浏览游戏时拟采取的可能动作。
值v(s)估计在当前状态s下获胜的可能性，即通过对所有的未来可能性进行加权平均，确定当前玩家的获胜概率。

这两个网络任何一个都非常强大：只根据策略网络，能够轻易预测每一步的动作，最终得到良好结果；只依赖值网络，始终选择值最高的动作。但是，将这两个估计结合起来可以得到更好的结果。
取胜之路与AlphaGo和AlphaZero相似，MuZero也使用蒙特卡洛树搜索方法（MCTS）汇总神经网络预测并选择适合当前环境的动作。
MCTS是一种迭代的，最佳优先的树搜索过程。最佳优先意味着搜索树的扩展依赖于搜索树的值估计。与经典方法（如广度优先或深度优先）相比，最佳优先搜索利用启发式估计（如神经网络），这使其在很大的搜索空间中也可以找到有效的解决方案。
MCTS具有三个主要阶段：模拟，扩展和反向传播。通过重复执行这些阶段，MCTS根据节点可能的动作序列逐步构建搜索树。在该树中，每个节点表示未来状态，而节点间的边缘表示从一个状态到下一个状态的动作。
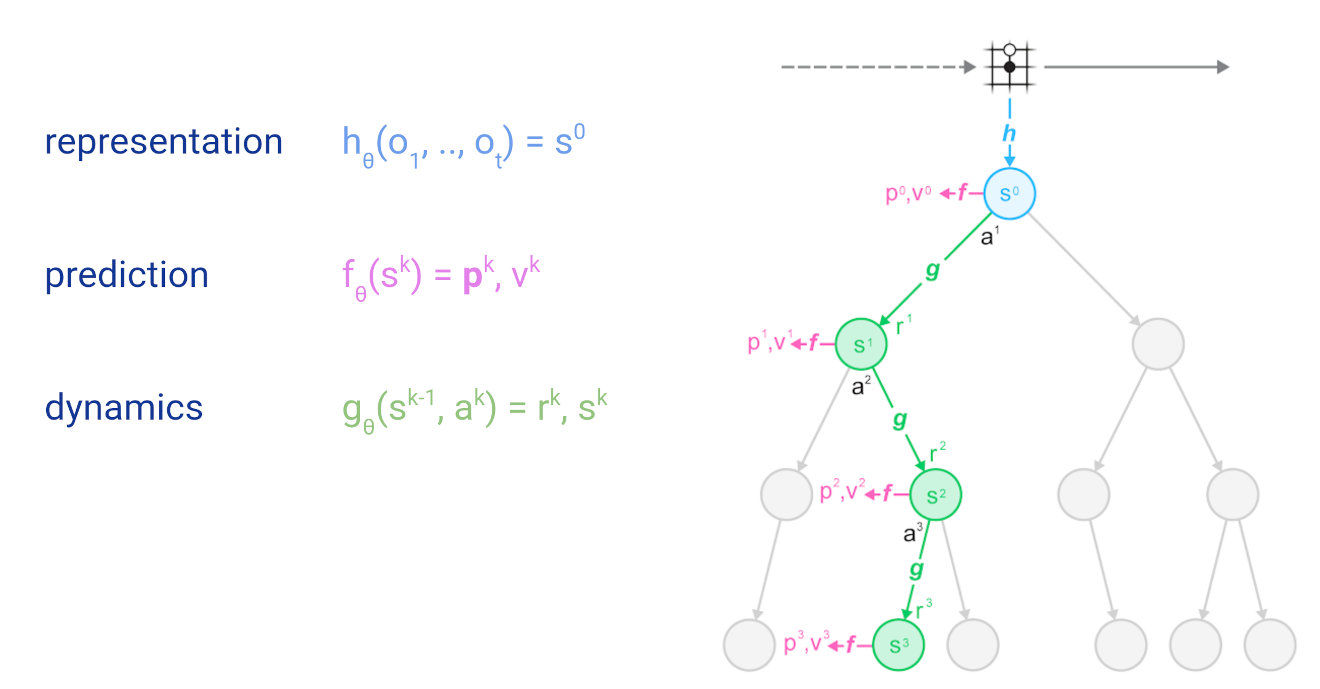
在深入研究之前，首先对该搜索树及逆行介绍，包括MuZero做出的神经网络预测：

文章插图
圆圈表示树节点，对应环境状态；线表示从一个状态到下一个状态的动作；根节点为当前环境状态，即围棋面板状态。后续章节我们会详细介绍预测和动力学函数。
模拟：从树的根节点出发（图顶部的淡蓝色圆圈），即环境或游戏的当前位置。在每个节点（状态s），使用评分函数U(s,a)比较不同的动作a，并选择最优动作。MuZero中使用的评分函数是将先前的估计p(s,a)与v(s')的值结合起来，即
其中c是比例因子，随着值估计准确性的增加，减少先验的影响。
每选择一个动作，我们都会增加其相关的访问计数n(s,a)，以用于UCB比例因子c以及之后的动作选择。
模拟沿着树向下进行，直到尚未扩展的叶子。此时，应用神经网络评估节点，并将评估结果（优先级和值估计）存储在节点中。
扩展：一旦节点达到估计量值后，将其标记为“扩展”，意味着可以将子级添加到节点，以便进行更深入的搜索。在MuZero中，扩展阈值为1，即每个节点在首次评估后都会立即扩展。在进行更深入的搜索之前，较高的扩展阈值可用于收集更可靠的统计信息。
反向传播：最后，将神经网络的值估计传播回搜索树，每个节点都在其下保存所有值估计的连续均值，这使得UCB公式可以随着时间的推移做出越来越准确的决策，从而确保MCTS收敛到最优动作。
中间奖励细心的读者可能已经注意到，上图还包括r的预测。某一情况（如棋盘游戏）在完全结束后提供反馈（获胜/失败结果），这样可以通过值估计进行建模。但在另外一些情况下，会存在频繁的反馈，即每次从一种状态转换到另一种状态后，都会得到回报r。
只需对UCB公式进行简单修改，就可以通过神经网络预测直接对奖励进行建模，并将其用于搜索。
其中，r(s,a)是指在状态s时执行动作a后观察到的奖励，而折扣因子γ是指对未来奖励的关注程度。
由于总体奖励可以时任意量级的，因此在将其与先验奖励组合之前，我们将奖励/值估计归一化为区间[0,1]：
其中，q_min和q_max分别是整个搜索树中观察到的最小和最大r(s,a)+γ?v(s')估计。
过程生成
重复执行以下过程可实现上述MCTS：