漫话：如何给女朋友解释为什么计算机中 0.2 + 0.1 不等于 0.3？( 三 ) 作者|漫话编程来源|漫话编程（ID：mhco

IEEE 754规定了四种表示浮点数值的方式：单精确度（32位）、双精确度（64位）、延伸单精确度（43比特以上，很少使用）与延伸双精确度（79比特以上，通常以80位实现）。
其中最常用的就是32位单精度浮点数和64位双精度浮点数。
IEEE并没有解决小数无法精确表示的问题，只是提出了一种使用近似值表示小数的方式，并且引入了精度的概念。
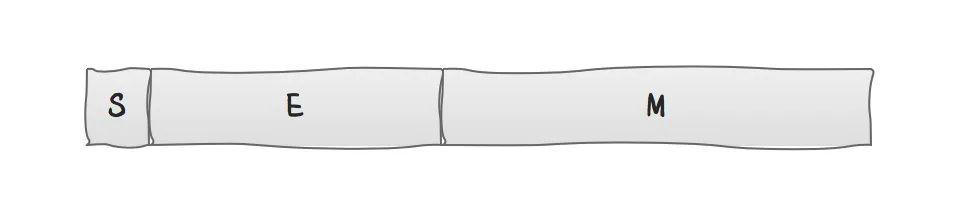
浮点数是一串0和1构成的位序列(bit sequence) ，从逻辑上用三元组{S,E,M}表示一个数N,如下图所示：
文章插图

S(sign)表示N的符号位。对应值s满足：n>0时， s=0; n≤0时， s=1 。
E(exponent)表示N的指数位，位于S和M之间的若干位。对应值e值也可正可负。
M(mantissa)表示N的尾数位，恰好，它位于N末尾。 M也叫有效数字位（significand）、系数位（coefficient）, 甚至被称作"小数" 。

则浮点数N的实际值n由下方的式子表示：

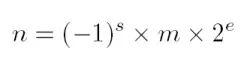文章插图
上面这个公式看起来很复杂，其中符号位和尾数位还比较容易理解，但是这个指数位就不是那么容易理解了。
其实，大家也不用太过于纠结这个公式，大家只需要知道对于单精度浮点数，最多只能用32位字符表示一个数字，双精度浮点数最多只能用64位来表示一个数字。
而对于那些无限循环的二进制数来说，计算机采用浮点数的方式保留了一定的有效数字，那么这个值只能是近似值，不可能是真实值。
至于一个数对应的IEEE 754浮点数应该如何计算，不是本文的重点，这里就不再赘述了，过程还是比较复杂的，需要进行对阶、尾数求和、规格化、舍入以及溢出判断等。
但是这些其实不需要了解的太详细，我们只需要知道，小数在计算机中的表示是近似数，并不是真实值。根据精度不同，近似程度也有所不同。
如0.1这个小数，他对应的在双精度浮点数的二进制为：0.00011001100110011001100110011001100110011001100110011001。
0.2这个小数0.00110011001100110011001100110011001100110011001100110011。
所以两者相加：

文章插图
转换成10进制之后得到：0.30000000000000004！

文章插图

文章插图
避免精度丢失
在Java中，使用float表示单精度浮点数， double表示双精度浮点数，表示的都是近似值。
所以，在Java代码中，千万不要使用float或者double来进行高精度运算，尤其是金额运算，否则就很容易产生资损问题。
为了解决这样的精度问题， Java中提供了BigDecimal来进行精确运算。

文章插图