二叉树：我是不是一棵二叉搜索树学习完二叉搜索树的特性了

学习完二叉搜索树的特性了，那么就验证一波
98.验证二叉搜索树给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

文章插图
思路要知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。
有了这个特性，「验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。」
递归法可以递归中序遍历将二叉搜索树转变成一个数组，代码如下：

vector vec;void traversal(TreeNode* root) {if (root == NULL) return;traversal(root->left);vec.push_back(root->val); // 将二叉搜索树转换为有序数组traversal(root->right);}

然后只要比较一下，这个数组是否是有序的，「注意二叉搜索树中不能有重复元素」。

traversal(root);for (int i = 1; i < vec.size(); i++) {// 注意要小于等于 ， 搜索树里不能有相同元素if (vec[i] <= vec[i - 1]) return false;}return true;

整体代码如下：

class Solution {private:vector vec;void traversal(TreeNode* root) {if (root == NULL) return;traversal(root->left);vec.push_back(root->val); // 将二叉搜索树转换为有序数组traversal(root->right);}public:bool isValidBST(TreeNode* root) {vec.clear(); // 不加这句在leetcode上也可以过 ， 但最好加上traversal(root);for (int i = 1; i < vec.size(); i++) {// 注意要小于等于 ， 搜索树里不能有相同元素if (vec[i] <= vec[i - 1]) return false;}return true;}};

以上代码中，我们把二叉树转变为数组来判断，是最直观的，但其实不用转变成数组，可以在递归遍历的过程中直接判断是否有序。
这道题目比较容易陷入两个陷阱：

陷阱1

「不能单纯的比较左节点小于中间节点，右节点大于中间节点就完事了」。
写出了类似这样的代码：
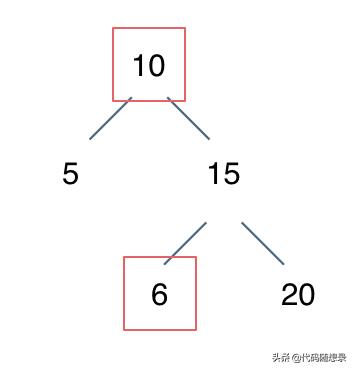
if (root->val > root->left->val } else {return false;}我们要比较的是左子树所有节点小于中间节点，右子树所有节点大于中间节点。所以以上代码的判断逻辑是错误的。
例如：[10,5,15,null,null,6,20] 这个case：

文章插图
节点10小于左节点5 ，大于右节点15 ，但右子树里出现了一个6 这就不符合了！

陷阱2

样例中最小节点可能是int的最小值，如果这样使用最小的int来比较也是不行的。
此时可以初始化比较元素为longlong的最小值。
问题可以进一步演进：如果样例中根节点的val 可能是longlong的最小值又要怎么办呢？文中会解答。
了解这些陷阱之后我们来看一下代码应该怎么写：
递归三部曲：

确定递归函数，返回值以及参数

要定义一个longlong的全局变量，用来比较遍历的节点是否有序，因为后台测试数据中有int最小值，所以定义为longlong的类型，初始化为longlong最小值。
注意递归函数要有bool类型的返回值，我们在二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？中讲了，只有寻找某一条边（或者一个节点）的时候，递归函数会有bool类型的返回值。
其实本题是同样的道理，我们在寻找一个不符合条件的节点，如果没有找到这个节点就遍历了整个树，如果找到不符合的节点了，立刻返回。