算法|算法：最大公共子串( 二 )

这是因为如果str1[m]==str2[n]，dp[m+1] [n+1]=dp[m] [n]+1，而对于str1中m为0，str2中n为0时，如果用dp[0] [0]来保存，则没有dp[-1] [-1]的元素（数组元素下标最小为0）。
因此都是用dp[m+1] [n+1]来标识str1[m]，str2[n]是否相等信息。
哦，好像是这样的哦，可是我还是有点迷糊。
没事儿，我画了张，你对照图看就能明白了。

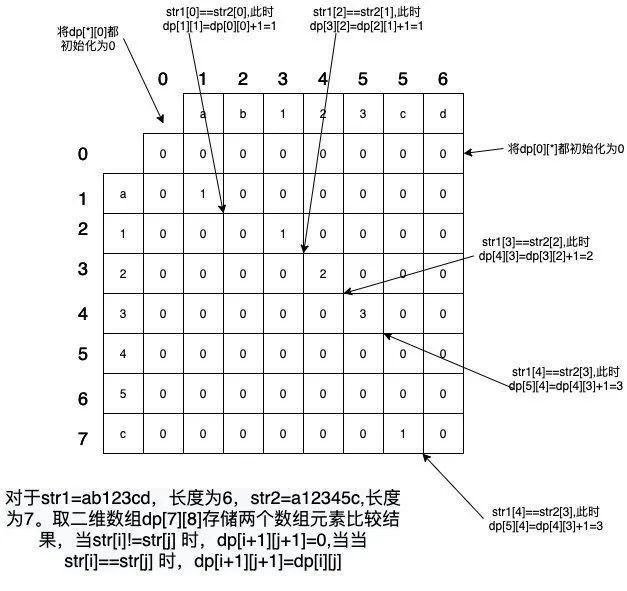
文章插图
代码实现如下：

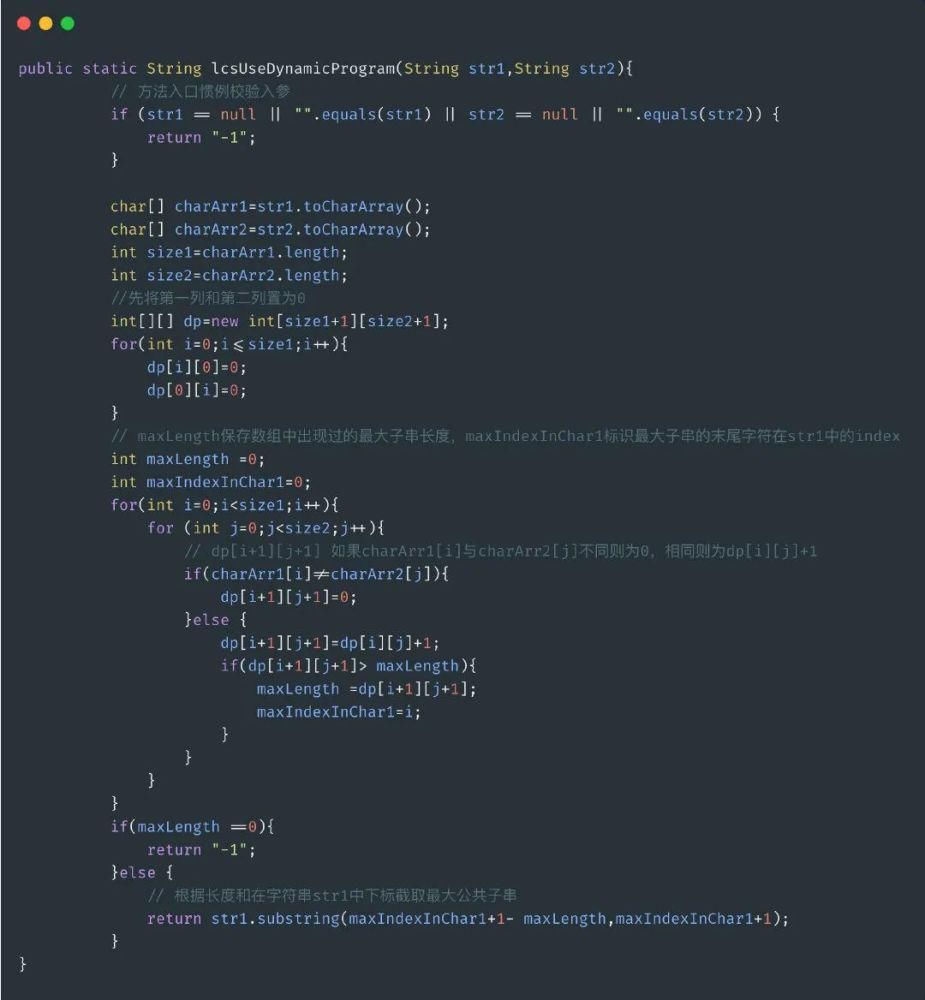
文章插图
你学会了吗，吒吒？
嗯，我看懂了哦，原来这么容易啊。
那你来总结下几种解法有什么区别吧？
嗯，第三种解法采取了动态规划的思想，解决的问题多数有重叠子问题这个特点，为了减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个二维数组中。
这样的话，复杂度就是O(m * n)，空间复杂度O(m * n)。
通过用空间换时间，使得字符串1与字符串2每个只是比较了一次！
那他和第一种、第二种解法又有什么不同呢？
他的执行效率优于第一种解法，而和第二种基于map定位的算法各有优劣。
当字符串重复率不高时而长度较长时，第二种算法（hash定位）时间和空间都优于第三种（动态规划）的算法。
当字符串中重复率逐渐升高时，第二种hash的算法效率明显下降，这时候，采用动态规划效率就更高。
不错啊，看来你完全掌握了哦，下次再教你一点新东西吧。
还是丙丙你教的好啊。好啊，下次我们再约！