用图形解释10种图形算法( 二 ) 快速介绍

· 用于网络中以解决最小延迟路径问题。
· 用于抽象机器中，以通过在不同状态之间进行转换来确定达到某个目标状态的选择（例如，可用于确定赢得一场比赛的最小可能次数）。
文章插图
> Image by Daniel Dino-Slofer from Pixabay
4.循环检测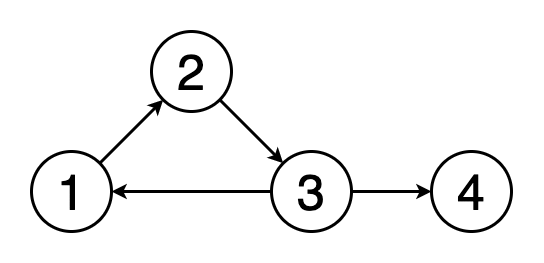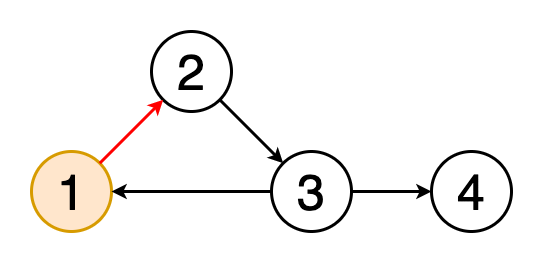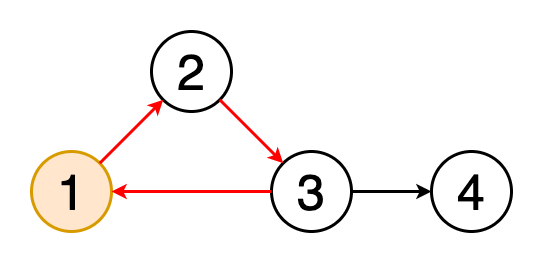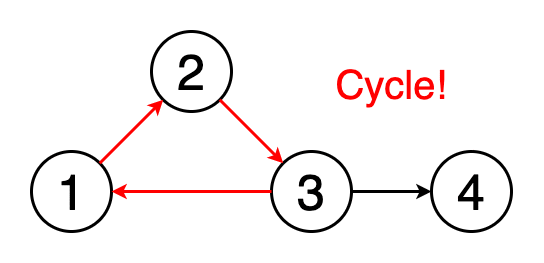
文章插图
> Fig 5. A cycle (Image by Author)
循环是图形中的第一个顶点和最后一个顶点相同的路径。如果我们从一个顶点开始，沿着一条路径行进，然后在起始顶点处结束，那么这条路径就是一个循环。循环检测是检测这些循环的过程。图5显示了遍历一个循环的动画。
演算法· 弗洛伊德循环检测算法
· 布伦特算法
应用领域· 用于基于分布式消息的算法。
· 用于在群集上使用分布式处理系统处理大规模图形。
· 用于检测并发系统中的死锁。
· 在加密应用程序中用于确定消息的密钥，该密钥可以将该消息映射到相同的加密值。
5.最小生成树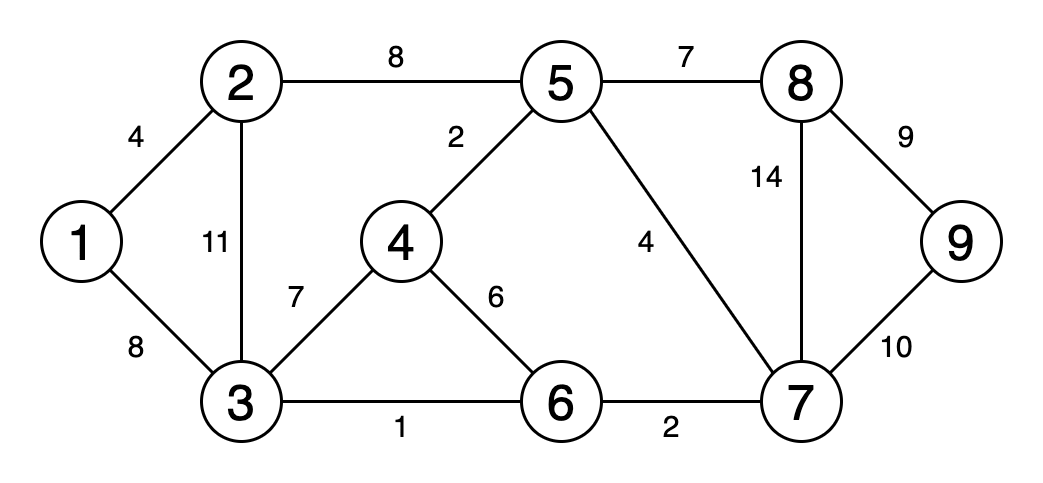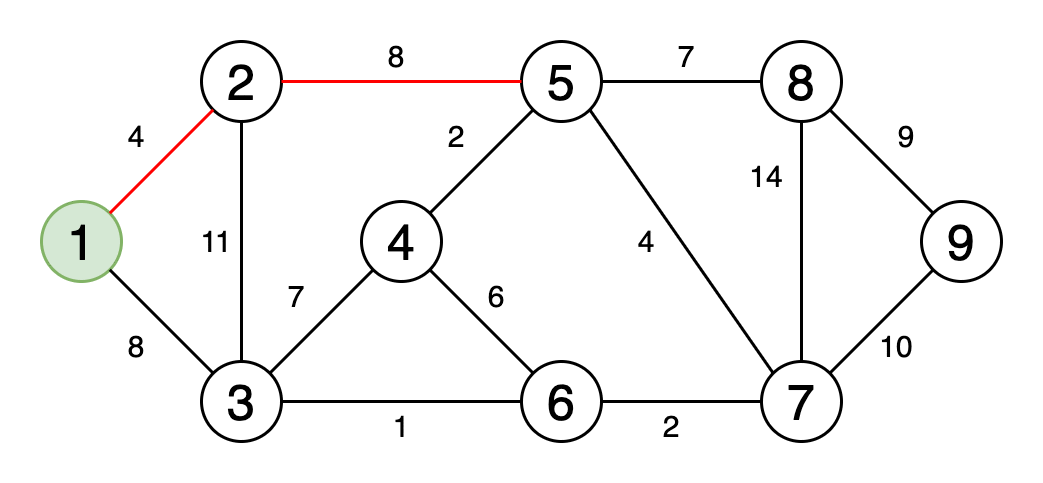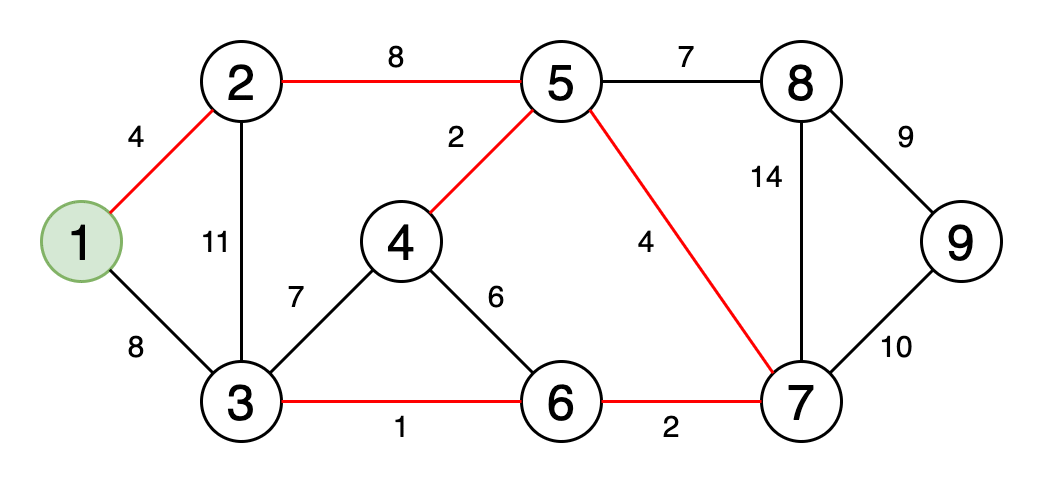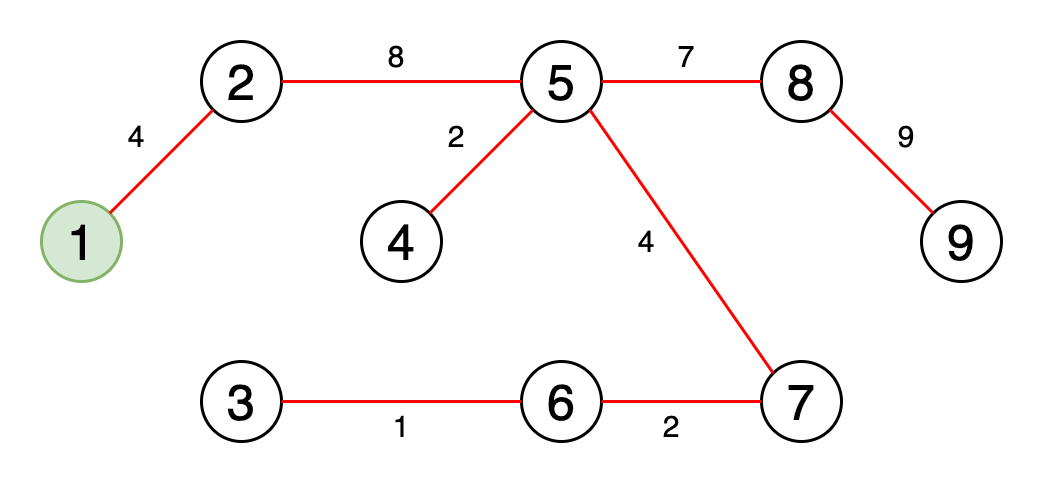
文章插图
> Fig 6. Animation showing a minimum spanning tree (Image by Author)
最小生成树是图的边缘的子集，该图以最小的边权重之和连接所有顶点，并且不包含循环。
图6是一个动画，显示了获取最小生成树的过程。
演算法· Prim的算法
· Kruskal的算法
应用领域· 用于构造树以在计算机网络中广播。
· 用于基于图的聚类分析。
· 用于图像分割。
· 用于将社会区域划分为连续区域的社会地理区域的区域化。
6.牢固连接的组件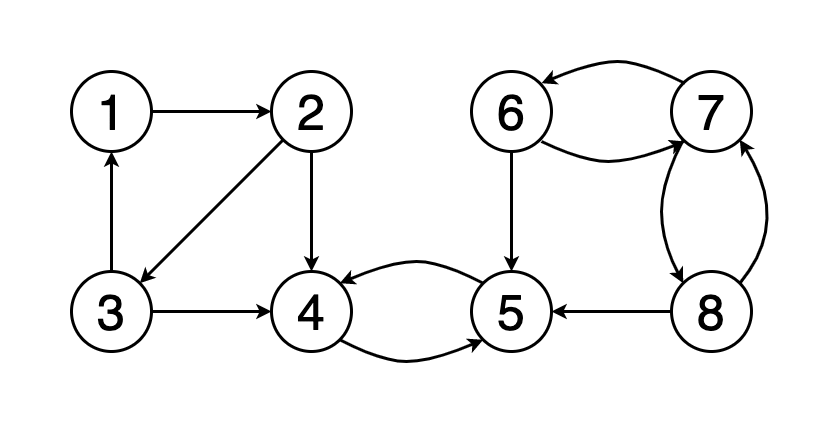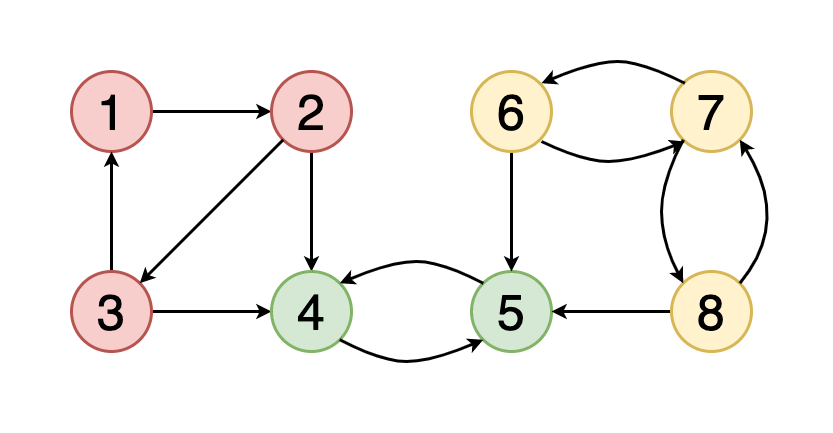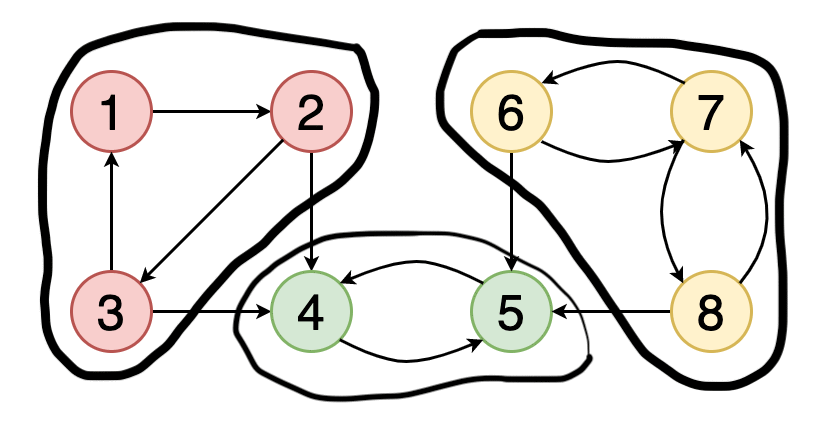
文章插图
> Fig 7. Strongly connected components (Image by Author)
如果图中的每个顶点均可从其他每个顶点到达，则称该图是牢固连接的。
图7显示了一个示例图，其中包含三个具有红色，绿色和黄色的顶点的牢固连接的组件。
演算法· Kosaraju的算法
· Tarjan的强连接组件算法
应用领域· 用于计算Dulmage–Mendelsohn分解，这是二部图边缘的分类。
· 用于社交网络中，以找到一群紧密联系并根据共同兴趣提出建议的人。
文章插图
> Image by Gerd Altmann from Pixabay
7.拓扑排序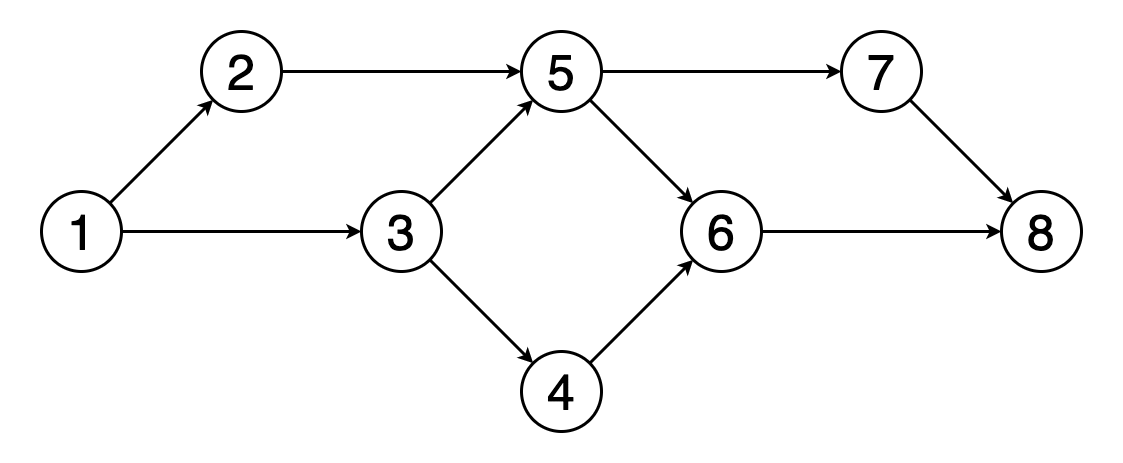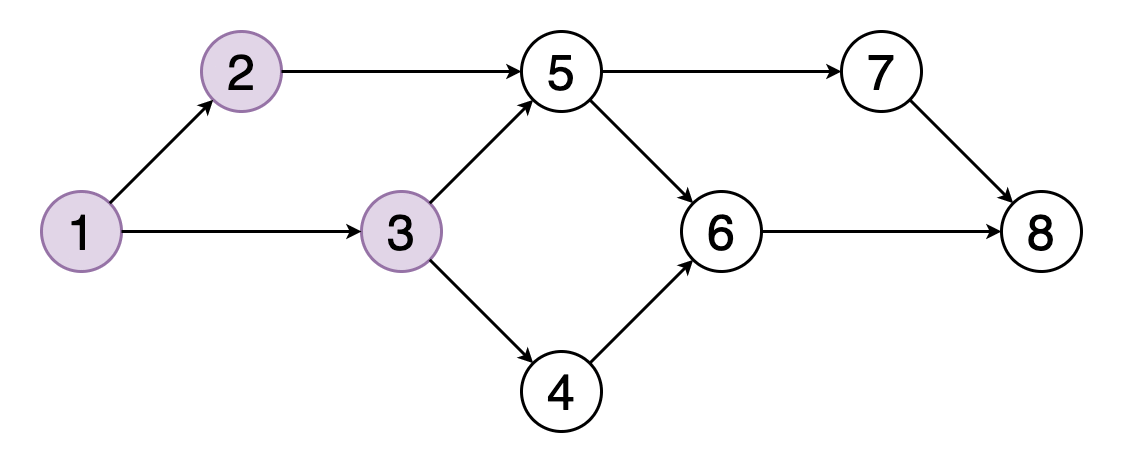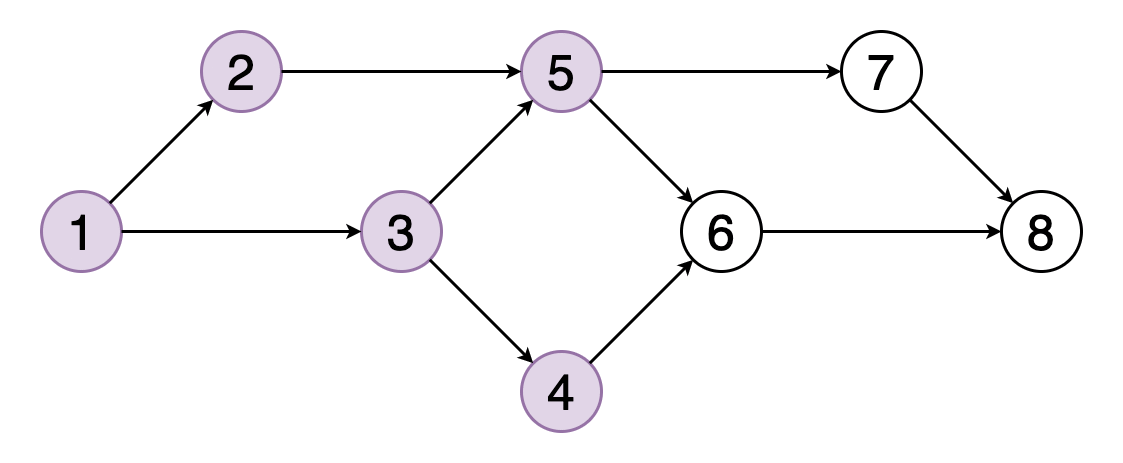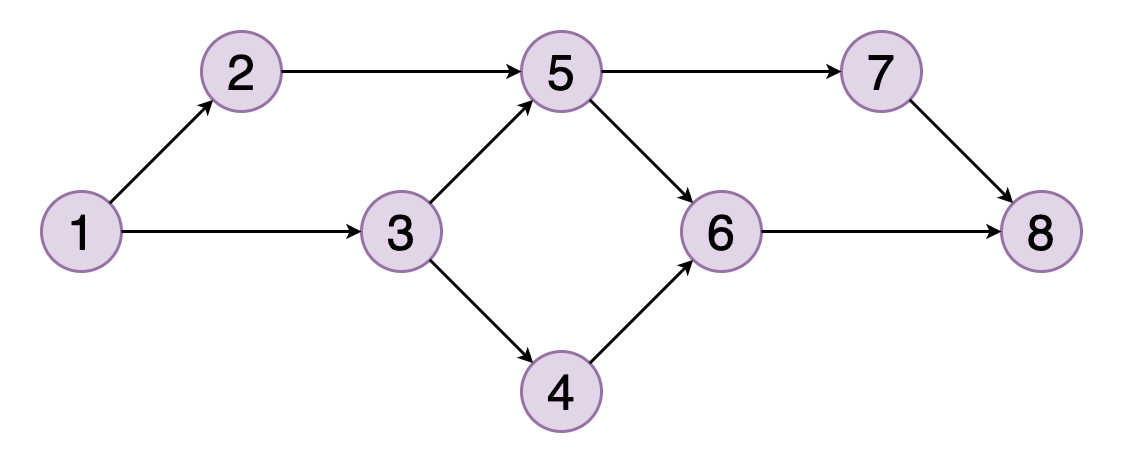
文章插图
> Fig 8. A topological ordering of vertices in a graph (Image by Author)
图的拓扑排序是其顶点的线性排序，因此对于排序中的每个有向边（u ， v），顶点u都位于v之前。
图8显示了顶点（1、2、3、5、4、6、7、8）的拓扑顺序的示例。您可以看到顶点5应该位于顶点2和3之后。类似地，顶点6应该位于顶点4和5之后。
演算法· 卡恩算法
· 基于深度优先搜索的算法
应用领域· 用于指令调度。
· 用于数据序列化。
· 用于确定在makefile中执行的编译任务的顺序。
· 用于解析链接器中的符号依赖性。
8.图形着色
文章插图
> Fig 9. Vertex colouring (Image by Author)
图形着色可在确保某些条件的同时为图形元素分配颜色。顶点着色是最常用的图形着色技术。在顶点着色中，我们尝试使用k种颜色为图形的顶点着色，并且任何两个相邻的顶点都不应具有相同的颜色。其他着色技术包括边缘着色和面部着色。