用图形解释10种图形算法快速介绍

快速介绍10种基本图形算法以及示例和可视化在现实世界中，例如社交媒体网络，网页和链接以及GPS中的位置和路线，图形已经成为一种强大的建模和捕获数据的手段。如果您有一组相互关联的对象，则可以使用图形来表示它们。
文章插图
> Image by Author
在本文中，我将简要说明10种基本图形算法，这些算法对于分析及其应用非常有用。
首先，让我们介绍一个图表。
什么是图？一个图由一组有限的顶点或节点以及一组连接这些顶点的边组成。如果两个顶点通过同一边彼此连接，则它们称为相邻顶点。
下面给出一些与图有关的基本定义。您可以参考图1的示例。
· 顺序：图形中的顶点数
· 大小：图形中的边数
· 顶点度：入射到顶点的边数
· 孤立的顶点：未连接到图中任何其他顶点的顶点
· 自环：从顶点到自身的边
· 有向图：所有边都有一个方向的图，该方向指示什么是起始顶点，什么是终止顶点
· 无向图：具有没有方向的边的图
· 加权图：图的边缘具有权重
· 未加权图形：图形的边缘没有权重
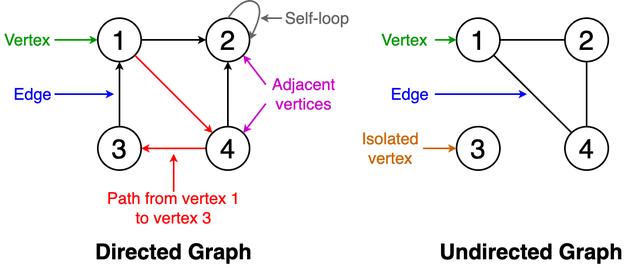文章插图
> Fig 1. Visualization of Terminology of Graphs (Image by Author)
1.广度优先搜索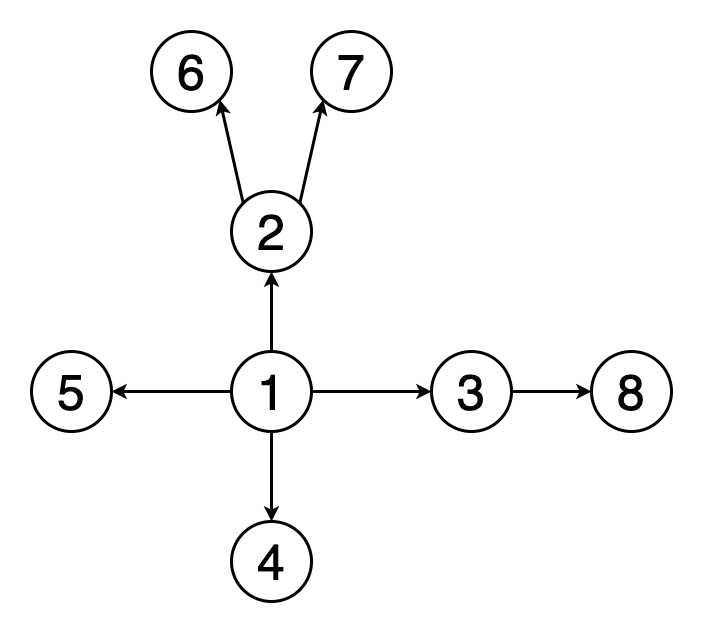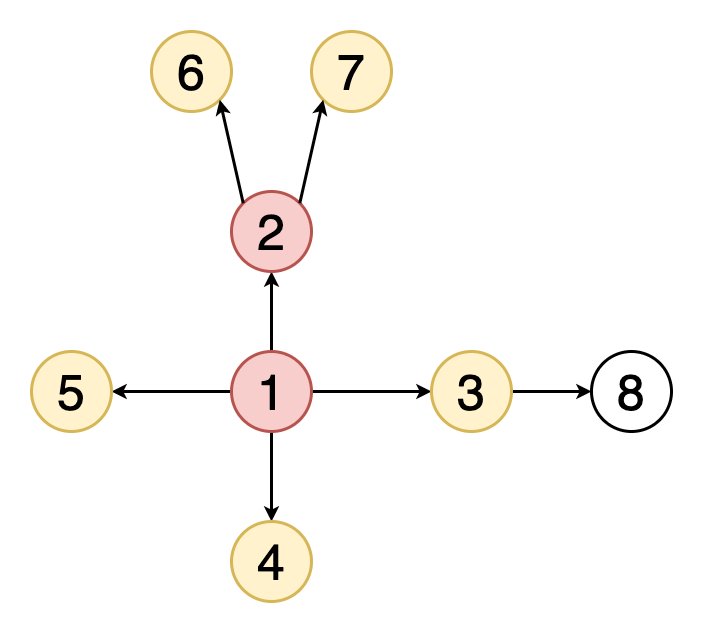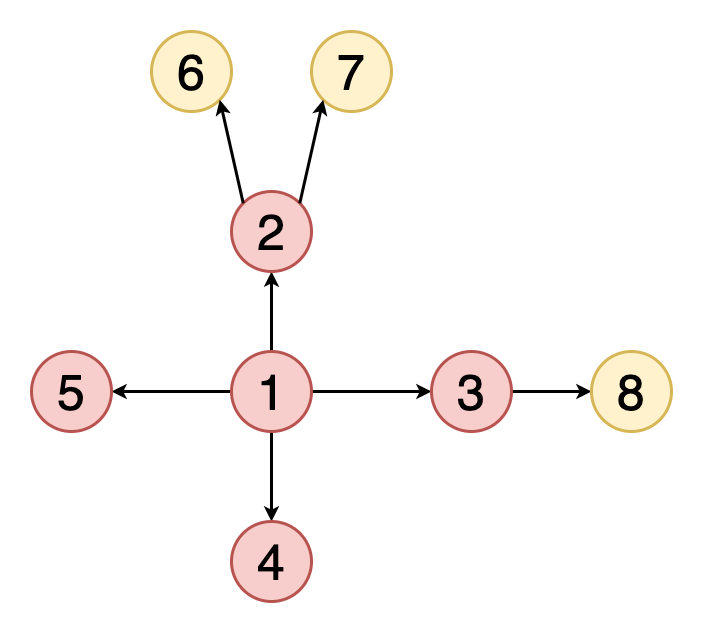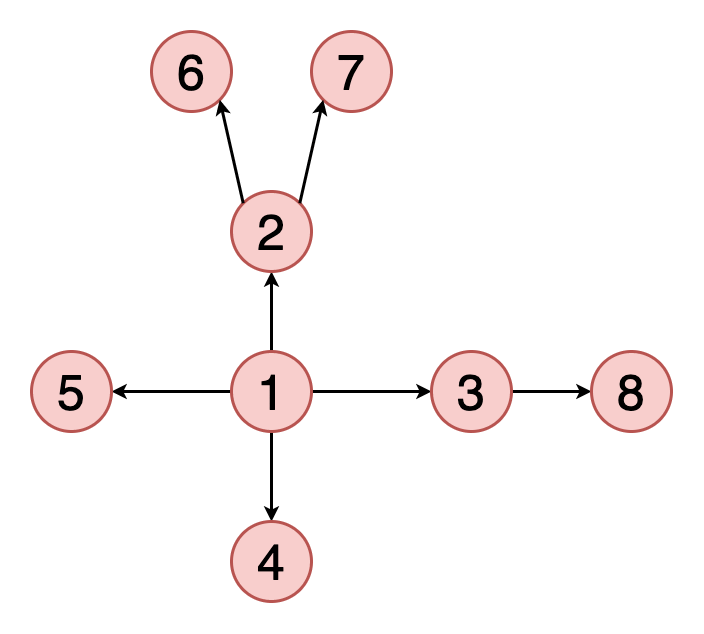
文章插图
> Fig 2. Animation of BFS traversal of a graph (Image by Author)
遍历或搜索是可以在图形上执行的基本操作之一。在广度优先搜索（BFS）中，我们从一个特定的顶点开始，并在当前深度探索其所有邻居，然后再进入下一级的顶点。与树不同，图可以包含循环（第一个顶点和最后一个顶点相同的路径）。因此，我们必须跟踪访问的顶点。在实现BFS时，我们使用队列数据结构。
图2表示示例图的BFS遍历的动画。注意如何发现顶点（黄色）并访问顶点（红色）。
应用领域· 用于确定最短路径和最小生成树。
· 搜索引擎搜寻器用来构建网页索引。
· 用于在社交网络上搜索。
· 用于查找对等网络（例如BitTorrent）中的可用邻居节点。
2.深度优先搜索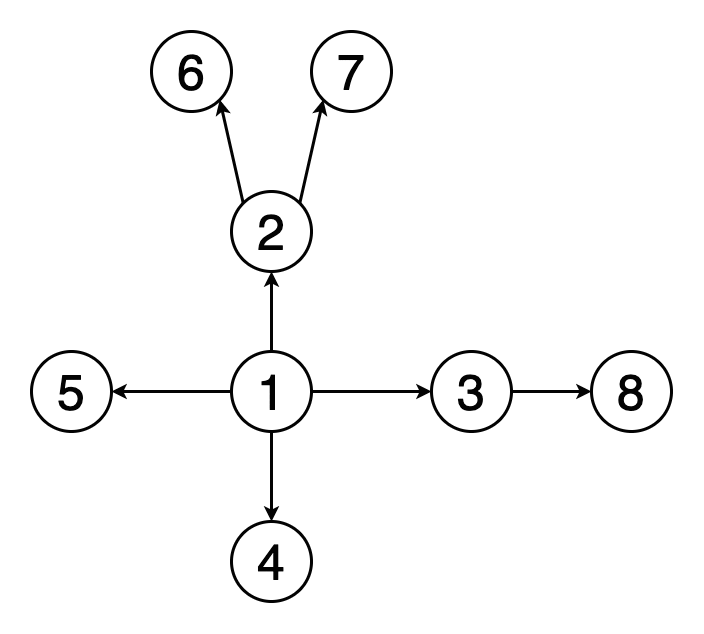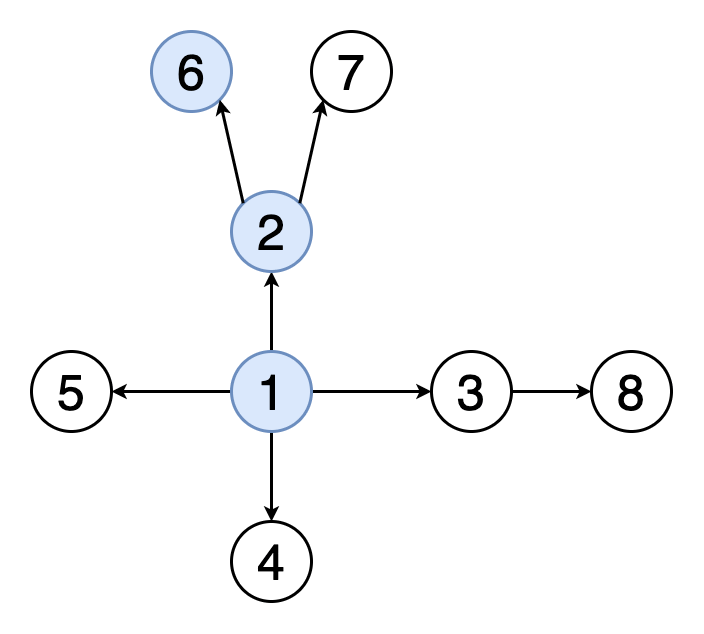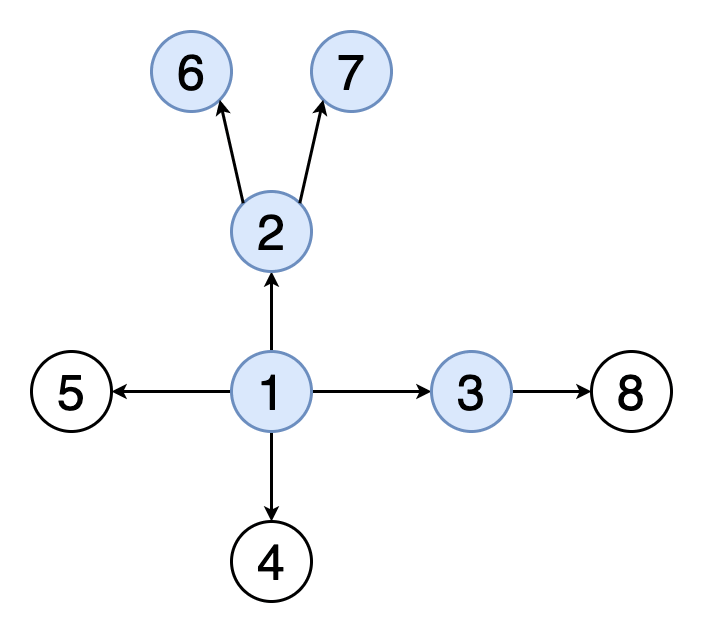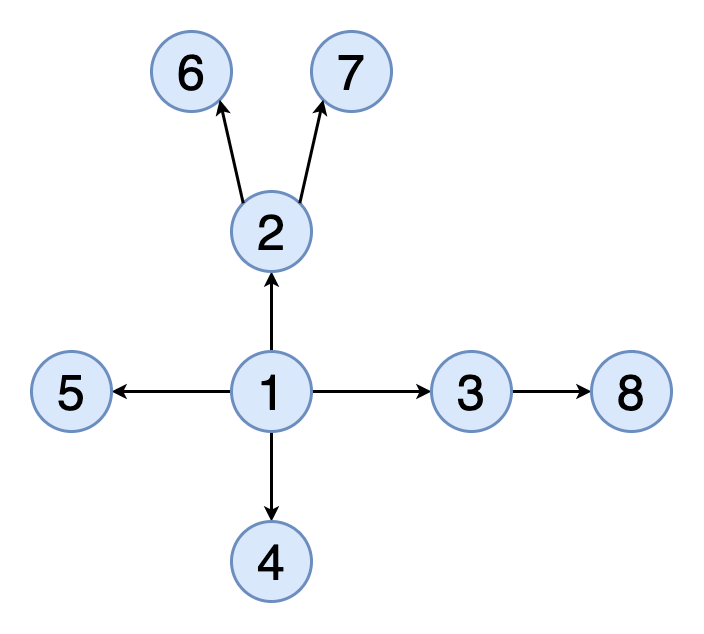
文章插图
> Fig 3. Animation of DFS traversal of a graph (Image by Author)
在深度优先搜索（DFS）中，我们从特定的顶点开始，并在回溯（回溯）之前沿每个分支进行尽可能的探索。在DFS中，我们还必须跟踪访问的顶点。在实现DFS时，我们使用堆栈数据结构来支持回溯。
图3表示与图2相同的示例图的DFS遍历的动画。请注意，它如何遍历深度和回溯。
应用领域· 用于查找两个顶点之间的路径。
· 用于检测图中的周期。
· 用于拓扑排序。
· 用于解决只有一种解决方案（例如迷宫）的难题
3.最短路径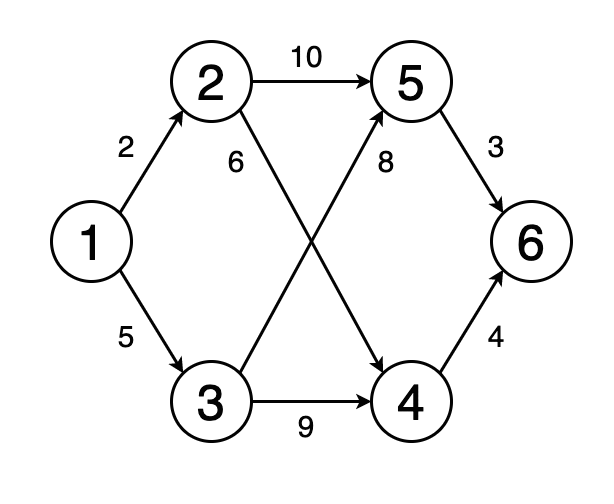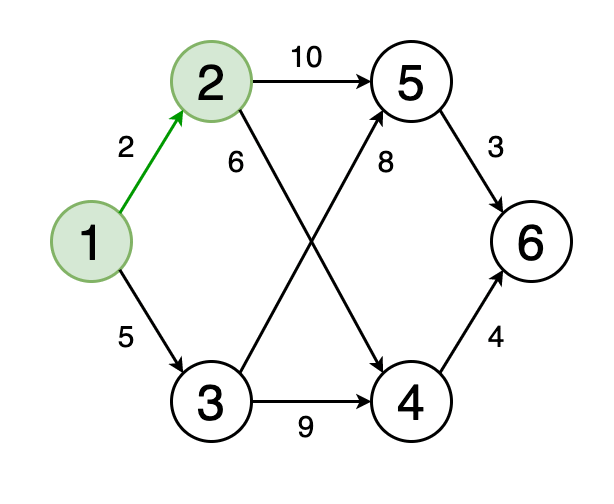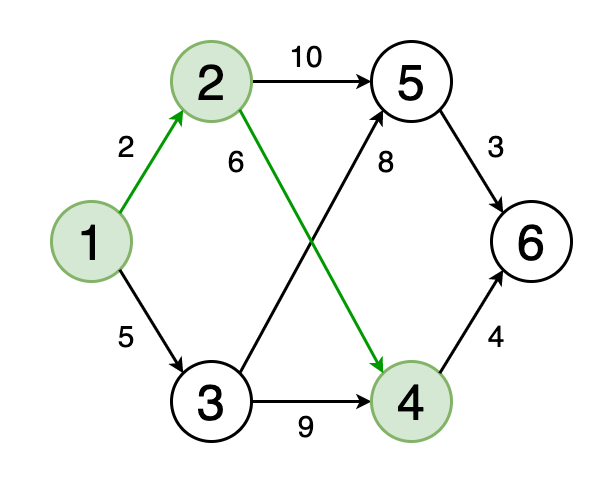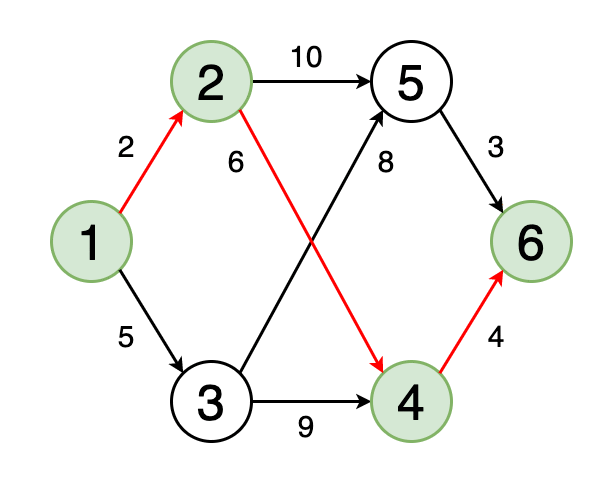
文章插图
> Fig 4. Animation showing the shortest path from vertex 1 to vertex 6 (Image by Author)
从一个顶点到另一个顶点的最短路径是图形中的一条路径，因此应移动的边的权重之和最小。
图4显示了一个动画，其中确定了图形中从顶点1到顶点6的最短路径。
演算法· Dijkstra最短路径算法
· Bellman–Ford算法
应用领域· 用于在Google地图或Apple地图等地图软件中查找从一个位置到另一个位置的路线。