硬核丨一份关于支付网络中路由问题的全面研究( 二 ) 摘要：区块链因Layer1的交易吞吐量上限

文章插图
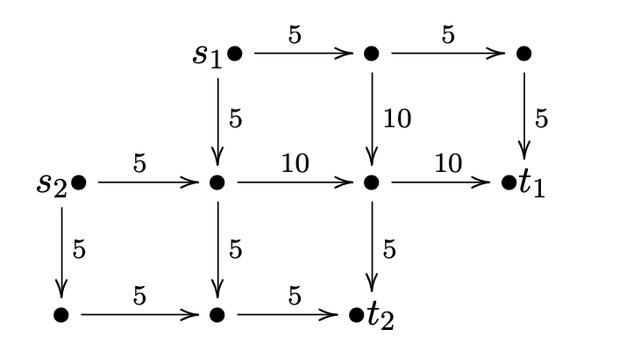
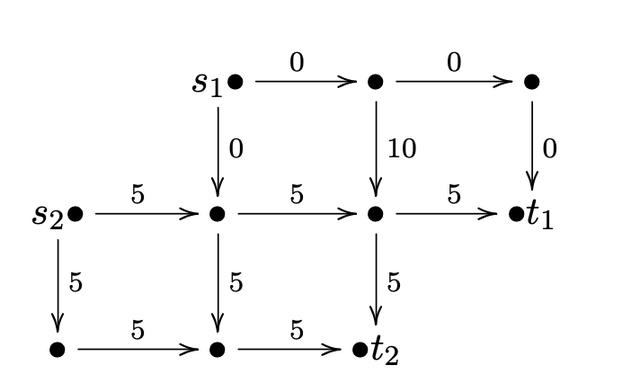
倘若把到的单位的额度全部用尽，并不只一种方案，其中一种「增广」方案使用后如下图。
文章插图
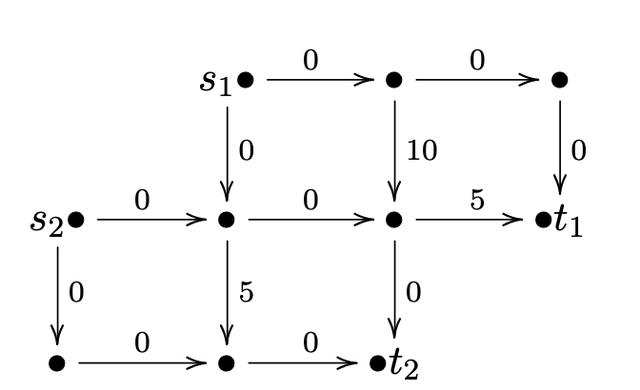
此时，到的最大流依旧为单位，不过方案唯一。如果恰好把单位流量用完，则全图残量网络如下。
文章插图
常用的最大流算法包括预留推进算法（HLPP）和一类基于增广路定理的最大流算法，其中包括了 Edmonds-Karp 算法以及他的衍生算法如 ISAP 算法和 Dinic 算法。
这些算法都具有极高的最坏情况下的理论复杂度，和往往远低于理论复杂度的可观运行效率。例如，考虑一张有节点条边的流量图， Edmonds-Karp 算法的理论计算复杂度高达， Dinic 算法的理论计算复杂度高达，而他们在正常的稀疏随机图上的执行效率很高，普通 CPU 可以在百毫秒内求出千量节点的最大流。
不难发现，对于大额支付，我们可以通过最大流算法得到两节点之间的最大可能支付额度。如果支付金额小于这个额度，我们也就通过最大流算法确立了一个支付方案。
2
基于灯塔节点的路由协议基于灯塔（landmark）节点的路由协议的总体思路如下。首先，每个节点都有资格成为灯塔节点，每个节点都有权利选择让哪些灯塔节点来协助路由。这个大前提基本保证了路由方案的去中心化特性不被打破。
然后，为了提供一定的额度隐私性并增加支付成功的概率，每一笔支付的额度被分为份，每一份由不同的灯塔节点协助完成传输。对于不分片的情况，我们认为。而灯塔协助传输的方式则是根据自己的视野为这笔金额安排一条通道，并通过与这些通道上的节点通讯获取这个通道上可以通过的最大额度。
早期方法
基于 Landmark 的路由协议思路来自于计算机网络领域的研究。其中的常见组件如下。
双向BFS寻找最短路径
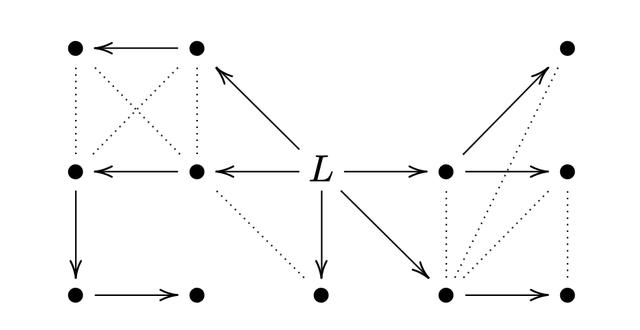
熟悉算法的读者了解，在无边权的有向图上，从单源出发的广度优先搜索（Breath-First Search, BFS）序列性质保证：BFS 树中各节点到源节点的路径，即该节点到源节点的最短路径或最短路径之一。每一个 Landmark 节点维护两棵以自己为源节点的 BFS 树，一棵基于 PCN 图，一棵基于将所有通道方向反转后的 PCN 图。当然，对于无向图而言，这两棵树是一致的。由此，对于一个从到的路由需要，先在中找到到 landmark 节点的路径，再在中找到 landmark 节点到的路径。这两个路径拼接起来，就得到了从到的一条最短路径。
文章插图
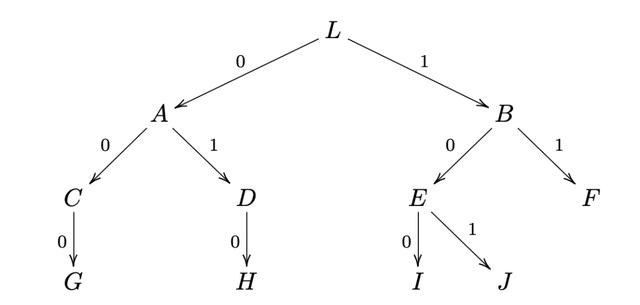
图嵌入树基图嵌入（tree-based graph embedding）让每个灯塔节点把所有的视图内的节点视为一棵树，树上的每条边对应了一条支付通道。这样，可以用一种类似 Trie 树的方式，为每个节点用从根节点到该节点的路径编号。例如下图中，节点的标号即为，节点的标号即为，节点的标号即为。当然，我们只是在用二叉树举例，现实实现中这是一颗多叉树，此时的编码范围就不再是与之间。对于叉树而言，编码范围就成了至。
文章插图
通过这样的编码方式，可以高效地确定两个节点之间的一条路径——即从付款节点到两节点的最近公共祖先（lowest common ancestor, LCA）的唯一路径拼接上从 LCA 到收款节点的唯一路径。